 . The distributed algorithm
described in this section relies on the general idea of defining
blocking guards: for each link, a blocking guard bounds the effect
connections using that link can have on other connections in the network.
. The distributed algorithm
described in this section relies on the general idea of defining
blocking guards: for each link, a blocking guard bounds the effect
connections using that link can have on other connections in the network.
As described earlier, packets that are blocked at a switch in a
Myrinet-style network not only block other packets at that particular
switch, but at upstream switches as well. Since the effect of blocked
packets is not local, admission control decisions are not easily
realizable locally . The distributed algorithm
described in this section relies on the general idea of defining
blocking guards: for each link, a blocking guard bounds the effect
connections using that link can have on other connections in the network.
. The distributed algorithm
described in this section relies on the general idea of defining
blocking guards: for each link, a blocking guard bounds the effect
connections using that link can have on other connections in the network.
Specifically, for each output Port p of a switch ![]() , we define a
blocking guard
, we define a
blocking guard ![]() , which is the longest time any packet can be
blocked at that port, be it due to either existing or future
connections anywhere in the network. For convenience, we define
, which is the longest time any packet can be
blocked at that port, be it due to either existing or future
connections anywhere in the network. For convenience, we define
![]() to be zero if no connection uses Port p of switch
to be zero if no connection uses Port p of switch ![]() .
.
For each link on the route of a newly established connection, the admission control must make sure that (i) the worst-case blocking delay of the newly established connection does not exceed the amount specified in the blocking guard, and (ii) that the new connection does not cause the worst-case blocking delay of existing connections to exceed the amount specified in the blocking guard. As connections are established and torn down, the values of the blocking guards must be modified to reflect the change in the load of the network.
In this section we describe an admission control algorithm that makes its decisions based on the values for the blocking guards and then updates their values appropriately. In Section 4 we will describe an establishment protocol based on a distributed version of this algorithm. Before we go on to describe the algorithm in detail, we define a few terms and show a number of properties.
Let ![]() be the calculated
worst-case blocking delay for packets of connection
be the calculated
worst-case blocking delay for packets of connection ![]() at Switch
at Switch
![]() . Let
. Let ![]() and
and ![]() be upper bounds on the
blocking delay other connections can cause, that branch in at
be upper bounds on the
blocking delay other connections can cause, that branch in at ![]() or
branch out at
or
branch out at ![]() , respectively. Then,
, respectively. Then,
where ![]() is the switch at which a connection
is the switch at which a connection ![]() branches in
upstream.
branches in
upstream. ![]() can then be defined by the following recurrence
relation:
can then be defined by the following recurrence
relation:
![]()
![]()
The following theorem shows that ![]() is an upper bound for
is an upper bound for
![]() .
.
Our algorithm does not make use of ![]() directly, but of
the related value
directly, but of
the related value ![]() which we call the
guard-based calculated worst-case blocking delay for packets of
connection
which we call the
guard-based calculated worst-case blocking delay for packets of
connection ![]() at Switch
at Switch ![]() . If the upper bound
. If the upper bound ![]() on
on
![]() is defined as follows
is defined as follows
we can define ![]() by the following recurrence relation:
by the following recurrence relation:
![]()
![]()
The following observation shows that ![]() is a safe
approximation for
is a safe
approximation for ![]() , and, hence, for
, and, hence, for ![]() . It is
the basis for our algorithm.
. It is
the basis for our algorithm.
The following theorem states that, at any switch, it is sufficient to check the guard-based calculated worst-case blocking delay of the new connection against the blocking guard at the same switch to see whether any existing connection may miss its deadline.
Given a set of established connections, the following three-step
admission control algorithm determines whether a newly arriving
connection ![]() can be established along the route
can be established along the route ![]() . The algorithm rejects the new connection if
(i) the performance requirements of
. The algorithm rejects the new connection if
(i) the performance requirements of ![]() can not be satisfied, or (ii)
if the performance requirements of existing connections would be
violated by accepting
can not be satisfied, or (ii)
if the performance requirements of existing connections would be
violated by accepting ![]() . If
. If ![]() is accepted, the blocking
guards along its route are updated appropriately.
is accepted, the blocking
guards along its route are updated appropriately.
Step 1: The guard-based worst-case blocking time
![]() for packets of the new
connection is determined for each switch
for packets of the new
connection is determined for each switch ![]() along the route of
along the route of ![]() . If at any switch
. If at any switch ![]() the blocking guard
the blocking guard ![]() is exceeded,
that is, if
is exceeded,
that is, if ![]() , establishing the new connection
may violate the requirements of an existing
connection, and the new connection
, establishing the new connection
may violate the requirements of an existing
connection, and the new connection ![]() is
rejected.
is
rejected.
Step 2: If no blocking guard is exceeded, the algorithm
proceeds to the final acceptance test at the
source. The guard-based calculated blocking time
![]() at the entrance to the network
is compared to the deadline requirements, i.e.,
it is checked whether
at the entrance to the network
is compared to the deadline requirements, i.e.,
it is checked whether ![]() .
If this is not the case, packets of
.
If this is not the case, packets of ![]() may not
meet their delay requirements, and the connection
is rejected.
may not
meet their delay requirements, and the connection
is rejected.
Step 3: After the new connection ![]() has been accepted
by the source, the blocking guards at the outgoing
ports on the route of
has been accepted
by the source, the blocking guards at the outgoing
ports on the route of ![]() must be updated to
reflect the acceptance of
must be updated to
reflect the acceptance of ![]() . Specifically,
they may need to be reduced to prevent future
connection admissions from violating
. Specifically,
they may need to be reduced to prevent future
connection admissions from violating ![]() 's
performance guarantees.
's
performance guarantees.
If ![]() is the new value for
is the new value for ![]() after the acceptance
of
after the acceptance
of ![]() , the following two conditions must be satisfied for the
blocking guards to remain valid after the connection has been
established:
, the following two conditions must be satisfied for the
blocking guards to remain valid after the connection has been
established:
The following set of formulae can be shown to generate a set of
updated blocking guards that satisfy the above conditions:
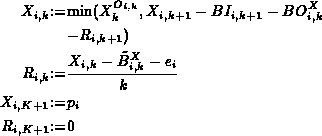
![]()
where BI and ![]() have been defined earlier.
have been defined earlier.
Intuitively, the term ![]() gives an indication of how much
additional blocking can be accepted at output Port
gives an indication of how much
additional blocking can be accepted at output Port ![]() in the
future, without violating the blocking guard
in the
future, without violating the blocking guard ![]() at the
previous switch
at the
previous switch
![]() . We call
. We call ![]() the local residual time between the two
ports. Updating the blocking guards means allocating residual time to
links along the route of the new connection.
the local residual time between the two
ports. Updating the blocking guards means allocating residual time to
links along the route of the new connection.
The above formula trivially satisfies Condition 1. We show in [12]
that the formula satisfies Condition 2 as well.
The correctness of the admission control algorithm follows directly
from the above theorems: On one side, it never accepts a connection
whose packets may miss their deadlines. This is enforced by the
acceptance test at the source. On the other side, the admission
control algorithm never accepts a connection if this may cause packets
of existing connections to miss their deadlines. This is enforced by
comparing an upper bound on the blocking delay ( ![]() ) with
blocking guards at the intermediate switches. Theorem 2
states that this test is sufficient. We show in [12]
that the algorithm updates the blocking guards correctly to
reflect the acceptance of
) with
blocking guards at the intermediate switches. Theorem 2
states that this test is sufficient. We show in [12]
that the algorithm updates the blocking guards correctly to
reflect the acceptance of ![]() .
.