In the following, we assume a Myrinet network of general topology, consisting of hosts and switches and pairs of unidirectional links. The links forward arbitrary-length packets, which are routed through the switches in wormhole manner. As reflected by the name, the process of routing and transmission of a packet is like the movement of a worm. Whenever the header of a packet reaches a switch, the remaining portion of the packet is forwarded to the desired outgoing port (if available) as soon as the header is decoded, without waiting for the entire packet to reach the switch. Longer packets can therefore extend over several switches. If the desired outgoing port is not available because it is being used for the transmission of another packet, the header of the packet blocks.
Myrinet switches are perfect, meaning that packets do not conflict at a switch unless they are directed to the same outgoing link. There may be as many packets simultaneously traversing the switch as there are outgoing links. If more than one packet must wait, they are served in round-robin manner.
A simple hop-by-hop STOP/GO flow control mechanism (which acts as backpressure flow control) ensures that a packet blocked at a switch blocks at the upstream switches as well. Since only a small buffer is associated with input ports at each switch, the packet can easily be blocked up to the sender.
In order to streamline the packet processing at switches, source routing is used. A source host determines the route to a destination (a list of switches and output ports) and places it into the header of the packet. When the header arrives at the switch, the router reads the information and determines the desired outgoing port. Then it is forwarded through the specified output port to the next switch.
In conjunction with its flexible point-to-point topology, this results
in a low-cost but scalable networking technology that provides
guaranteed delivery of packets at very high speed and low latency.
Figure 1 shows a snapshot of a wormhole network with
a number of packets in traffic. In this example, the network consists
of six hosts 
, which are connected by nine
switches 
, forming a mesh.
Figure 1: Network with Packets in Transit
In this example, Packet 
is being blocked on the link between
and 
by Packet 
. Packets 
and , on the
other side, do not affect each other, although they use the same
switch 
. This example illustrates also how a packet can be
indirectly blocked by another packet: although and 
do not
directly contend for a link, indirectly blocks by blocking
, which in turn blocks on the link from to .
Once the head of the packet reaches the destination, the remainder can
be sent at potentially full link bandwidth (of 640 Mb/s or 1.28Gb/s in
the case of Myrinet). In order to bound packet delivery delay due to
blocking during path setup, however, proper connection acceptance and
connection management strategies must be devised. In the following,
we assume that connections adhere to a periodic traffic specification.
Each connection is of type 
, where 
specifies the route followed by packets of 
, 
defines the
worst-case message length (in terms of transmission time), and 
specifies the worst-case interarrival time of packets of .
We assume without loss of generality that the packets of Connection
enter the network at Switch 
and are routed along the
sequence of switches 
. For convenience we call the sender host 
and the
receiver host 
. Assuming a round-robin service policy in the
switches, we can determine the worst-case blocking time
experienced by a packet of connection because of
contention for the outgoing link at Switch 
.
The worst case happens when all packets contending for the same output
link at arrive just before the packet of . All these
packets may in turn be blocked at downstream switches. The worst-case
blocking delay at Switch can therefore be defined by
the following recurrence relation:
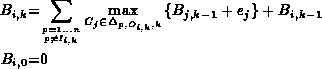
In the above recurrence relation n is the number of ports of Switch
; 
and 
are the input and output port,
respectively, of Connection at Switch ;
denotes the set of connections that use Port p as
input port and Port q as output port at Switch . To simplify
the notation, in the following we will generally omit the index k for
if it can be deduced from the context.
We say that a connection 
branches in with at Switch
if the two connections use different input ports but share the
same output port at Switch . Using the notation above: 
and 
. The set of all connections
branching in at with at Switch is denoted by 
.
Similarly, a connection is said to branch out from at
Switch if the two connections share the input port but have
different output ports at , i.e., 
, but
. The set of all connections branching out from
at is denoted by 
.
Relation( 1) allows for a very simple (though expensive!)
centralized admission control scheme. With our simple periodic
traffic model we can use the following formula to test whether packets
of connection can successfully be delivered before the end of
the period:
that is, whether for all connections the worst-case blocking time at their entry to the network plus the transmission time does not exceed the period.
For a new connection to be accepted, we centrally determine whether (i) the timing requirements of the new connection can be satisfied and whether (ii) the timing requirements of existing connections are not violated. Since the admission of a new connection can potentially affect all previously established connections, the cost of this operation grows quadratically with the number of accepted connections. Computationally less demanding methods must be devised, in particular for systems with connections that are dynamically established and torn down.
In the following section, we describe a fully distributed admission control scheme that has a time overhead that grows linearly with the diameter of the network.