6 Subsystem Codes
Subsystem codes were recently introduced in an effort to unify quantum
error-correcting codes, decoherence free subspaces, and noiseless subsystems. A
subsystem code 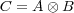 is a subspace of a finite-dimensional Hilbert space that
is decomposed into a tensor product of two vector spaces
is a subspace of a finite-dimensional Hilbert space that
is decomposed into a tensor product of two vector spaces 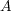 and
and 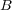 , respectively
called the subsystem
, respectively
called the subsystem 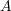 and the co-subsystem
and the co-subsystem 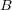 . The main idea is that the
information is encoded in the subsystem
. The main idea is that the
information is encoded in the subsystem 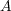 and that all errors affecting the
co-subsystem
and that all errors affecting the
co-subsystem 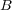 are ignored.
are ignored.
Clifford codes are the most natural way to construct subsystem codes
such that 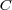 is a stabilizer code, the dimensions of
is a stabilizer code, the dimensions of 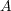 and
and 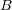 can be
controlled, and the set of detectable errors can be determined.
can be
controlled, and the set of detectable errors can be determined.
One of our key results is that any additive classical error-correcting codes yields a subsystem code, no self-orthogonality is needed!
- A. Klappenecker and P.K. Sarvepalli. Clifford code construction of
operator quantum error correcting codes. quant-ph/0604161, April
2006
@Unpublished{pre0604,
author = {Klappenecker, A. and Sarvepalli, P.K.},
title = {Clifford code construction of operator quantum error correcting codes},
note = {quant-ph/0604161},
month = {April},
year = 2006
}


