2 Nice Error Bases
A quantum error-correcting codes must be able to deal with a continuum of errors.
However, quantum mechanics is linear; hence, it suffices to consider a discrete set of
errors. A convenient choice for such a set of error is given by a nice error basis. A nice
error basis 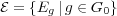 is a set of unitary
is a set of unitary 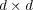 matrices indexed by a finite
group
matrices indexed by a finite
group 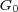 of order
of order 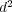 such that
such that
- 1.
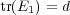 for the element of
for the element of 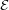 indexed by the identity element of
indexed by the identity element of 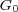 ;
;
- 2.
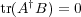 for distinct
for distinct 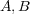 in
in 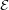 ;
;
- 3.
- a scalar multiple of the product
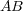 is in
is in 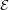 for all
for all 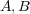 in
in 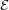 .
.
In particular, the matrices of a nice error basis form an orthonormal basis with
respect to the trace inner product 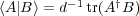 , a very valuable
property.
, a very valuable
property.
- A. Klappenecker and M. Rötteler. Nice error bases: Constructions,
equivalence, and applications. In M. Fossorier, T. Hoeholdt, and A. Poli,
editors, Applied Algebra, Algebraic Algorithms, and Error Correcting Codes –
15th International Symposium, AAECC-15, Toulouse, France, May 12-16,
2003, Proceedings, volume 2643 of LNCS, pages 139–149. Springer-Verlag,
2003
@InProceedings{klappenecker038,
author = {Klappenecker, A. and R{\"o}tteler, M.},
title = {Nice error bases: {C}onstructions, equivalence, and applications},
booktitle = {Applied Algebra, Algebraic Algorithms, and Error Correcting Codes --
15th International Symposium, AAECC-15, Toulouse, France,
May 12-16, 2003, Proceedings},
pages = {139-149},
year = 2003,
editor = {Fossorier, M. and Hoeholdt, T. and Poli, A.},
volume = 2643,
series = {LNCS},
publisher = {Springer-Verlag}
} - A. Klappenecker and M. Rötteler. On the monomiality of nice error bases.
IEEE Trans. Inform. Theory, 51(3):1084–1089, 2005
@Article{klappenecker048,
author = {Klappenecker, A. and R{\"o}tteler, M.},
title = {On the Monomiality of Nice Error Bases},
journal = {IEEE Trans. Inform. Theory},
year = 2005,
volume = 51,
number = 3,
pages = {1084-1089}
}


