4 Clifford Codes
A fundamental problem is to decide when a Clifford codes is not equal to a stabilizer
code. If we are given a Clifford code defined by 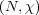 with nonabelian normal
subgroup
with nonabelian normal
subgroup 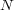 of
of 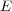 , there might exist an abelian normal subgroup
, there might exist an abelian normal subgroup 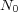 of
of
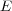 and a one-dimensional character of
and a one-dimensional character of 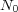 so that the two codes are the
same,
so that the two codes are the
same,
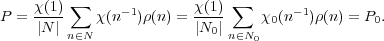
- A. Klappenecker and M. Rötteler. Remarks on Clifford codes. In
IEEE International Symposium on Information Theory, page 354,
2004
@InProceedings{klappenecker044,
author = {Klappenecker, A. and R{\"o}tteler, M.},
title = {Remarks on {C}lifford Codes},
booktitle = {IEEE International Symposium on Information Theory},
pages = {354},
year = {2004}
} - A. Klappenecker and M. Rötteler. On the structure of nonstabilizer
Clifford codes. Quantum Information and Computation, 4(2):152–160,
2004
@Article{klappenecker045,
author = {Klappenecker, A. and R\"otteler, M.},
title = {On the Structure of Nonstabilizer {C}lifford Codes},
journal = {Quantum Information and Computation},
year = 2004,
volume = 4,
number = 2,
pages = {152-160}
}


