1 Introduction
A quantum error control code is a subspace  of a the ambient state space
of a the ambient state space
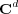 . We usually want more structure to simplify the search for good quantum
codes and to ease the design of encoding algorithms. The first conceptual
simplification is done by introducing an abstract error group
. We usually want more structure to simplify the search for good quantum
codes and to ease the design of encoding algorithms. The first conceptual
simplification is done by introducing an abstract error group 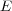 , a finite
group with a representation of unitary
, a finite
group with a representation of unitary 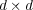 matrices that allows one to
express an arbitrary error as a linear combination of the representing matrices
of
matrices that allows one to
express an arbitrary error as a linear combination of the representing matrices
of 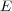 .
.
We exploit the group structure of an abstract error group 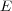 to define quantum
codes. Let
to define quantum
codes. Let 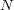 be a normal subgroup of
be a normal subgroup of 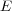 and
and 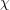 an irreducible character of
an irreducible character of 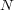 .
A Clifford code (or better Knill code) for
.
A Clifford code (or better Knill code) for 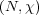 is a subspace of
is a subspace of 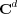 that is
given by the image of an orthogonal projector
that is
given by the image of an orthogonal projector
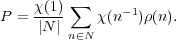 | (1) |
The definition allows one to elegantly describe the detectable errors in representation theoretic terms, as was noted by Knill. In principle, it is thus possible to compute the most important parameters of the code, but it is computationally too hard in many cases.
A special case of this definition is of particular interest. If 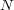 is an abelian
normal subgroup of
is an abelian
normal subgroup of 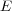 and
and 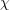 an irreducible character, then (1) is said to
define a stabilizer code. A nonzero stabilizer code is then a joint eigenspace
an irreducible character, then (1) is said to
define a stabilizer code. A nonzero stabilizer code is then a joint eigenspace
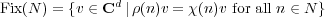 .
.

