
Due Wednesday 4/8 Monday 4/13 at 11:59 pm. You must work individually.
In this assignment, you will be writing a ray tracer. You will be implementing Blinn-Phong shading with multiple lights, shadows, reflections, and optionally refraction.

The skeleton code for Assignment 1 is a good starting point. Just like A1, this assignment does not use OpenGL and instead writes the result as an image file. You may also reuse any of your previous code from this course for this assignment.
The command line argument should be:
> ./A5 <SCENE> <IMAGE WIDTH> <IMAGE HEIGHT> <IMAGE FILENAME><SCENE>: Scene description number from 1 to 4, described below.<IMAGE WIDTH>: Width of the resulting image, e.g., 1024<IMAGE HEIGHT>: Height of the resulting image, e.g., 1024<IMAGE FILENAME>: Output filename, e.g., output.png.Set up the camera manually with the following parameters:
(0, 0, 5)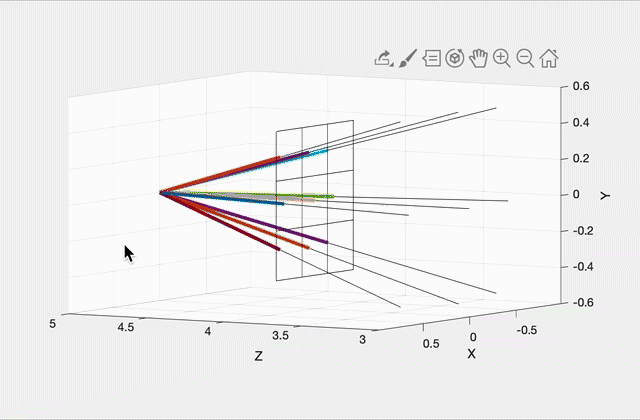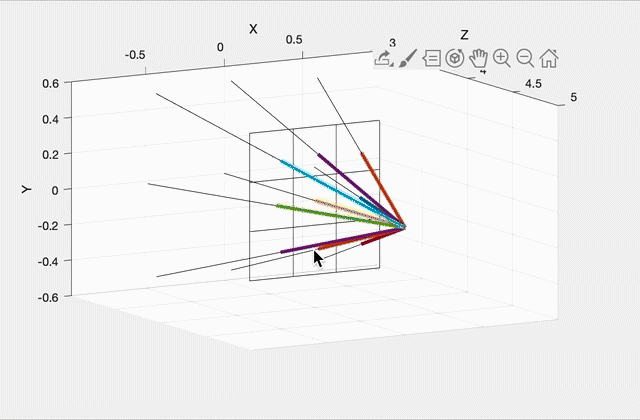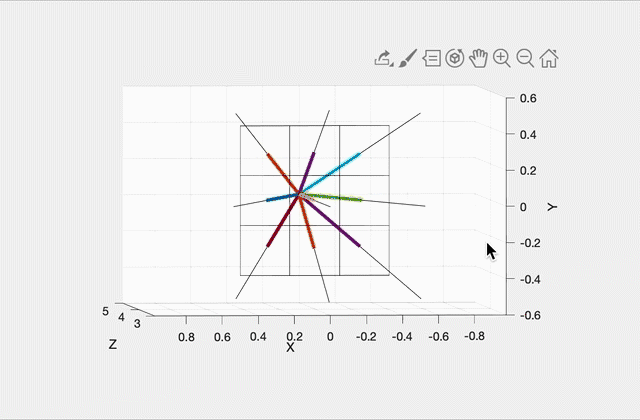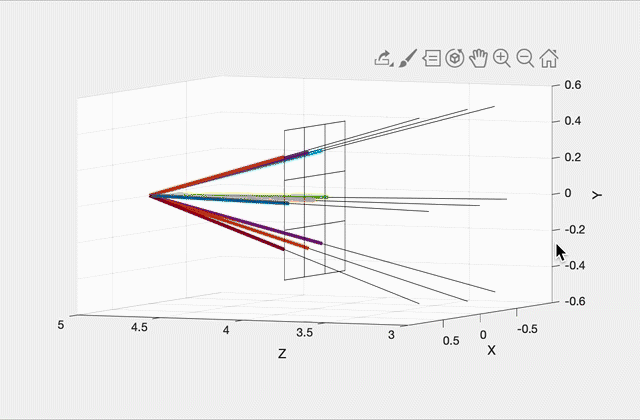

Imagine a virtual plane at Z=4.0 (i.e., one unit away from the camera, which is at Z=5.0). Our virtual rays will be starting at (0, 0, 5) and then will be going through the center of each pixel in the virtual plane. For example, in the left image, there will be 9 rays, including one going straight out through the center of the middle pixel. The right image shows how these rays would look for a 10 by 10 image. (This was rendered with OpenGL for pedagogical purposes. Your code does not need to show the virtual scene in 3D.)
To start, write a function that can generate these rays given the camera specifications above, and the width and height of the output image from the commandline argument. With a 3x3 image, the 9 rays should have the following directions (each column is a unit direction vector):
0.2572 0.0000 -0.2572 0.2662 0.0000 -0.2662 0.2572 0.0000 -0.2572
0.2572 0.2662 0.2572 0.0000 0.0000 0.0000 -0.2572 -0.2662 -0.2572
-0.9315 -0.9639 -0.9315 -0.9639 -1.0000 -0.9639 -0.9315 -0.9639 -0.9315(Click here for a screenshot of the data in case your screen is too small.) Since the camera is not rotated, the middle ray’s direction is (0, 0, -1), straight ahead along the negative Z direction.
Your first scene will consist of three spheres and one light.
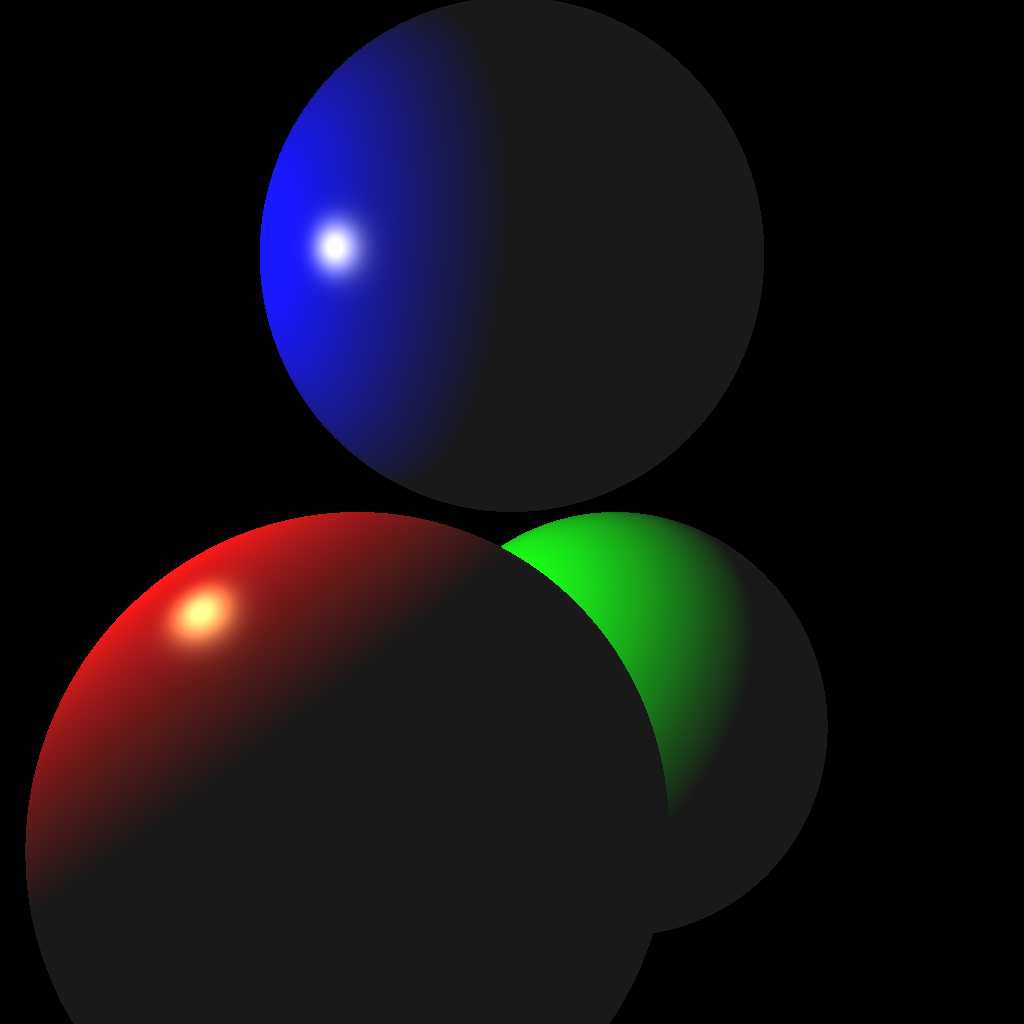
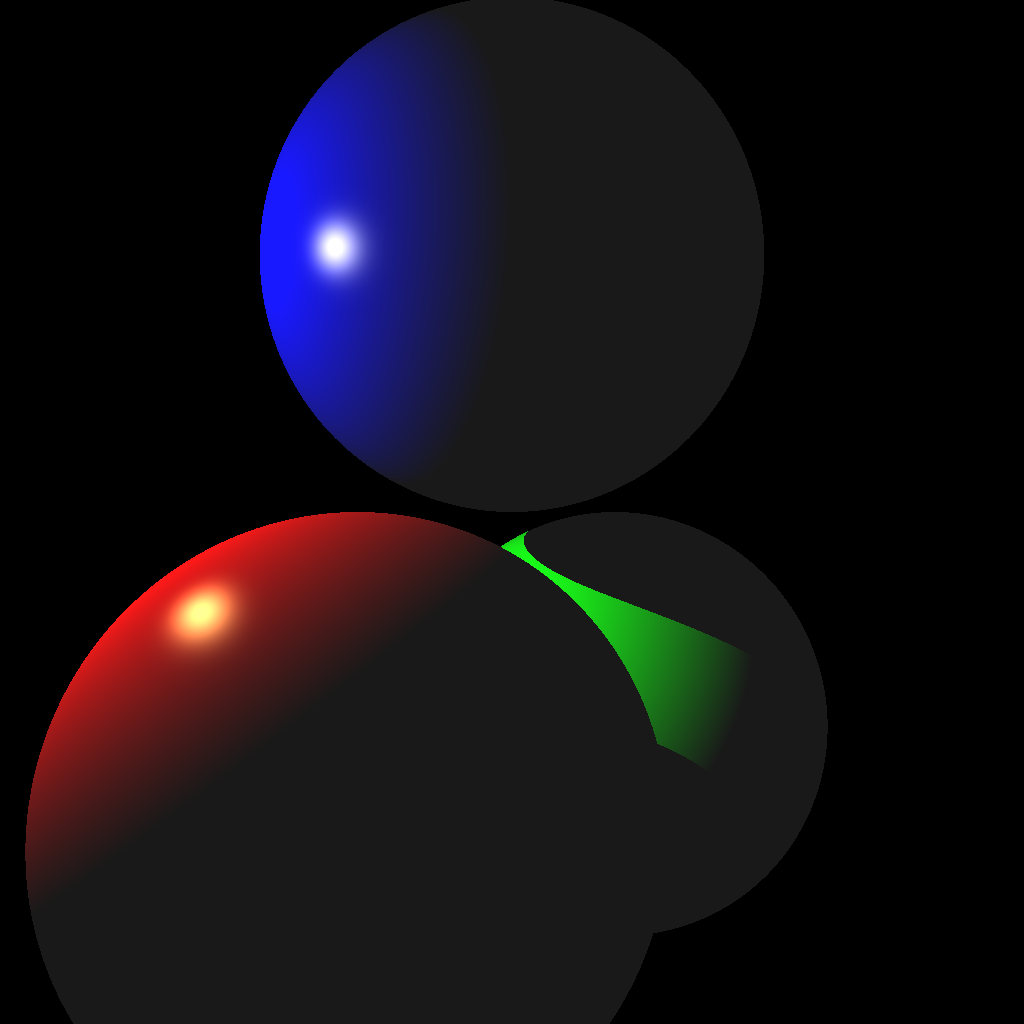
(Left) Without shadows. (Right) With shadows.
To create the scene, you can hard code the values in your code. (You may also use a parser if you prefer.) These values must be used when the command line argument <SCENE> is set to 1. Make sure to use exactly these values, since they will be used to test your code with an automatic script.
Light
(-2.0, 1.0, 1.0)1.0Red Sphere
(-0.5, -1.0, 1.0)(1.0, 1.0, 1.0)(1.0, 0.0, 0.0)(1.0, 1.0, 0.5)(0.1, 0.1, 0.1)100.0Green Sphere
(0.5, -1.0, -1.0)(1.0, 1.0, 1.0)(0.0, 1.0, 0.0)(1.0, 1.0, 0.5)(0.1, 0.1, 0.1)100.0Blue Sphere
(0.0, 1.0, 0.0)(1.0, 1.0, 1.0)(0.0, 0.0, 1.0)(1.0, 1.0, 0.5)(0.1, 0.1, 0.1)100.0I highly recommend writing test cases for the collision functions. For example, place a unit-radius sphere at the origin and shoot a ray from (0, 0, 5) with direction (0, 0, -1). The ray should hit the sphere at (0, 0, 1) and (0, 0, -1). Try other test cases, with a different radius and/or position, as well as different rays. You may use downloaded code for collision detection, but if you do, you must cite it in your README.
Once your intersection functions have been tested, you’re ready to start implementing a ray tracer. First, shoot just the primary view rays and not the shadow rays (left image above). Once you get the correct result, add the shadow rays (right image above).
Your code should be efficient enough to generate a 1024 by 1024 image without having to wait a long time. It should only take a few seconds at most, even on an older computer. If your code is slow, make sure you are not passing big STL vectors by value and that you are running your code in release mode. Excessively slow code will be penalized.
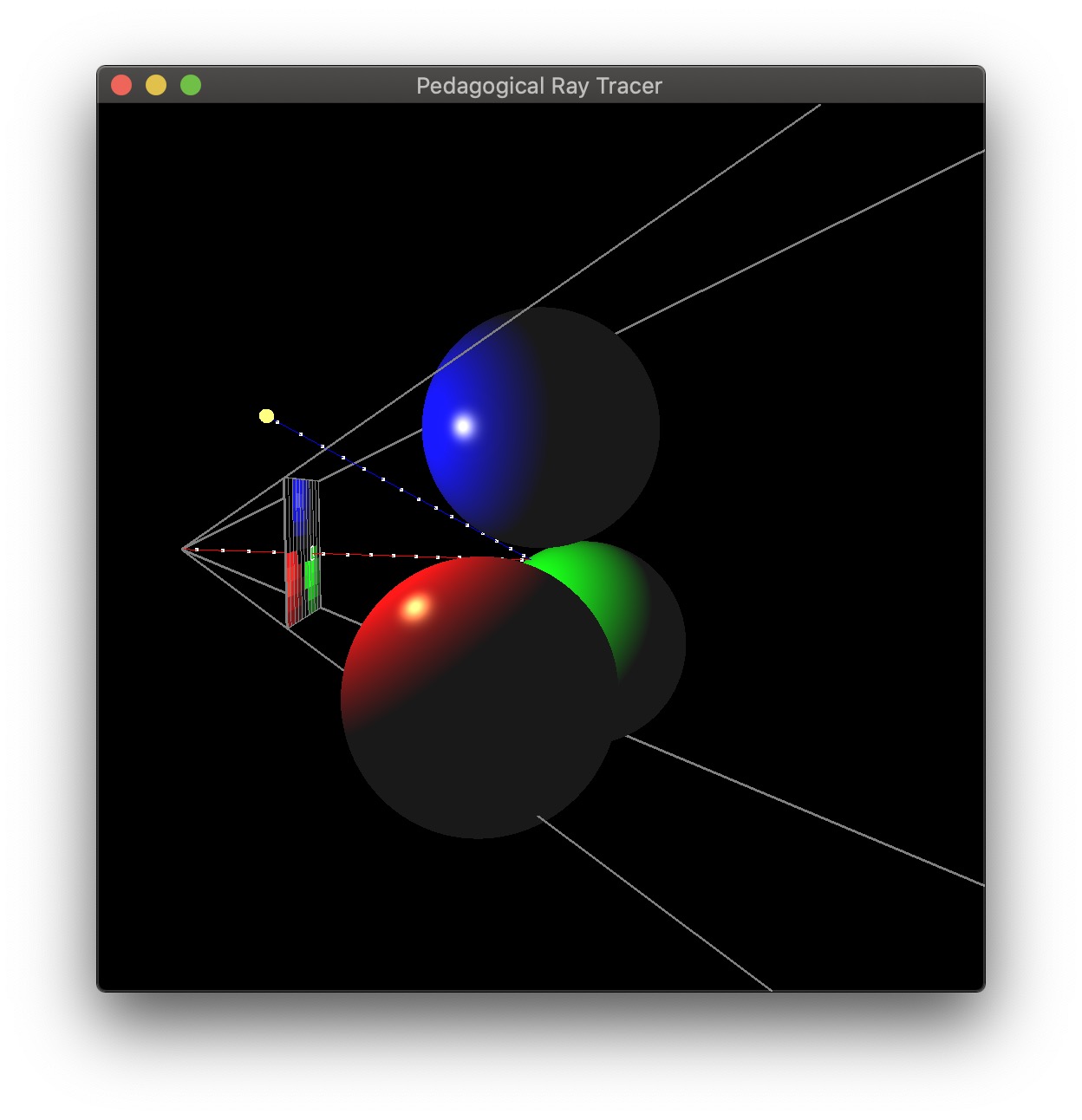
Your second scene will consist of one sphere, one ellipsoid, one infinite plane, and two lights.

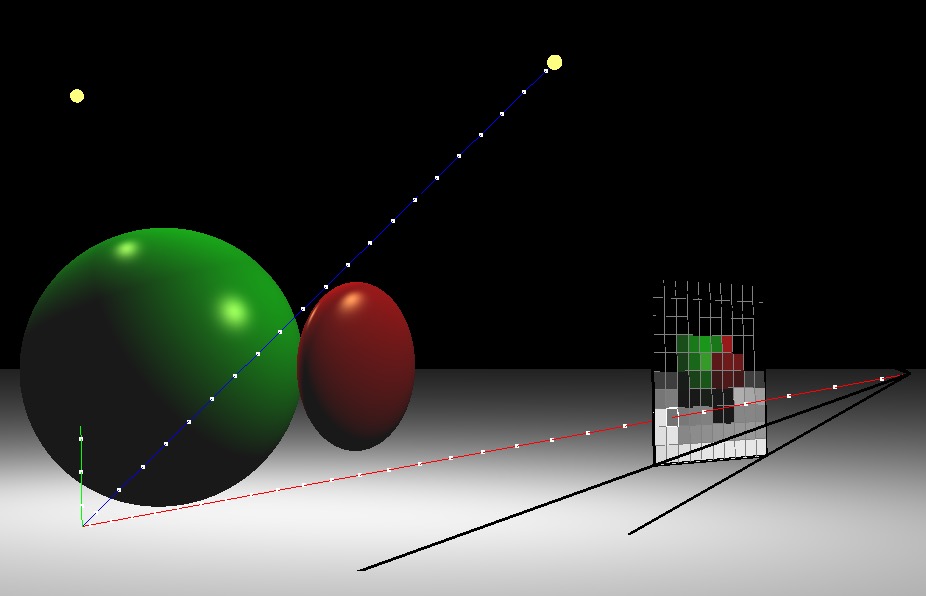
(Left) Ray traced scene. (Right) A rotated view showing one of the view rays. The blue shadow ray reaches the light, but the green shadow ray is blocked.
Light 1
(1.0, 2.0, 2.0)0.5Light 2
(-1.0, 2.0, -1.0)0.5Red Ellipsoid
(0.5, 0.0, 0.5)(0.5, 0.6, 0.2)(1.0, 0.0, 0.0)(1.0, 1.0, 0.5)(0.1, 0.1, 0.1)100.0Green Sphere
(-0.5, 0.0, -0.5)(1.0, 1.0, 1.0)(0.0, 1.0, 0.0)(1.0, 1.0, 0.5)(0.1, 0.1, 0.1)100.0Plane
(0.0, -1.0, 0.0)(1.0, 1.0, 1.0)(0.0, 0.0, 0.0)(0.1, 0.1, 0.1)0.0With two lights, you should be able to see areas that are occluded from both or just one light. Also note that the ellipsoid casts a shadow on the sphere.
Your third scene consists of two lights, two Phong spheres, two reflective spheres, and two infinite planes.
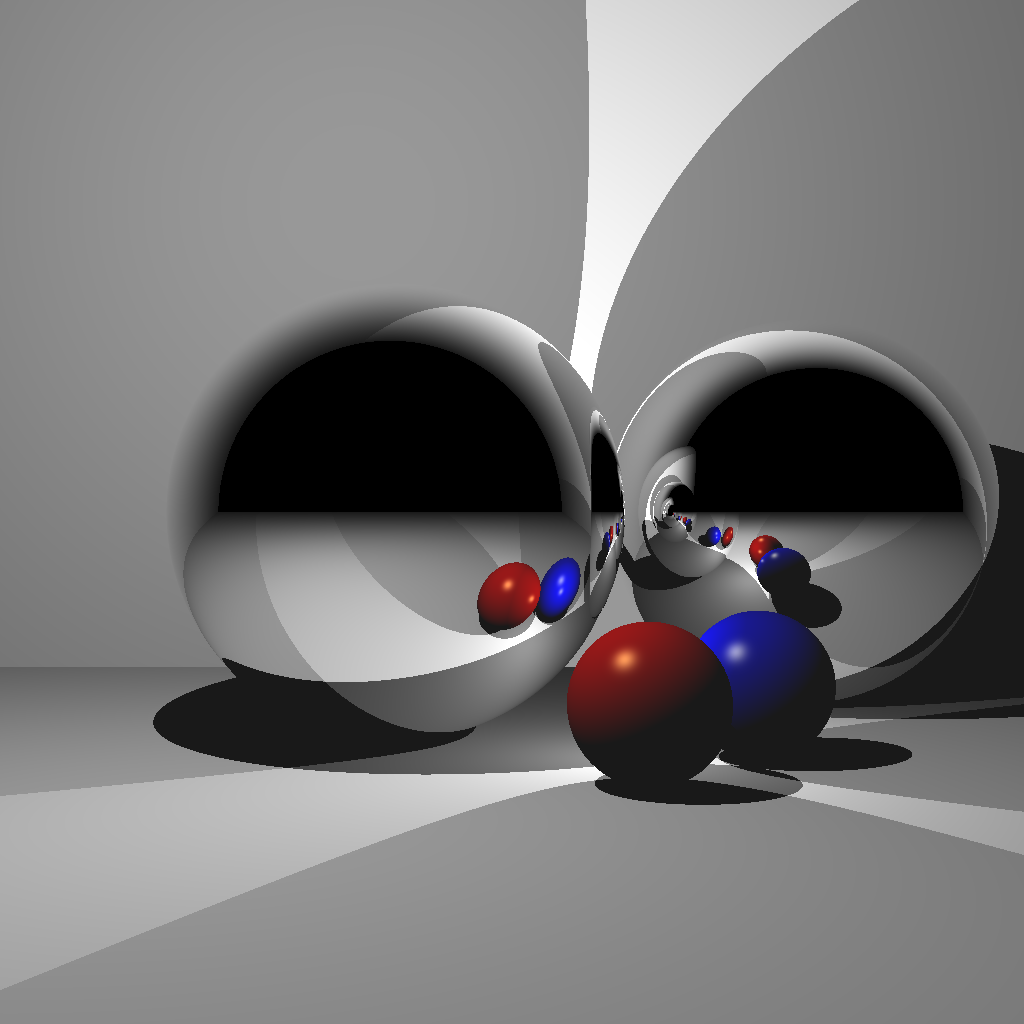
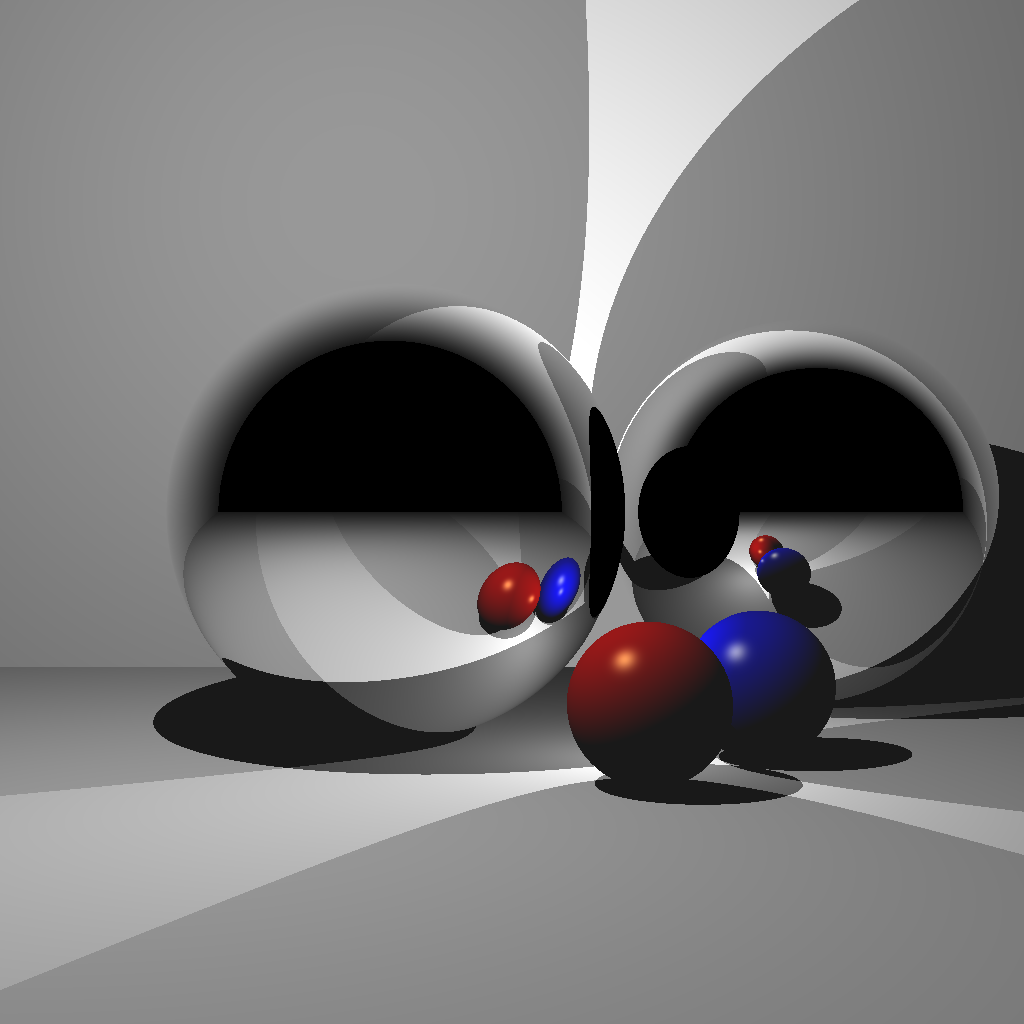
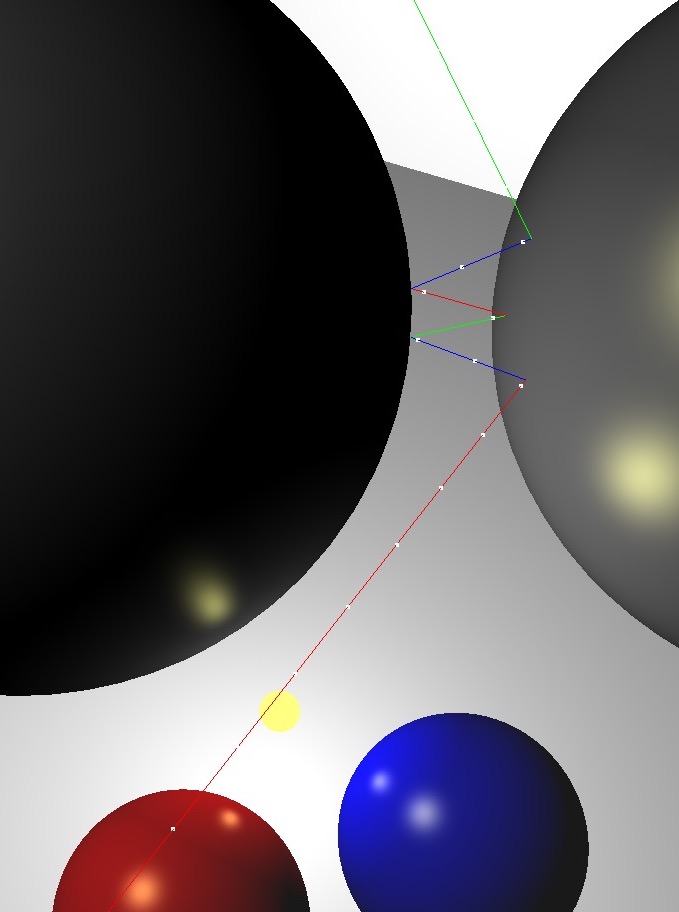
(Left) Ray traced scene. (Center) Without enough recursion depth, the reflection of the other reflective sphere is not rendered. (Right) A closeup of multiple reflections.
First, you should get a single reflection to work (center image). Then, you should implement multiple reflections to get rid of the black regions in the spheres.
Light 1
(-1.0, 2.0, 1.0)0.5Light 2
(0.5, -0.5, 0.0)0.5Red Sphere
(0.5, -0.7, 0.5)(0.3, 0.3, 0.3)(1.0, 0.0, 0.0)(1.0, 1.0, 0.5)(0.1, 0.1, 0.1)100.0Blue Sphere
(1.0, -0.7, 0.0)(0.3, 0.3, 0.3)(0.0, 0.0, 1.0)(1.0, 1.0, 0.5)(0.1, 0.1, 0.1)100.0Floor
(0.0, -1.0, 0.0)(1.0, 1.0, 1.0)(0.0, 0.0, 0.0)(0.1, 0.1, 0.1)0.0Back Wall
(0.0, 0.0, -3.0)(1.0, 1.0, 1.0)(0.0, 0.0, 0.0)(0.1, 0.1, 0.1)0.0Reflective Sphere 1
(-0.5, 0.0, -0.5)(1.0, 1.0, 1.0)Reflective Sphere 2
(1.5, 0.0, -1.5)(1.0, 1.0, 1.0)Import an obj mesh. For triangle-ray tests, use the optimized code by Thomas Akenine-Moller. Some hints:
1 or 0 depending on whether there was a hit.orig and dir are the ray origin and direction, respectively.vert0, vert1, and vert2 are the three vertex positions of the triangle.t is the distance along the ray where the hit occurred.
t > 0 to deal with collisions happening behind the ray.u and v are the barycentric coordinates of the triangle where the hit occurred.
u corresponds to vert1, and v corresponds to vert2.Without any optimizations, using the bunny mesh will take a very long time to render, since each ray will need to be tested against every single triangle. Add a simple optimization by putting a bounding sphere around the bunny and testing the ray against the sphere first. If the ray does not hit the sphere, you do not need to test against any of the triangles. It should take less than a minute to render a bunny with a single light at 512x512 resolution.


Finally, add the ability to transform the obj mesh. To do this, you need to transform the ray into local coordinates, perform collision detection, and then transform the result back to world coordinates. Let \(E\) be the 4x4 transformation matrix of the obj mesh. Then:


Implement a camera that can be translated/rotated arbitrarily in the world and whose field of view can be modified. For grading purposes, use the same setup as Scene 1. In other words, Scene 5 should be the same as Scene 1 but from a different camera location/orientation. In the images below, the camera is at (-3,0,0) looking along the positive X axis, with the field of view of 60 degrees. The left image is the 3D view from the original view point of Scene 1, and the right image is the resulting ray traced image. To receive credit, you need to be able to reproduce this ray traced image.

Set up your program so that when the <SCENE> argument is set to 0, the program generates an interesting image using what you have implemented (Spheres, ellipsoids, mesh, etc.). You may want to attempt the two bonuses below before completing Scene 0. The most interesting images will be given bonus points (details TBA).
Find code online to accelerate the ray-triangle intersection for Scene 4. You can use a sphere-tree, OBB-tree, oct-tree, KD-tree, BSP-tree, etc. Remember to cite the source in the code and in the README.
Implement refraction and generate an interesting image. Use 6 for the <SCENE> argument.

Total: 100 plus 20 bonus points.
Failing to follow these points may decrease your final score.
On Linux/Mac, make sure that your code compiles and runs by typing:
> mkdir build
> cd build
> cmake ..
> make
> ./A5 <SCENE> <IMAGE WIDTH> <IMAGE HEIGHT> <IMAGE FILENAME>If you’re on Windows, make sure that you can build your code using the same procedure as in Lab 0.
(*.~), or object files (*.o). You should hand in the minimum set of files you need to compile plus the README file.USERNAME.zip (e.g., sueda.zip). The zip file should extract everything into a folder named USERNAME/ (e.g. sueda/).
src/, resources/, CMakeLists.txt, and your README file to the current directory..zip format (not .gz, .7z, .rar, etc.).