Home

Assignment 1 - Rasterizer

Due Wednesday 1/29 at 11:59 pm. You must work individually.

Goal

Create a program that reads in and renders a triangle mesh (of type .obj) to an image via software rasterization. You may use existing resources to load in the mesh and to write out an image. You must write your own rasterizer. In general the required steps for the program are:

• Read in triangles.
• Compute colors per vertex.
• Convert triangles to image coordinates.
• Rasterize each triangle using barycentric coordinates for linear interpolations and in-triangle test.
• Write interpolated color values per pixel using a z-buffer test to resolve depth.

Associated Labs

• Lab -1 (required): Setting Up Your Development Environment. For A1, only the compiler and CMake are required, so only Lab Negative One is required, not Lab Zero.
• Lab 1 (optional): Bounding Box Rasterizer. See this lab if you need an example of how the Image class is used.
• Lab 2 (optional): Single Triangle Rasterizer.

Setting Up Your Code

Download the Assignment 1 base code, which has a mesh loader and an image writer. Compile and run the code by following the same set of commands as in Lab 0.

The mesh loader is an obj loader from http://github.com/syoyo/tinyobjloader, and the image writer is from http://github.com/nothings/stb.

When the mesh is loaded, the vertex positions are stored in the posBuf array as follows:

-----------------------------------------------------------------------------------------------
| x0 | y0 | z0 | x1 | y1 | z1 | x2 | y2 | z2 | x3 | y3 | z3 | x4 | y4 | z4 | x5 | y5 | z5 | ... <- posBuf array
-----------------------------------------------------------------------------------------------

|   vertex 0   |   vertex 1   |   vertex 2   |   vertex 3   |   vertex 4   |   vertex 5   |
|                 triangle 1                 |                 triangle 2                 |

Every three consecutive vertices in this array forms a triangle. In other words, every nine elements form the (x,y,z) coordinates of the three vertices of a triangle. Example mesh files are included in the base code. In addition, there are numerous OBJ meshes on the web. For grading purposes, your program will be run using the provided Stanford Bunny and Utah Teapot.

Ultimately you will want each triangle to be represented in a C/C++ structure/class, with 3 vertices and a color per vertex. In addition, your triangle data should include a 2D bounding box, which will represent the triangle’s extents in image coordinates.

Add a command line argument to accept the following command line arguments.

1. Input filename of the .obj file to rasterize
2. Output image filename
3. Image width
4. Image height
5. Coloring mode (0, 1, or 2)

For example, your program should be able to be run as follows:

> ./A1 ../resources/bunny.obj output.png 512 512 1

In Xcode, the 1st argument should be ../../resources/bunny.obj. Add error checking to specify the required command line arguments if an incorrect number are given. Your program should not dump core if no input file is specified, or fail without an error message! Follow the golden rule; treat your user/grader/instructor the way you’d like to be treated as a user/grader/instructor.

Drawing Bounding Boxes

Write code to convert each 3D coordinates into 2D image coordinates. Assume the camera is at the origin looking down the negative z axis. Make sure the object completely fills the image without any distortion. To do so, you need to compute the scale and translation factors as we discussed in class. Some tips for starting out:

• You’ll need a bounding box for the whole mesh as well as for each triangle.
• Color each triangle with a different random color.
• Start with tri.obj, which contains a single triangle.

First, write out the bounding box, rather than the triangles, to the image. If you do this with the provided tri.obj, sphere.obj, teapot.obj, and bunny.obj, you should see blocky images like below. Make sure the object takes up the whole image, is centered, and is undistorted (not stretched).

Drawing Triangles

Once the bounding boxes are being displayed correctly, add the barycentric test to write out the triangles as in (optional) Lab 2. You should not see any gaps between the triangles.

Make sure you test nonuniform window sizes. As shown below, the aspect ratio of the object should be preserved no matter what the image size is, and the object should fill out the image.

Here is another image of a bunny and a teapot, from Alice in Wonderland [Wikimedia].

Interpolating Per-Vertex Colors

Instead of using random per-triangle colors, use random per-vertex colors. For each pixel inside each triangle, you need to interpolate the pixel’s color from the three vertices using the pixel’s barycentric coordinates. This should be the output when the “coloring mode” command line argument is set to 0.

Optional information: Because of the way we are loading the mesh, the triangles do not share any vertices. For example, if we were to load a square consisting of four vertices and two triangles, we end up with six vertices – three for each of the triangles. In other words, we end up duplicating any shared vertices. Therefore, when we assign a color to each vertex, triangles having a vertex at a common position can have different colors assigned at this vertex position. For example, in the sphere image above, the center vertex is incident to eight triangles, and so it has been duplicated eight times, each time with a different random color. For further information check out indexed drawing.

Z-Buffer

Now that you have interpolated colors, implement z-buffer tests. First, create a data structure to support z-buffer tests. Your z-buffer should be a separate buffer from your image pixel buffer, and it should be the same size as your pixel buffer. The z-buffer contains the z-coordinate of each pixel, which is interpolated from the z-coordinates of the three vertices using the pixel’s barycentric coordinates. Once you have z-buffer implemented, you should be able to render tri2.obj properly – the two triangles should be intersecting.

Now, use the z value of the pixel as the color. (You can choose any color, not just red.) To do this, you have to map the z-value to the range 0 to 255. If your z-buffer test is not working, you’ll see some strange results, since some pixels that are farther from the camera may be drawn on top of closer pixels. Use “color mode” 1 for this task.

Additional Color Mode

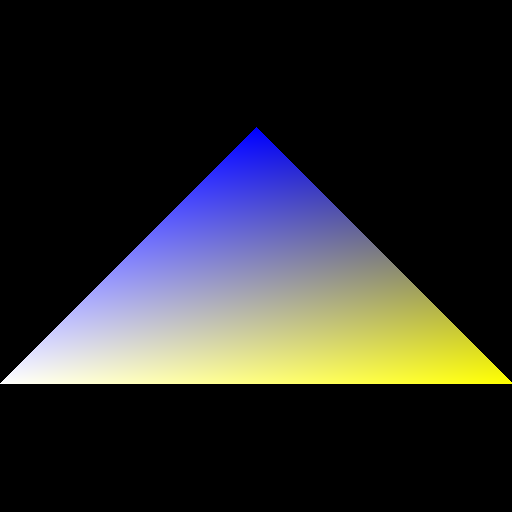
Add an additional “color mode” 2, where you use the y-value to linearly interpolate two colors of your choice. For example, in the right figure below, I am interpolating between yellow and cyan. Make sure to specify these two colors in your README. The color should vary smoothly from top to bottom.

Important Note

Make sure to pass your std::vector by reference rather than by value. (E.g., void foo(std::vector<float> &bar)) Otherwise, your program may become too slow. Since the Image class has an std::vector inside it, it should also be passed by reference.

Point breakdown

• 10 points for image coordinate transforms for square images.
• 5 points for image coordinate transforms for non-square images.
• 20 points for correct rasterization of triangles.
• 15 points for color mode 0: per-vertex colors.
• 20 points for correct z-buffer implementation.
• 10 points for color mode 1: depth colors.
• 10 points for color mode 2: y colors.
• 10 points for coding style and general execution. For example, do not put everything in main(), and do remember to pass big data by reference.

Total: 100 points

What to hand in

Failing to follow these points may decrease your “general execution” score. Make sure that your code compiles and runs by typing, for example:

> mkdir build
> cd build
> cmake ..
> make
> ./A1 <ARGUMENTS>

• Make sure the arguments are exactly as specified.
• Include an README file (ascii or PDF) that includes:
  • Your name
  • The two colors for the last coloring mode
  • Citations for any downloaded code (e.g., barycentric)
  • Plus anything else of note
• Remove unnecessary debug printouts.
• Remove unnecessary debug code that has been commented out.
• Hand in src/, CMakeLists.txt, and your README file.
• Do not hand in the build directory, the executable, input obj files, output image files, old save files (*.~), or object files (*.o).
• Create a single zip file of all the required files. The filename of this zip file should be USERNAME.zip (e.g., sueda.zip). The zip file should extract everything into a folder named USERNAME/ (e.g. sueda/).