Due Wednesday 3/25 Friday 3/27 at 11:59 pm. You must work individually.
Create a 3D world you can walk through. Implement freelook for camera motion.
There is no base code provided for this assignment. Please start with your previous lab/assignment code. Please come see me or the TA if you need help completing your previous assignment.
Write some code so that you can add multiple objects to the world. Each object should have a transformation matrix so that you can easily translate/rotate/scale/shear the object in the world. (Note that in order to transform the normals properly, you’ll need to send the inverse transpose matrix as a parameter to the shader if you include shear or non-uniform scales. If you only have uniform scales, you can multiply them by the plain old modelview matrix and normalize the result.) For this initial stage, since we’re using the primitive camera from previous assignments/labs, the objects that you add to the world may have to be small so that they’re visible from the camera. Once you implement freelook, you can re-transform these objects to distribute them in the world the way you want.

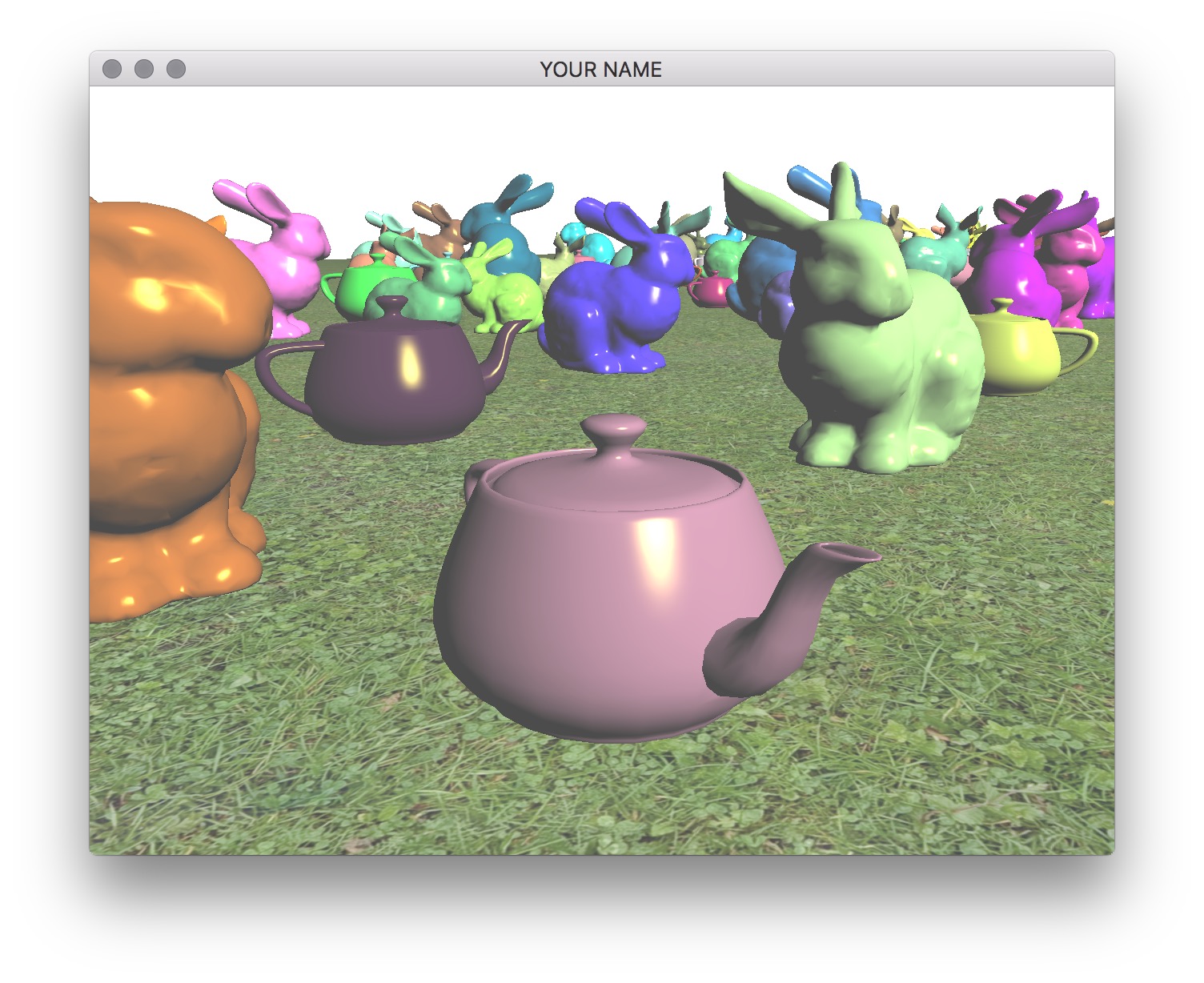
You should include at least two types of shapes. For example, here I’m using the bunny and the teapot. You can use any model, but please try to keep the file sizes reasonable. If you download a model, please put a citation in your readme. Note that some OBJ files may not come with normals or texture coordinates. You should add at least 20 things in the scene. In addition to these two types of shapes, add a ground plane.
It is important to load each OBJ file just once, even if you are going to draw that shape multiple times. I suggest you make another class that represents an object in the world. This class should have a pointer/reference to a shape instance.
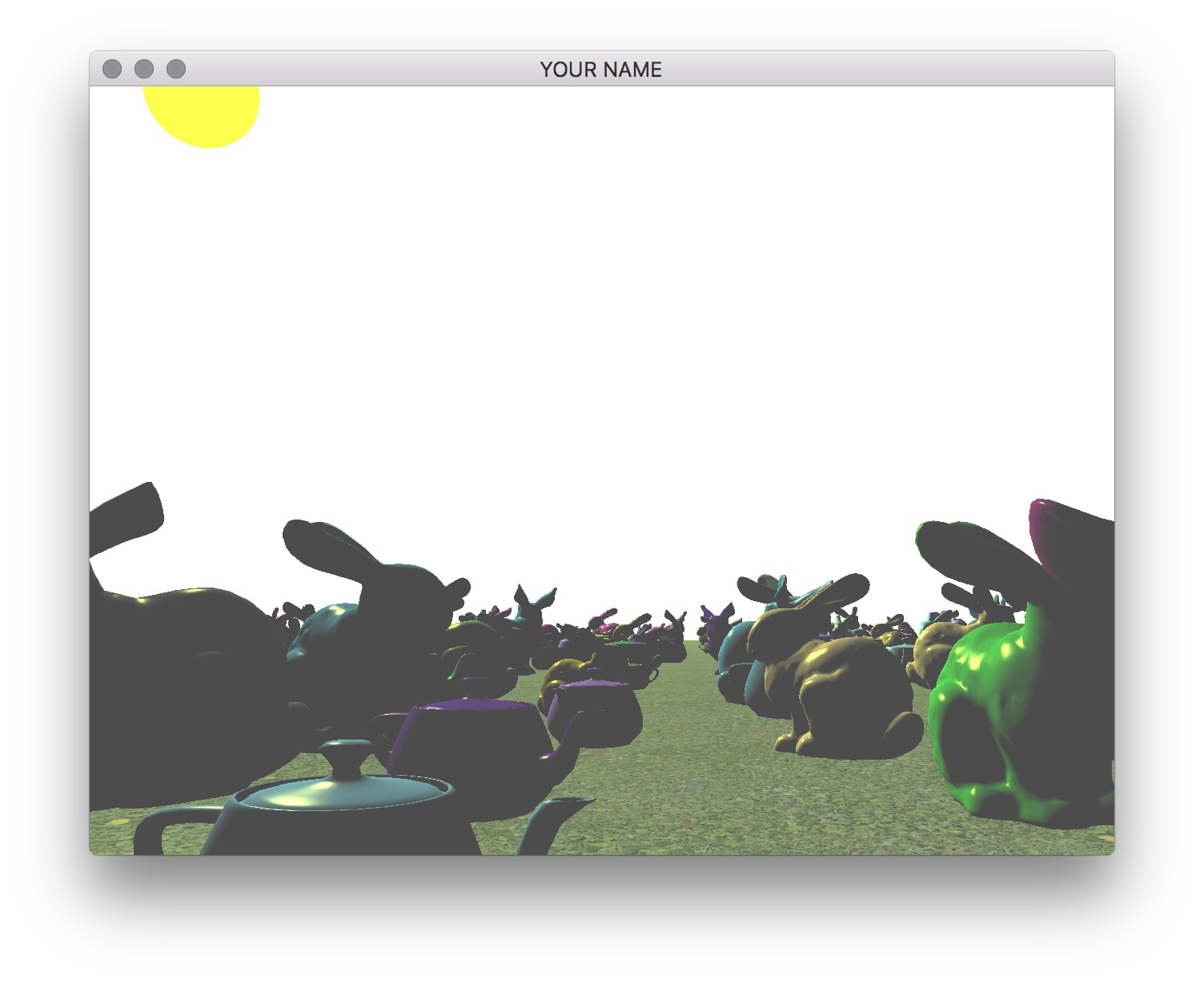
Use your Blinn-Phong shader from your previous assignment to shade the models. For bonus points, you can use a texture for the material parameters, as in Lab 9. Unlike the last assignment, the light position should be fixed in the world. This means that the light position is no longer a constant in camera space. You need to choose a world space position for the light and then multiply this position by the view matrix (modelview matrix before adding any modeling transforms) to transform the light position into camera space.
Finally, draw a sphere where the light is. The lighting on the objects in the scene should match this location of the light source. Note how, in the image below, the left side of the green bunny is correctly lit by the light in the upper left corner of the image.
Now replace the Camera class with your own class that implements freelook. You can reuse the applyProjectionMatrix() method, but you’ll need a new applyViewMatrix() method. To implement freelook, the new camera class needs to keep track of its position, yaw, and pitch. From these three quantities, you need to come up with the correct arguments for the glm::lookAt() function.
The general setup of your code should be as follows:
render() method in main.cpp, the first matrix in the modelview matrix stack should be filled by the applyViewMatrix() method of your new freelook camera class. In the applyViewMatrix() method, you should use the glm::lookAt() method to create this view matrix.The eye, target, and up arguments of the lookAt() function are:
eye: camera positiontarget: camera position + “forward” directionup: the Y vector, \((0, 1, 0)^T\), (assuming Y-up)Position
I suggest fixing yaw and pitch first so that you can get basic translation correct with no rotation. The initial position of the camera should incorporate the height of the camera off of the ground.
Add keyboard hooks for WASD for translation:
Pressing these keys should update the translation of the camera.
For now, the “forward” direction can be set to the negative Z direction, which is the default camera direction in OpenGL. When the ‘w’ key is pressed, the camera should move along this “forward” direction. In the applyViewMatrix() method of your camera class, feed this new translation value into the lookAt() function.
Yaw
Now add yaw to your freelook camera, which allows you to look right and left. The X-motion of the mouse should be tied to the yaw angle of the camera. Look at the previous camera class from the labs to see how mouse inputs are handled.
The “forward” direction should be computed based on the yaw angle. If the ground is on the y=0 plane, then the forward direction is
\[ \vec{f} = \begin{pmatrix} \sin(\theta)\\ 0\\ \cos(\theta) \end{pmatrix}, \]
where \(\theta\) is the yaw angle. The ‘w’ key should now move the camera along this new “forward” direction, rather than the negative Z direction. The “left” direction (or the “right” direction) can be computed using the cross product. If this is working properly, pressing the ‘w’ key should make your camera move in the direction that it is facing.
Pitch
Finally, add the pitch angle, which allows you to look up and down. The Y-motion of the mouse should be tied to the pitch angle of the camera. Unlike the yaw angle, the pitch angle should be capped at some reasonable limits (e.g., -60 to +60 degrees). The pitch angle should change the “target” argument of the lookAt() method, since it changes the “forward” direction that the camera is looking at. However, it should not change the direction of motion. In other words, even if the camera is looking up or down, pressing ‘w’ should not change the height of the camera. (The camera should not lift off of or go into the ground.)
Transform the objects over time using the glfwGetTime() function. (See the image below.)
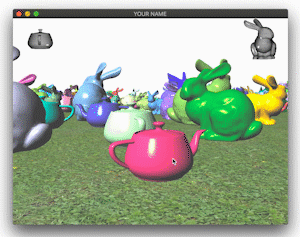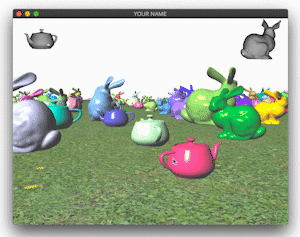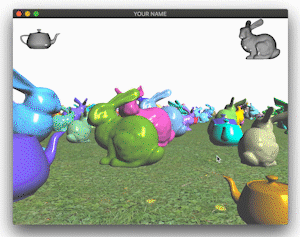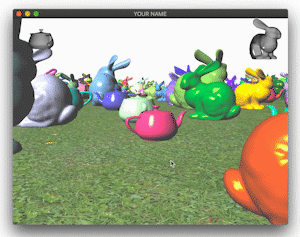
Total: 105 points
Failing to follow these points may decrease your “general execution” score. If you’re running Linux/Mac, make sure that your code compiles and runs by typing:
> unzip USERNAME.zip
> cd USERNAME
> mkdir build
> cd build
> cmake ..
> make
> ./A4 ../resourcesIf you’re running Windows, make sure that you can build your code using the same procedure as in Lab 0.
For this assignment, there should be only one argument. You can hard code all your input files (e.g., obj files) in the resource directory.
src/, resources/, CMakeLists.txt, and your readme file. The resources folder should contain all required input obj and texture files.(*.~), or object files (*.o).USERNAME.zip (e.g., sueda.zip). The zip file should extract everything into a folder named USERNAME/ (e.g. sueda/).
src/, resources/, CMakeLists.txt, and your README file to the current directory..zip format (not .gz, .7z, .rar, etc.).