Using collections
This section is devoted to collections -- how to create them,
resize them, change the way they look, and navigate into them.
Collections are really new spaces. Once you have created a
collection, you can think of it as a porthole into this space. You
can put objects into collections, and enter the collections to work
with the objects inside. The instructions below will tell you
how.
Selecting.
Selecting a collection is just like selecting an object. Just click on the collection's border. Knots will appear to show you that the collection is selected.
Moving.
Collections can be moved when they are selected. Just drag them around using the left mouse button.
Changing color.
You can change the color of a collection by using the buttons across the top of the window. It will change the background color of the whole space. You can also change the line width of its border.
Creating.
To create a new collection, use the button on the top of the VIKI window:

Press the button down. It will look like this:

Now click down in the space. You will see a new (empty) collection:
Giving a collection a name.
If you click in the area immediately above the collection, you will see a blinking straight up-and-down cursor. This will allow you to type in a name for the collection.
Back to Introduction
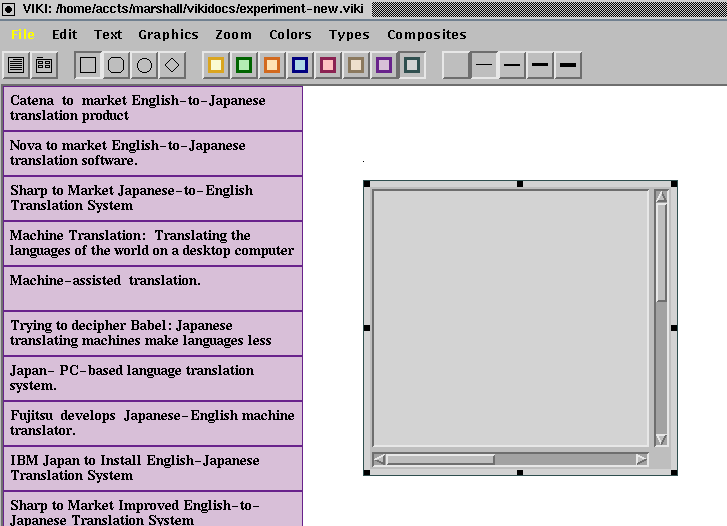
Putting an object in a collection.
You can move an object into a collection by dragging it on top of the collection. The edges of the collection will act as a clipping region if you move the object toward the edge of the collection:
Reshaping.
Collections can be reshaped. Just select the collection, and drag one of the knots. You can reshape them to any size:

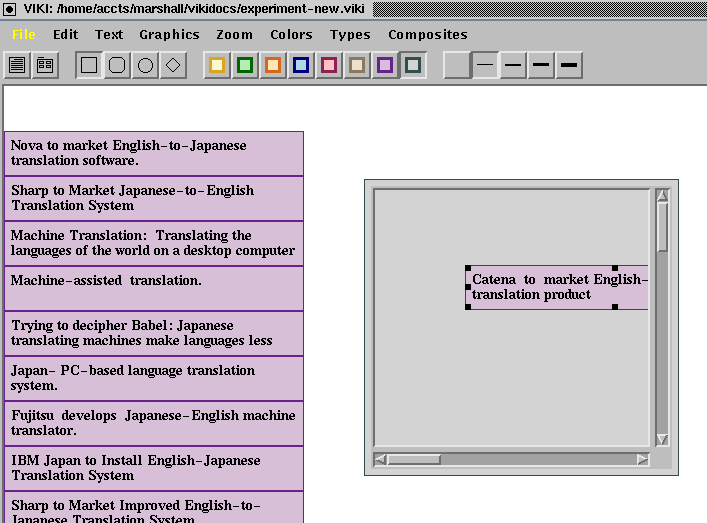
Navigating into a collection.
Once you've moved objects into a collection, you may want to "enter" the collection to work with the objects. All you have to do is double-click on the border of the collection. It should resize itself to occupy the entire window:
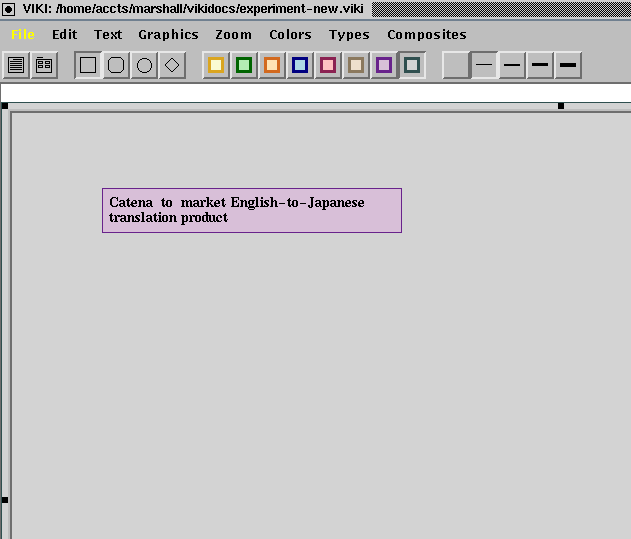
When you're through working in a collection, double-click on its border, and it will shrink back to its former size. You will be back in the original space.
Return to Introduction





