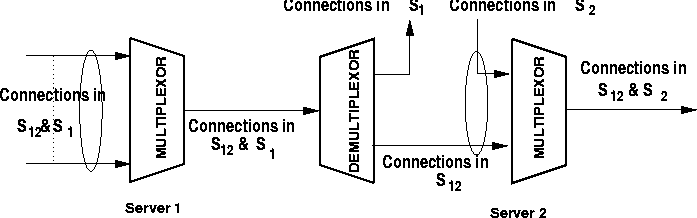
In this section, we study a subsystem with two multiplexors, the topology for this subsystem is illustrated in Figure 1. An integrated method for the delay analysis in this system is presented. Although the approach is generic in nature, we will assume that the multiplexors are use a FIFO scheduling policy.
Figure 1: A Subsystem with two Multiplexors.
To evaluate the worst-case delay suffered by traffic, the description for network traffic is needed. We give the following definitions and notations for this purpose.
Similarly, we define the amount of traffic leaving the server as follows:
Referring to the two-server subsystem depicted in
Figure 1, we use 
to denote the set of
all connections that traverse both Server 1 and Server 2. We use
to denote the set of all connections that traverse
Server 1 only and then leave the subsystem. We use 
to
denote the set of all connections that join the subsystem after
Server 1 and traverse Server 2 only.
Throughout this paper, we will assume that the traffic of every
connection is controlled at the source by a token bucket, that is, for
or 
The delay at a server can be determined once the output traffic at that server is known. The following lemma, which was first presented in [1], addresses this.
Once we know the output traffic of a server, we also know the arrival time for the data leaving at any particular point in time. The following lemma gives the relationship between the output traffic and the data arrival time.
The lemma follows from the definition of function 
.
Q.E.D
Similarly, we can formulate when the arriving data will leave the server, as the following lemma shows.
The lemma follows from the definition of function 
.
Q.E.D
We can now apply these results to accurately determine the end-to-end delay suffered by traffic as it traversed the two-server subsystem depicted in Figure 1.
During the time interval [0,t), the total amount of traffic arriving
at Server 2 is 
. According to Lemma 3, the
-th bit leaves Server 2 at time 
.
Furthermore, these contains 
bits coming from
Server 1. According to Lemma 2, the -th bit
arrives at Server 1 at time 
. Therefore, the delay
suffered at time t by connections traversing both servers is given
as 
. So we have
Q.E.D
Unfortunately, Equation (8) is only of theoretical value.
This is because it requires the knowledge of internal network traffic
(in form of ). Since the only information we assume are the
traffic constraint functions at the sources, and the traffic is not
reshaped internally, the internal network traffic is difficult, if not
impossible, to describe. In order to provide a useful integrated
method for delay analysis in this subsystem, we need to deeply analyze
Equation (8).
The following central theorem in this paper provides an estimation for
in Lemma 4
To streamline the presentation of the theorem, we define the following
auxiliary notations:
.
.
.
.
.
See Appendix. Q.E.D
We note that, according to Theorem 1, the end-to-end
delay 
of connections traversing both servers can be
computed using only bounding functions for the traffic entering the
subsystem. This eliminates the problems described earlier with
Equation (8) and provides a practical method to analyze
end-to-end delays, as we proceed to describe below.
