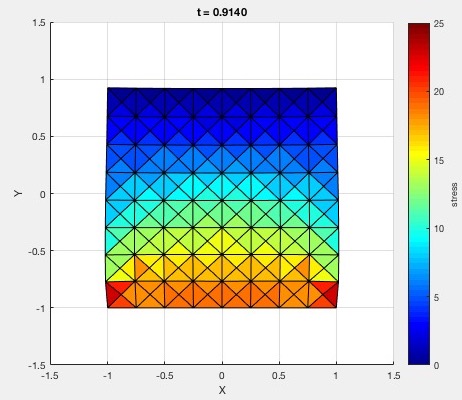
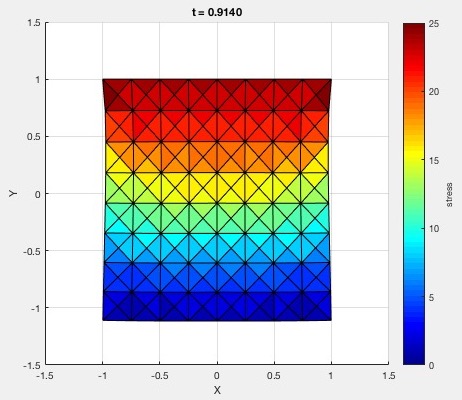
Left: bottom nodes are fixed. Right: top nodes are fixed.
Due Wednesday 11/8 at 11:59 pm. You must work individually.
In this assignment you will implement the finite element method for triangular meshes in MATLAB. We will provide skeleton code and you will be responsible for filling in critical, excised sections.
In particular, you will implement:


Left: bottom nodes are fixed. Right: top nodes are fixed.
Download the base Matlab code. The provided code is standalone and does not require any external libraries. Copy or move fem2D.m to WORKINGDIR. Then open Matlab, go to the command window, and type:
>> cd <WORKINGDIR>
>> fem2DMatlab will then open a figure window that shows a simple scene with four triangles. The nTiles variable in case 0 controls the number of triangles in the discretization. Note that the physical size of the object does not change. As you work on the code, you should verify that changing nTiles does not radically affect the behavior of the object.
There are two main arrays of structures in the code: nodes and tris.
nodes: Each element of this array represents a node (aka particle or vertex), and it has the following fields:
X: The original (reference) positionx: The current (world) positionv: The current (world) velocitym: Mass, distributed from the neighboring triangles, which you have to implement. This is initially zero.f: Sum of forces. This will have to be reset to zero every step.fixed: A boolean indicating whether this node is pinned to the world or free to move around.tris:
nodes: This is a 3x1 array that contains the indices of the three nodes of this triangle. The nodes are ordered counter-clockwise.stress: Once you compute the stress, you should store it here so that the color can be based on this value.You may add more fields as you see fit.
The first task is to write code to compute the Lamé parameters (\lambda and \mu) from Young's modulus (E) and Poisson's ratio (\nu). Look at the notes for the formulae. Poisson's ratio of around 0.3-0.4 will produce reasonable results. You should not use 0.5 (volume preserving), as this will cause a division by zero. Young's modulus should be around 1e2.
Next, compute the mass of the nodes by computing the triangle area and distributing the mass to the nodes. The mass of the triangle should be \rho A, where \rho is the area density, and A is the area of the triangle defined by Xa, Xb, and Xc. Make sure to cite whatever reference you use for the triangle area. When nTiles=1 and rho=1e0, the masses of the 5 nodes should be 0.6667 for the four corner nodes and 1.3333 for the center node.
Inside the simulation loop, add velocity and position integrations. Following the notes, use the implicit damping formulation for the velocity step and the simple explicit formulation for the position step. Make sure to skip over nodes that are fixed by checking the fixed field of the node. Once this step is done, try running the simulation. If damping=0.0, you should see the object stretching very fast, since we still have not implemented the elastic (FEM) force. If damping is set to a high value, you should see the object stretch slowly.
This is the main part of the assignment. In the simulation loop, add a loop over the triangles and compute:
All the required equations are in the notes. To access the nodes of the kth triangle, use the nodes field of the triangle as follows:
triNodes = tris(k).nodes;
xa = nodes(triNodes(1)).x;
xb = nodes(triNodes(2)).x;
xc = nodes(triNodes(3)).x;You may also need the X field (reference positions) of the nodes in order to compute the deformation gradient, though it is better to precompute the inverse of the X matrix outside of the simulation loop.
To compute the nodal forces, you'll need to iterate through the three edges of each triangle. In 2D, to compute the vector that is orthogonal to another vector, you can simply flip the x- and y- coordinates and negate one. For example, for an arbitrary 2D vector \vec{a},
will generate a 2D vector \vec{b} that is orthogonal to \vec{a}. This can be derived from the cross product.
h should be pretty small, around 1e-3. If your simulation is exploding, reduce it further.Once you have the simulation code working, create different types of scenes by changing the parameters. For each of these, take a screenshot and list the parameters. If a simulation explodes, note why (e.g., dt was too big) and write about it in the README. Please use the following numbering for the scene argument. Use StVK for Scenes 2 and 3, and Neo-Hookean for all other scenes.
1x1, 2x2, 4x4, and 8x8 with just the bottom nodes fixed. All four of these simulations must share the same parameters. They should behave in a similar manner.
8x8 with just the top nodes fixed. Tweak the parameters so that the bottom nodes roughly reach y=-1.5 and stay there after some oscillation.
Repeat the simulation above with two different values of Poisson's ratio. Describe the difference in the behavior. (Note: \nu cannot be 0.5.).
With 8x8, pin just the left nodes. You'll have to tweak the parameters again to make this work. If there is too much stress on a triangle, the simulation will likely blow up.
With 8x8:
axis(...) and caxis(...) in the draw(...) function). If you comment out these two lines, the axes will be adjusted automatically so that you can see what the limits are.EXTRA CREDIT (for both 489/689): Create a 2D simulation mesh either from scratch or using an OBJ loader. Make sure to cite any references. Be careful about the size of the mesh. Our simple FEM code will not be able to handle large meshes. (We'll need implicit integration if we want to take larger time steps.)
Make sure to set up your code so that all your different scenes (1-6 above) can be run simply by changing the argument to the main function (e.g., fem2D(5)). For different subscenes within a scene (e.g., Scene 1 with different resolutions), you can simply hardcode the parameters and rerun the code.
Please follow these instructions carefully. If you fail to follow these instructions, you will be docked some points.
Please provide a report with your submission (PDF). The report should include the following:
Create a zip file named NETID.zip (your email ID; e.g., sueda.zip) so that when you extract it, it creates a folder called NETID/ (e.g., sueda/) that has (ONLY) the following in it:
fem2D.m)