Due Wednesday 10/18 at 11:59 pm. You must work individually.
In this assignment, you are going to implement and analyze the following optimization algorithms:
Start with the base Matlab code. Run the code by typing the following at the Matlab prompt:
>> driver(0)
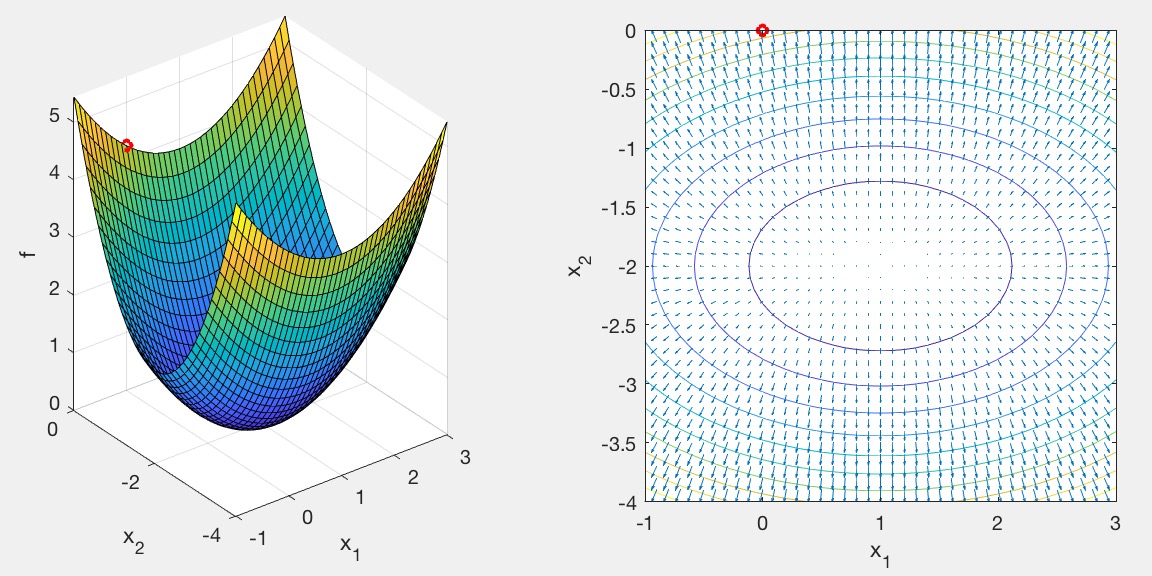
The left subplot is a 3D function, f(x,y), that you're trying to find the minimum of. The right subplot is the corresponding contour/quiver plot. The starting point of the search is shown as a red circle.
Currently, two test functions are implemented in fun.m. To switch between different test scenarios, change the driver argument. driver(1) and driver(2) use the same prob, but have different starting points---one is far from the optimum solution and the other one is closer.
Implement the gradient descent algorithm:
The test functions in fun.m return the function value f and gradient g, given an input point x. It also computes the Hessian matrix H, which will be used later for Newton's Method. In your driver, pfun(x) has been mapped to evaluate the function without entering fnum, and so these two are equivalent and can be used interchangeably:
[f,g,H] = pfun(x);
[f,g,H] = fun(x,fnum);To check for convergence, test whether the norm of the current step vector (\|\Delta \vec{x}\|) is smaller than thresh.
Inside the iteration loop, plot the value of x in red in both the left and right subplots. This can be done by copying and pasting the code from lines above the loop:
subplot(1,2,1);
plot3(x(1),x(2),f,'ro:','LineWidth',2,'MarkerSize',5);
subplot(1,2,2);
plot(x(1),x(2),'ro:','LineWidth',2,'MarkerSize',5);With the current value of \alpha, the convergence is really slow because the iterates keep on overshooting to the other side of the valley. Do some "hyper parameter optimization." In other words, tweak \alpha so that the algorithm converges faster.
Try the other test case by running driver(1).
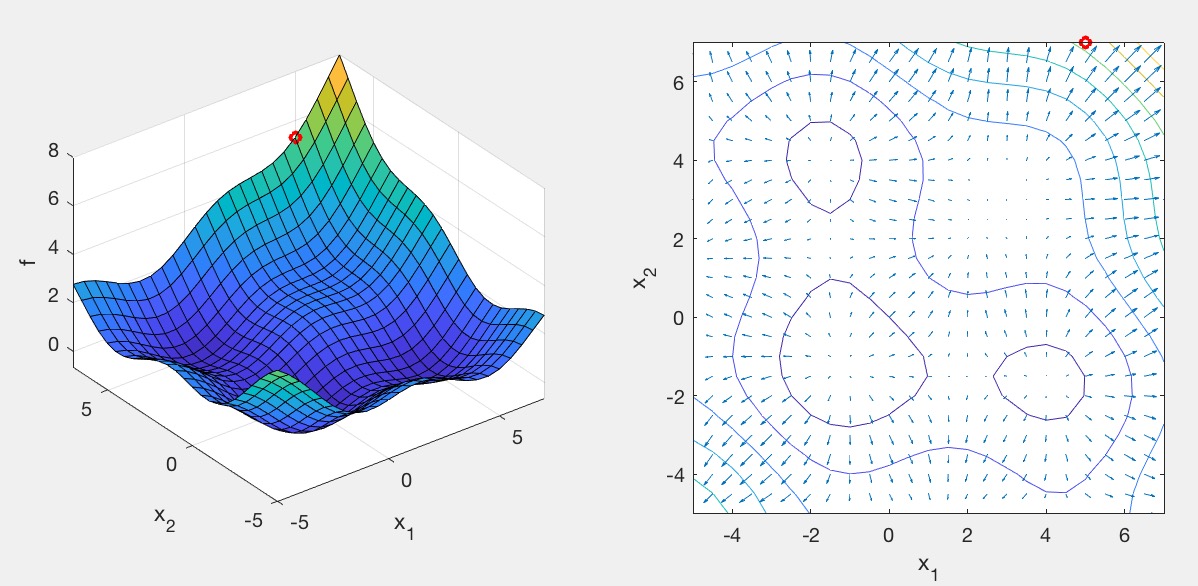
This test case has multiple local minima as well as a saddle. If you run your current Gradient Descent code, you will find that it converges to a saddle. We can improve the algorithm by adding momentum:
Like before, plot the value of x inside the iteration loop, this time in green. Once the algorithm is implemented, tweak \beta so that the algorithm converges faster.
Try running driver(2). This is the same function as driver(1), but zoomed in near the solution. Even though we are starting the search very close to the solution, Gradient Descent, even with momentum, is quite slow to converge. Newton's Method addresses this:
Like before, plot the value of x inside the iteration loop, this time in blue. Notice how quickly it converges, given that we are close to the solution.
Please provide a report with your submission (PDF). The report should include the following.
driver(0):
driver(1):
driver(2):
driver(3) and driver(4) with a new custom function in fun.m.
fnum = 2).
driver(3) should start the search far from the solution.driver(4) should start the search close to the solution.Create a zip file named NETID.zip (your email ID; e.g., sueda.zip) so that when you extract it, it creates a folder called NETID/ (e.g., sueda/) that has (ONLY) the following in it: