Home

Lab 6 - Forward Kinematics / Hierarchical Modeling

Today we’re going to create a simple hierarchical robot.

Please download the code for the lab and go over the code. When you run the code, you should see a background grid. When you press the space bar and move the mouse, you should see some console output. These values correspond to the location of the mouse on the screen, with each grid line representing one unit. These mouse coordinates are not needed for this lab but will be used in the inverse kinematics assignment.

This lab uses Eigen for linear algebra. You’ll have to install Eigen in the same way you installed GLM in L00. You’ll need to create a new environment variable called EIGEN3_INCLUDE_DIR that points to the Eigen directory. Once you have it installed, you may want to look at this quick tutorial.

Take a look at the Link class. It has the following member variables:

• A pointer to the parent link.
• A pointer to the child link. For this lab and the assignment, we will assume that we have a serial chain of links without any branching.
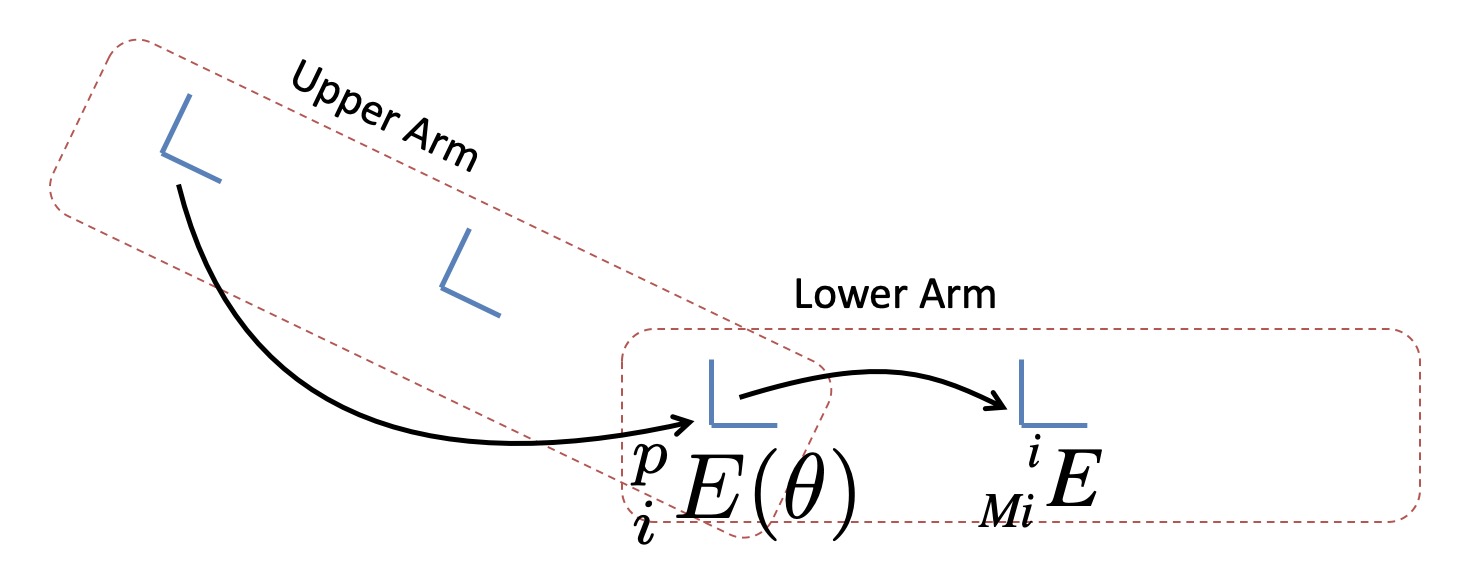
• An int for the “depth” of the link, with the root having index $0$.
• A Vector2d representing the XY position $\overrightarrow{p}$ of the link joint wrt the parent joint.
• A double for the current angle, $\theta$.
• A Matrix4d, ${}_{Mi}^{i}E$, for the transform of the mesh with respect to this link joint.

Since you’re going to create a 2D planar mechanism, you only need a single scalar for the rotation. For convenience, the origin of each link is going to be where the joint is. For example, for the “upper arm” link, the origin will be at the shoulder, and for the “lower arm” link the origin is going to be at the elbow. Using the position $\overrightarrow{p}$ and the rotation $\theta$ member variables, the transformation matrix from the parent link’s joint to this link’s joint is:

$${}_i^{p}E(\theta )=T(\overrightarrow{p})R(\theta ).$$

The leading superscript $p$ is for “parent” (not “position”), and the leading subscript $i$ is for the ith body. The product above should give you a 4x4 matrix that looks like this:

$${}_i^{p}E(\theta )=\left(\begin{array}{cccc}\cos (\theta )& -\sin (\theta )& 0& {\overrightarrow{p}}_x\\ \sin (\theta )& \cos (\theta )& 0& {\overrightarrow{p}}_y\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right).$$

In other words, using the left-to-right interpretation, we translate the coordinate system with $\overrightarrow{p}$, and then we rotate the coordinate system with $\theta$.

The arrows indicate what the two transformation matrices represent. ${}_i^{p}E$ describes where the current link is with respect to the parent link. In the figure above, it represents where the elbow joint is with respect to the shoulder joint. ${}_{Mi}^{i}E$ describes where the mesh’s origin is with respect to the current link.

The pseudocode for the recursive drawing function is as follows. Note that you will have to pass in the MV matrix stack into this function so that you can send the modified matrix to the GPU.

void Link::draw(MatrixStack &M) {
    M.push();
    M.mult(jointMat); // where this joint is wrt parent
    M.push();
    M.mult(meshMat); // where the mesh is wrt this joint
    Send M's top matrix to the GPU
    drawMesh();
    M.pop();
    child.draw(M);
    M.pop();
}

Note that the MatrixStack class has been augmented to take an Eigen matrices as well as glm matrices.

There are three TODOs in the skeleton code.

• Link::draw(...)
• init() in main.cpp
• render() in main.cpp

Implement these TODOs so that you can see the links moving by pressing the . and , keys: