In this lab, we’re going to use bilinear interpolation to deform a 2D mesh.
Please download the lab and go over the code.
When you compile and run the source code, you should see a 2D figure with a cage around it. The cage is draggable, but it won’t do anything until you implement a couple of functions. You can change the grid size by modifying grid->setSize() in the init() function in main.cpp.
Set the grid size back to (2, 2) to get a 2 by 2 array of grid points. Take a look at the function ShapeCage::load(). The posBuf vector is being filled with the data from the obj file. In the ShapeCage::toLocal() function, which is called once at the beginning of the program, this data is being passed through without modification to the posLocalBuf vector, and in the ShapeCage::toWorld() function, which is called every frame, this data is being passed back to the posBuf vector. (Note that posBuf is of size 3*nVerts, since it comes from the input obj file, whereas posLocalBuf is of size 2*nVerts, since only the 2D local coordinates are stored.) This obviously does nothing when the grid moves. What you want to do instead is to properly compute the local coordinates and then compute the world coordinates from the local coordinates PLUS the new grid configuration.
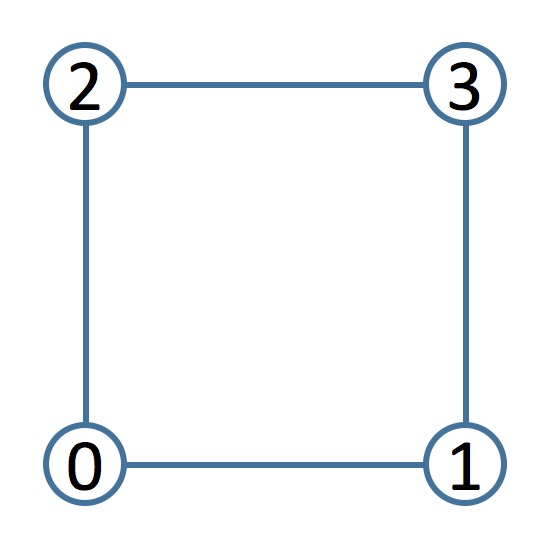
First, implement the ShapeCage::toLocal() function. For now, since there is only one tile in the grid, you can ignore the tileIndexBuf vector. (We will be using this later when we increase the grid size.) For each vertex, posLocalBuf should store where that vertex is with respect to the grid tile — i.e., its local coordinates. To get the four control points of the 0th tile (currently our one-and-only tile), use the following:
vector<glm::vec2> cps = grid->getTileCPs(0);The returned vector cps contains the four control points in this order:

To compute the local coordinates (u, v) of a vertex, get the minimum and maximum (x, y) world coordinates of the tile, and then use the following formula:
\[ u = \frac{x - x_\min}{x_\max - x_\min}, \qquad v = \frac{y - y_\min}{y_\max - y_\min}. \]
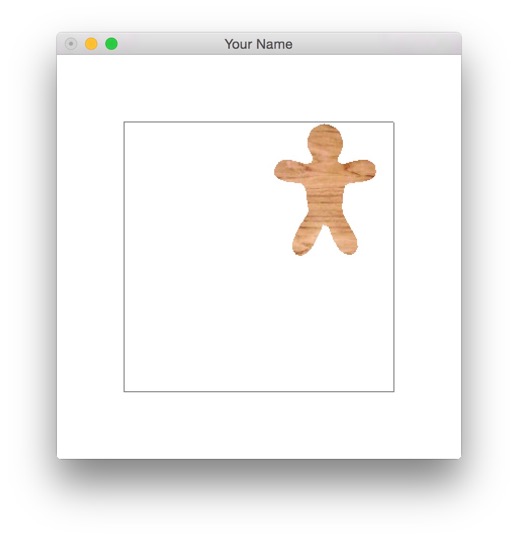
Once the local coordinates are computed properly, you should see the character in the top right corner as shown. This is because the world goes from (-1, -1) to (1, 1), and the local coordinates are between 0 and 1. Once we implement toWorld() in the next task, the character will fill the whole tile again.
Now implement ShapeCage::toWorld(). In this function, you should do the reverse of the transformation you applied above so that the posBuf vector is filled with proper values. In other words, for each vertex, apply the bilinear interpolation function:
\[ \begin{aligned} & P_0(u) = (1 - u) P_{00} + u P_{01},\\ & P_1(u) = (1 - u) P_{10} + u P_{11},\\ & P(u,v) = (1 - v) P_0(u) + v P_1(u). \end{aligned} \]
You can get the four control points, \(P_{00}\) through \(P_{11}\) with the call to grid->getTileCPs(0) as before. You should now be able to move the character by moving the control points.

Increase the grid size to (5, 5). Since there are multiple tiles now, the current code does not work. You need to change both ShapeCage::toLocal() and ShapeCage::toWorld().
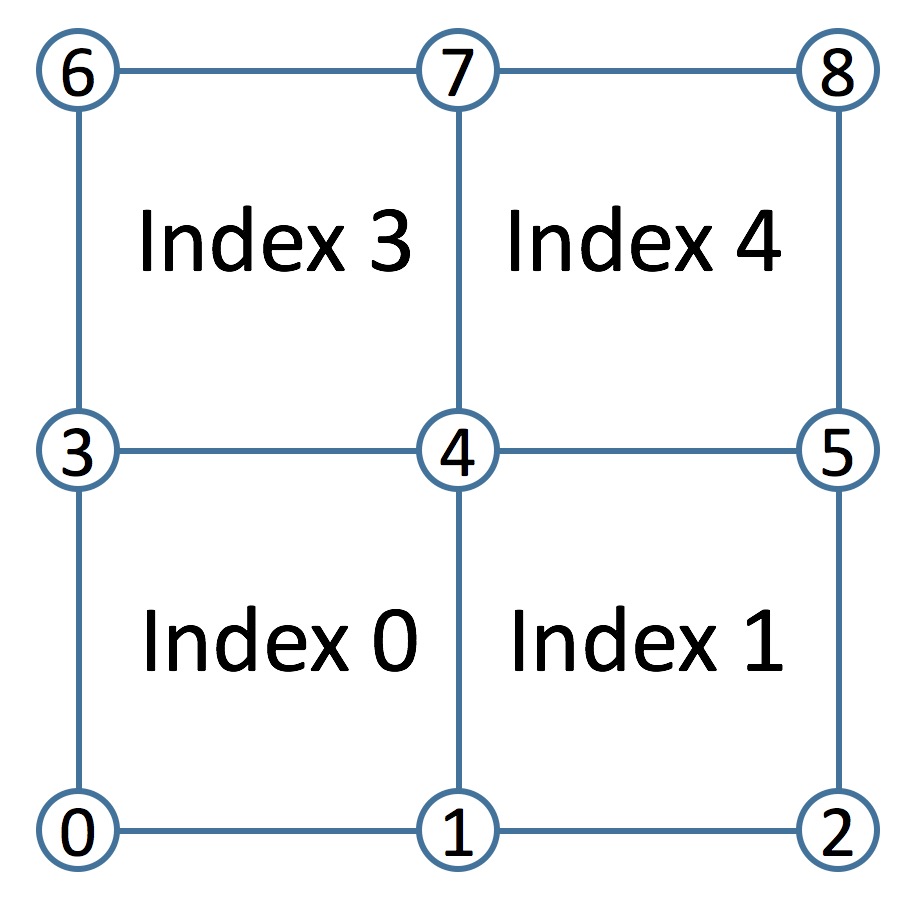
In ShapeCage::toLocal(), you need to find which tile each vertex belongs to by looping through all of the tiles. You can do this with a double for-loop using the nrows and ncols variables and a call to grid->indexAt(row, col).
// Find which tile this vertex belongs to
for(int col = 0; col < ncols-1; ++col) {
for(int row = 0; row < nrows-1; ++row) {
// Get the four control points for corresponding to (row, col)
int tileIndex = grid->indexAt(row, col);
vector<glm::vec2> cps = grid->getTileCPs(tileIndex);
//
// DO SOME STUFF HERE
//
}
}Keep in mind that nrows and ncols are the number of control points in the x and y directions, and so the number of tiles is nrows-1 by ncols-1. The tile index takes on the value of the control point at its lower left corner. For example, if nrows=3 and ncols=3, then the tile indices are:
In addition to the local coordinates, each vertex needs to store the tile index. Store this in the tileIndexBuf vector. Note that the length of this vector is nVerts, whereas the length of posLocalBuf is 2*nVerts.
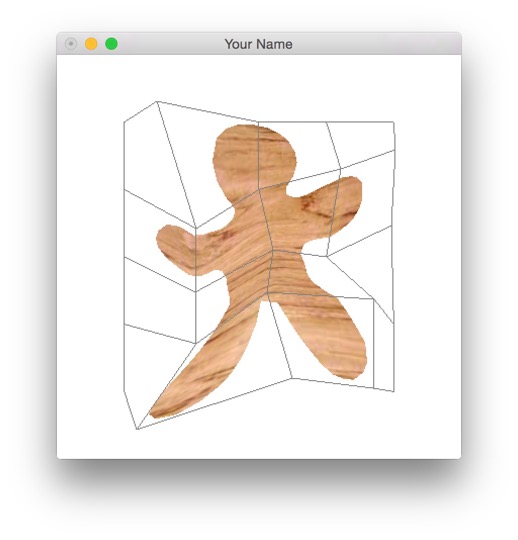
In ShapeCage::toWorld(), you should use both tileIndexBuf and posLocalBuf to compute the updated posBuf. First find the four control points you need from the tile index of the vertex. Then use bilinear interpolation to find the world coordinates of the vertex. You should now be able to move the numerous control points to pose the character.
Now we’re going to implement bilinear interpolation on the GPU. You should add a keyboard hook to switch between the CPU and the GPU versions.
The ShapeCage::toLocal() function is going to remain the same. However, you will no longer be needing the ShapeCage::toWorld() function, since you will be doing this transformation in the vertex shader. Think about what you need to do to replace this function with GPU code.
Miscellaneous tips:
Before, you were passing posBuf to the vertex shader as an attribute variable. Now you’ll be passing in posLocalBuf instead. You need to transform these positions from local to world in the vertex shader. Important: posBuf is loaded from the obj file, and so it contains (x,y,z) values for each position, but posBufLocal should only contain (u,v) values. Therefore, the 2nd argument to glVertexAttribPointer() should be 2, not 3.
In addition, you need to pass tileIndexBuf as an attribute variable. You’ll need to use a float rather than an int because some graphics cards do not support integer data types. In GLSL, you can cast a float to int using a C++ style cast.
float bar;
...
int foo = int(bar);You can hard code the grid size in the shader to (5, 5).
You can pass in the 25 control points as a uniform parameter. prog will have to be changed to match whatever variable name you’re using.
// In the vertex shader:
uniform vec2 cps[25];
...
// In main.cpp:
glUniform2fv(prog->getUniform("cps"), 25, glm::value_ptr(grid->getAllCPs()[0]));To access the four control points of the kth tile in the vertex shader:
vec2 cp00 = cps[k];
vec2 cp01 = cps[k + 1];
vec2 cp10 = cps[k + ncols];
vec2 cp11 = cps[k + ncols + 1];You’ll need to add a new argument to ShapeCage::draw() for the tile index attribute array.