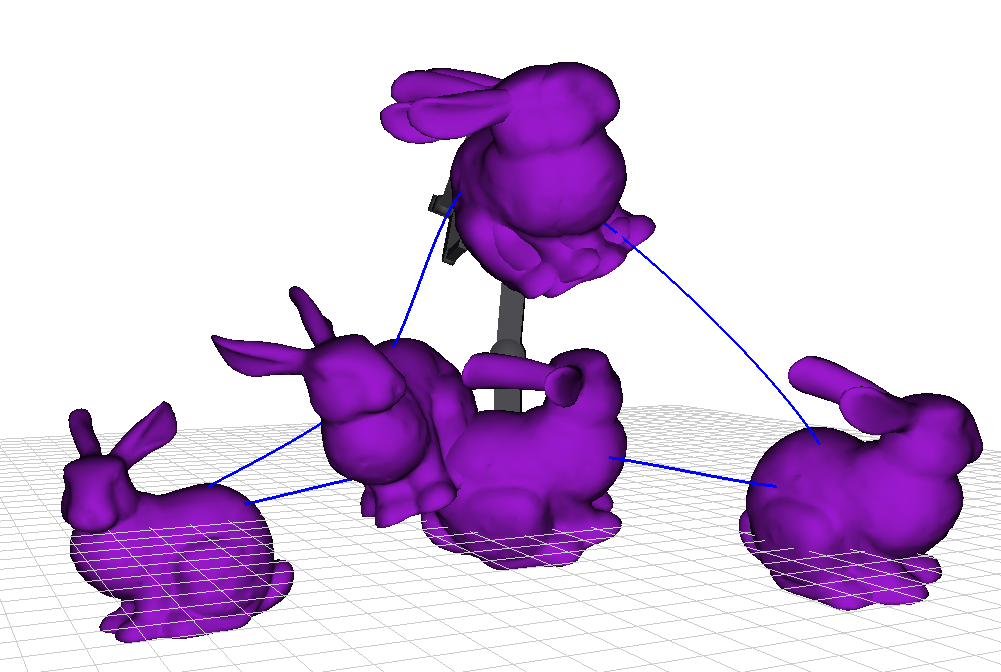
In my project, I decided to improve on Assignment 4, truning the code from 2 dimensions into 3 dimensions and adding multiple targets to be reached with an arm. The libraries used were the same as in Assignment 4, GLM, GLEW, GLFW, and Eigen.

The target is given by several control points on an object mesh. The user can specify a position and a rotation for the object mesh and all the end effectors will get close to the selected points. In the image below, the target points are in red and the end effectors are in green, but the bunny is too far away for the arm to reach it.

The arm consists of a chain on joints that eventually branches out into several independent subchains. For simplicity, each subchain is completely identical to the other subchains, but the angles on each arm are independent of the ones in the other arms. All the joints are revolute joints, which means that they have a single degree of freedom, and they rotate about the x, y, or z axis, depending on the specifications of the arm.
The biggest source of problems was the convergence of the algorithm. In multiple occasions, the arm got locked in a local minimum, forming something that resembles a knot, such as in the picture below.

The way I countered this was to improve my optimization algorithms. For Assignment 4, we implemented Gradient Descent with Backtracking Line Search, which would be followed by Newton's Method. I added momentum to the gradient descent computation, and Line Backtracking to Newton's Method. Adding momentum helped the algorithm to break free from points where the gradient is nearly zero, while adding Line Backtracking to Newton's method resulted in a remarkably faster convergence.
The basis of the momentum method is to store a weighted average of the gradients of previous iterations as the 'momentum'. Then, instead of using the direction of the gradient as the descent direction, we take a weighted sum of the momentum and the gradient as our descent direction. This way, if the gradient becomes too small, the momentum will give us a descent direction to break free from the local minima.
As a final touch, I used the code from Assignment 1 to keyframe a path for the object with rotations and translations. The arm will move across the path to follow the points along the path shown below. When the animation is active, it looks like the object is being moved by the arm, however the opposite is occurring inside the code: the target is placed according to the path information and the arm's angles adjust to the object.