Liam Bessell CSCE 489 Computer Animation Final Project



N-Body Problem

How do we simulate the movement of n-bodies when each body affects every other body?
Examples: Gravitational forces on stars, network visualization, molecular dynamics, and more.


Naive Simulation

Before attempting the Barnes-Hut simulation I first implemented the much easier Naive n-body simulation. I quickly discovered that the Naive simulation couldn't effectively run simulations with more than ~2000 bodies in real time. This is actually what kindled my interest in pursuing Barnes-Hut; I wanted to see massive galaxies move around in real time!

The Algorithm

    For each simulation step
  1. Loop through each body and calculate the force from every other body
  2. Update the positions and velocities


Barnes-Hut Simulation

This is an approximating simulation of the n-body problem.

The Algorithm

    For each simulation step
  1. Build the Octree
  2. Compute each node’s center of mass
  3. Approximate the force on each body by traversing the octree


Octrees

This data structure is the magic behind the Barnes-Hut simulation. It is essentially a normal tree with the caviat that every internal node has eight children. The octree is used for 3D Barnes-Hut because it is both fairly easy to implement and efficient. For 2D Barnes-Hut, a quadtree is used (Each internal node has four children).


Media




Octree Graphic

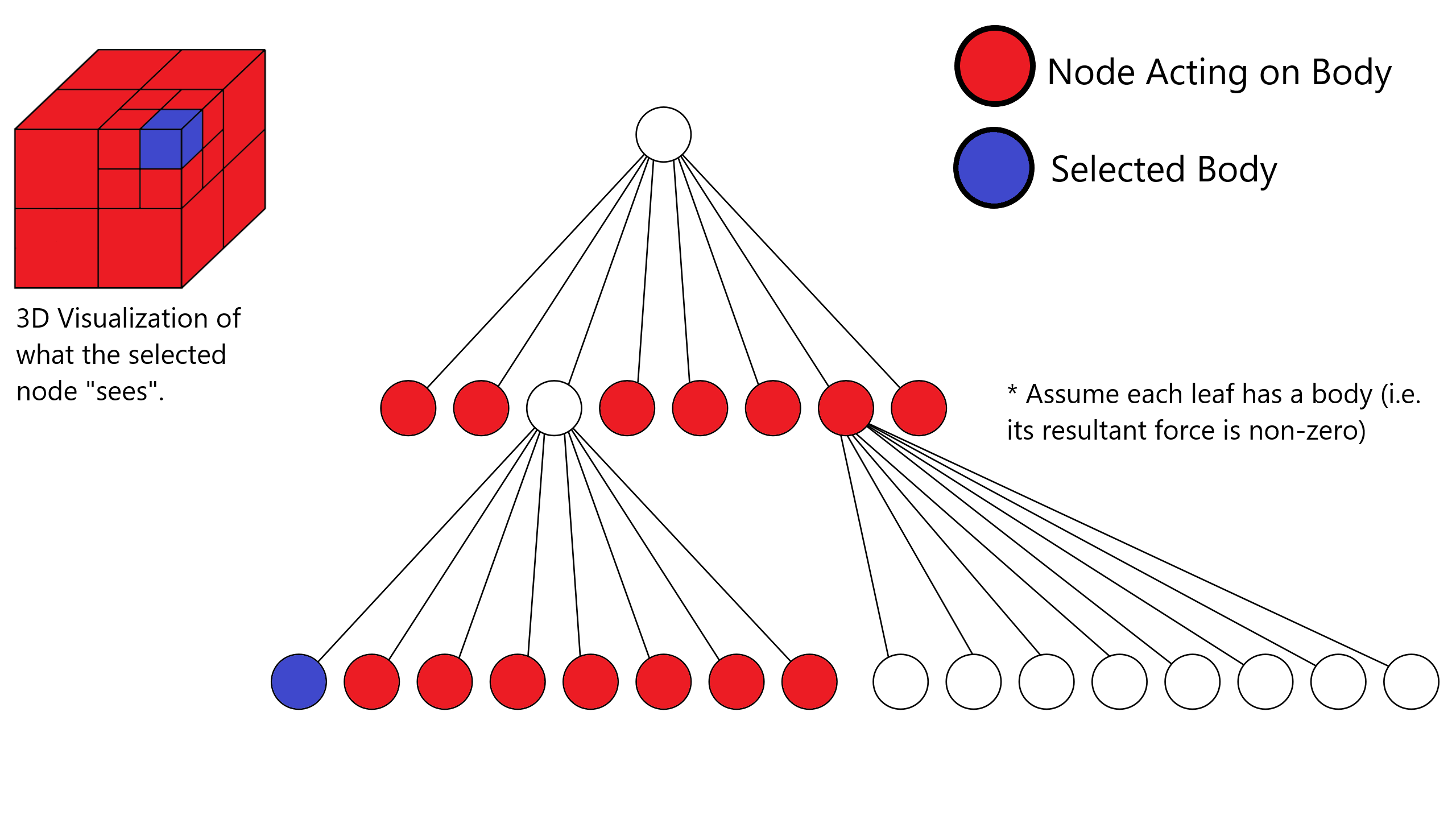
Octree Graphic


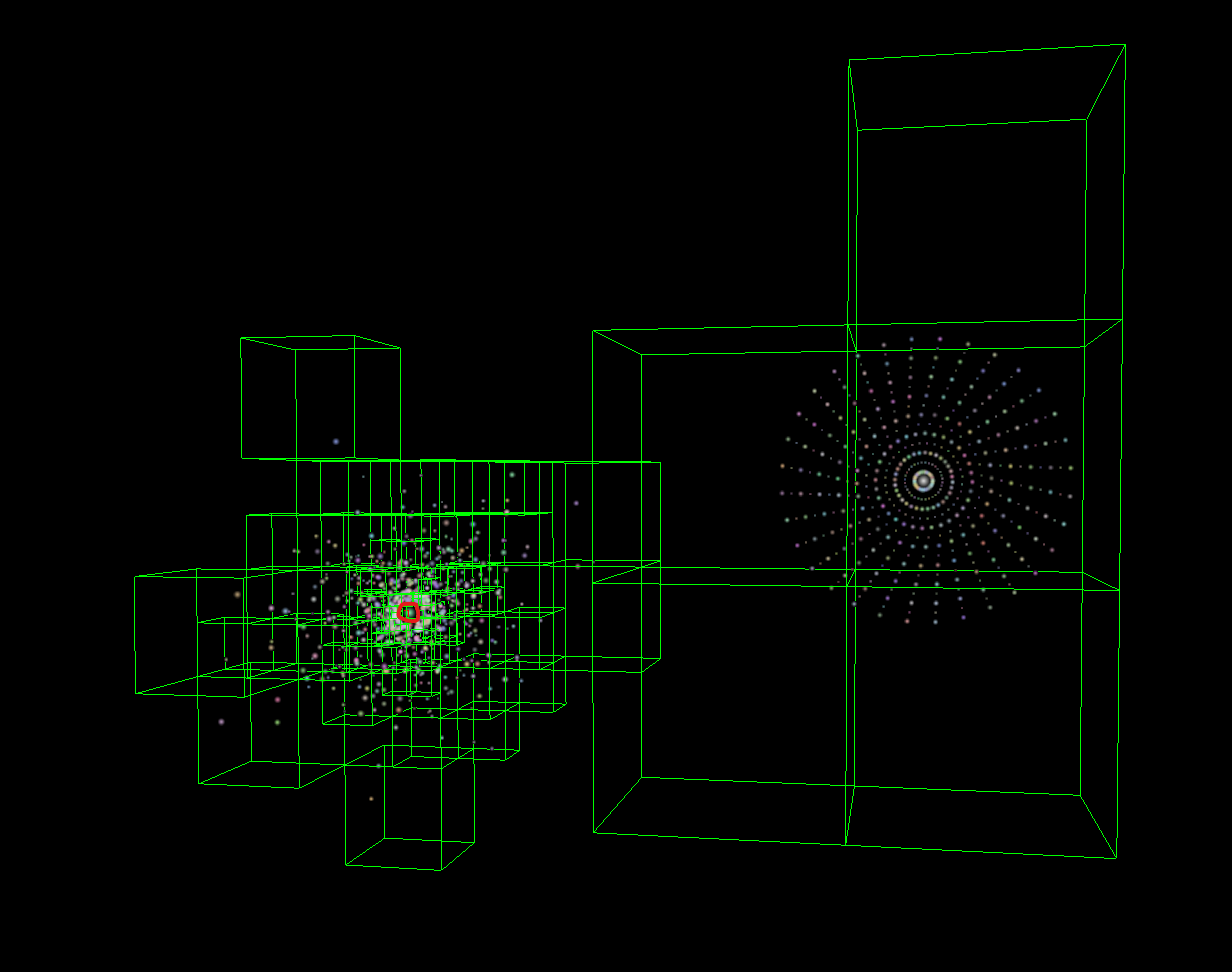
Octree Node Selected

This picture shows all the nodes that are acting on the selected body in the center of the left galaxy. Note that as bodies get farther away, their resultant force is more roughly approximated by using the larger node.

Octree Node Selected


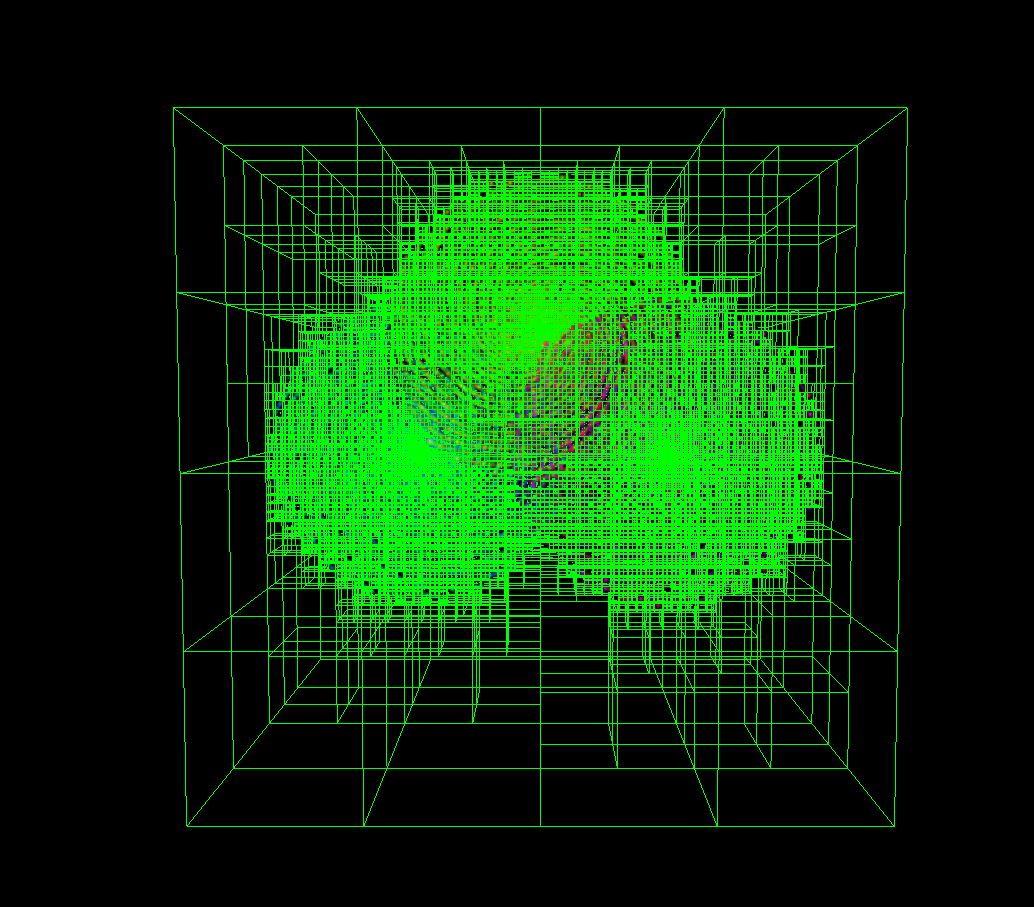
Octree with 10K Bodies

Octree 10K Bodies


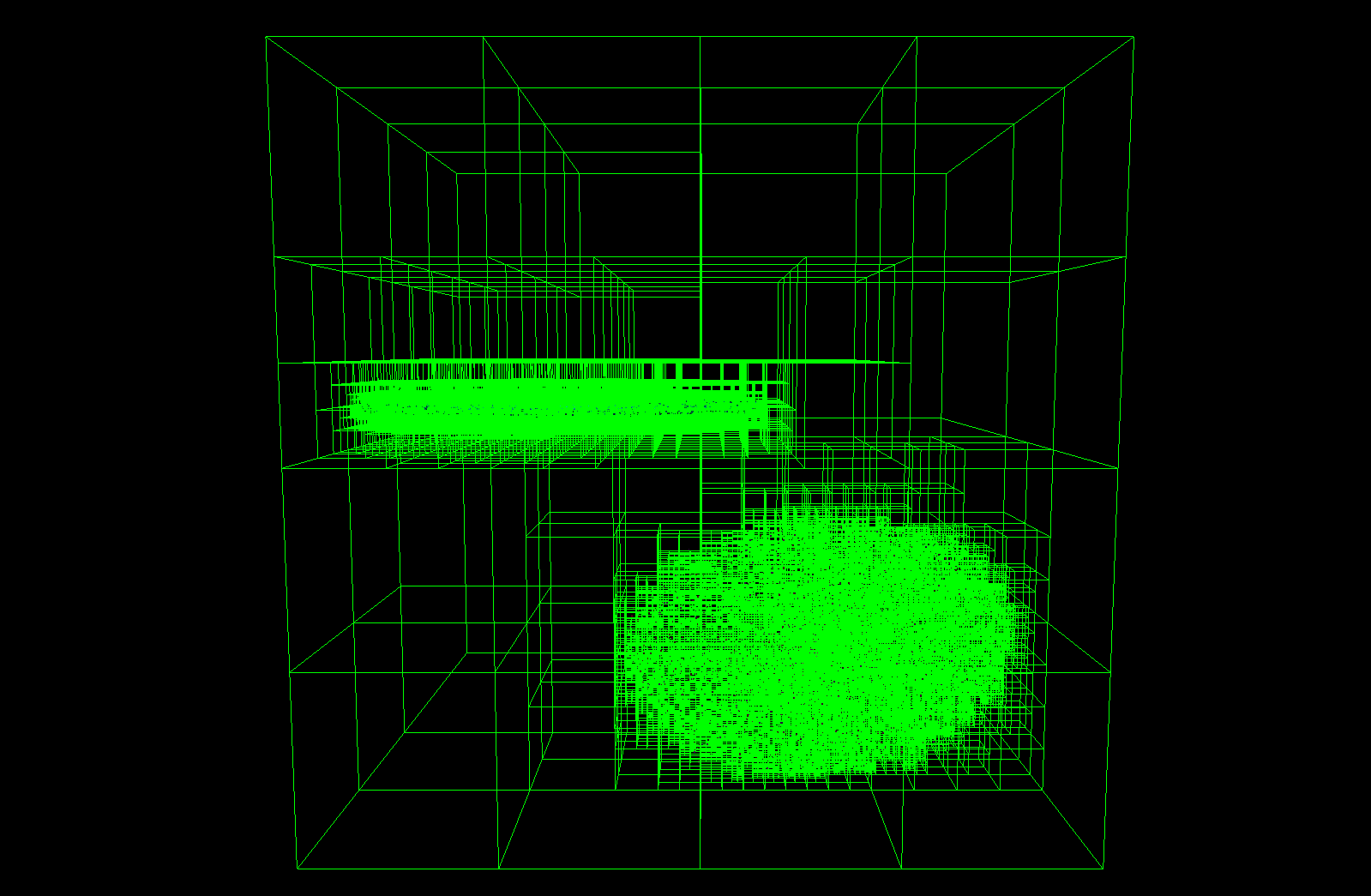
Octree with 20K Bodies

Octree 20K Bodies


Appendix


Libraries Used


Acknowledgements