“Animals do not care about the evolution of the universe. Nor do many humans.”
– Stephen Hawkins

In this lab, we’re going to simulate galaxies using particles.
Please download the lab and go over the code.
When you run the code, you should see some particles. These particles are stationary because the physics code is not yet in place.
In order to be able to run the code with and without OpenGL, we’ll be using the following commandline arguments
> ./Lab08 <RESOURCE_DIR> <(OPTIONAL) INPUT FILE> # WITH OPENGL
> ./Lab08 <#steps> <(OPTIONAL) INPUT FILE> # WITHOUT OPENGLsteps, then the program runs without OpenGL for the specified steps.RESOURCE_DIR, the program runs with OpenGL using the resources in the specified directory.The particle drawing code is already in place. Note the following techniques I am using.
Bill boarding: These are polygons that always face the camera. The vertices of each particle object form a 2D square. Look at the vertex shader. If we transform these vertices as usual with the modelview matrix, these object space vertices will be transformed into camera space, making them rotate and translate as we expect. In order to make them always face the camera, we clear out the rotational (upper 3x3) part of the transformation matrix before we multiply. With this modification, no matter which way the camera points, the square will be rendered face on.
Alpha-blended sprites: Alpha-blending is used to implement transparencies. Look at the fragment shader. We’re taking the alpha value from the provided image file and passing that value as the 4th component of the color. The OpenGL calls to enable alpha-blending are:
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);It doesn’t make sense to use SI units (kilograms, meters, seconds) when we are simulating galaxies. Instead, we’ll be using the following units:
With these carefully chosen units, the gravitational constant, \(G\), which is 6.6732e-11 in SI units, conveniently becomes 1.0, as shown below. This not only helps with numerical scaling but also saves some floating point operations.
[G] = [length] * [velocity]^2 * [mass]^-1
G = 6.6732e-11 * (3.0856776e19)^-1 * (3e5)^-2 * (2.092774335733466e10 * 1.98855e30)
= 1.0For reference:
For each particle, \(i\), the total force is a summation of all the forces from all other particles.
\[ \bar{f}_i = \sum_{j \ne i} \, \frac{G m_i m_j}{(\| \bar{r}_{ij} \|^2 + \varepsilon^2)^\frac{3}{2}} \bar{r}_{ij}, \]
where \(\bar{r}_{ij} = \bar{x}_j - \bar{x}_i\) is the vector between the two particles, and \(\varepsilon\) is the “softening length,” which helps us avoid the singularity when two particles coincide. If we set \(\varepsilon = 0\), we obtain the exact solution. Note that we can remove \(G\) from the equation because we’re using our special “galaxy” units.
We’ll be using the Symplectic Euler integrator.
\[ \begin{aligned} v^{(k+1)} &= v^{(k)} + h m^{-1} f(x^{(k)}),\\ x^{(k+1)} &= x^{(k)} + h v^{(k+1)}. \end{aligned} \]
When computing the forces, make sure to compute all the particle forces before updating any of their positions. In other words, you should not compute the force for a particle and then immediate update the particle’s velocity and position. Instead, you need to compute all the forces for all the particles, and then proceed to update the particle’s positions and velocities.
To test your code, start with the following test cases involving just two stars. Use \(\varepsilon^2\) = 1e-4.
The initial velocity of the light star determines the shape of the orbit. The equation we’re going to use is:
\[ y = \sqrt{G M \left( \frac{2}{r} - \frac{1}{a} \right)}, \]
where \(G\) is 1.0 because of our use of “galaxy” units, and \(M\) is the mass of the heavy star. First, let the distance between the stars, \(r\), be 1.0, and the length of the semi-major axis, \(a\), also be 1.0. This will give us a circular orbit. Using \(h = 1.0\), after 100 time steps (326 million years), the two positions should be
(0.00199442, 0.00324596, 0)
(-0.99442, -0.0836833, 0)If we set \(a\) to be 2.0, we get an elliptical orbit, and after 100 time steps, the positions should be
(0.00213728, 0.00218499, 0)
(-1.13728, 1.688, 0)You should show these numbers to me before moving on to the next task.
Add support for saving/loading the initial conditions. The file format should be the following:
<n> <h> <e2>
<mass> <position> <velocity> <color> <radius>
<mass> <position> <velocity> <color> <radius>
<mass> <position> <velocity> <color> <radius>
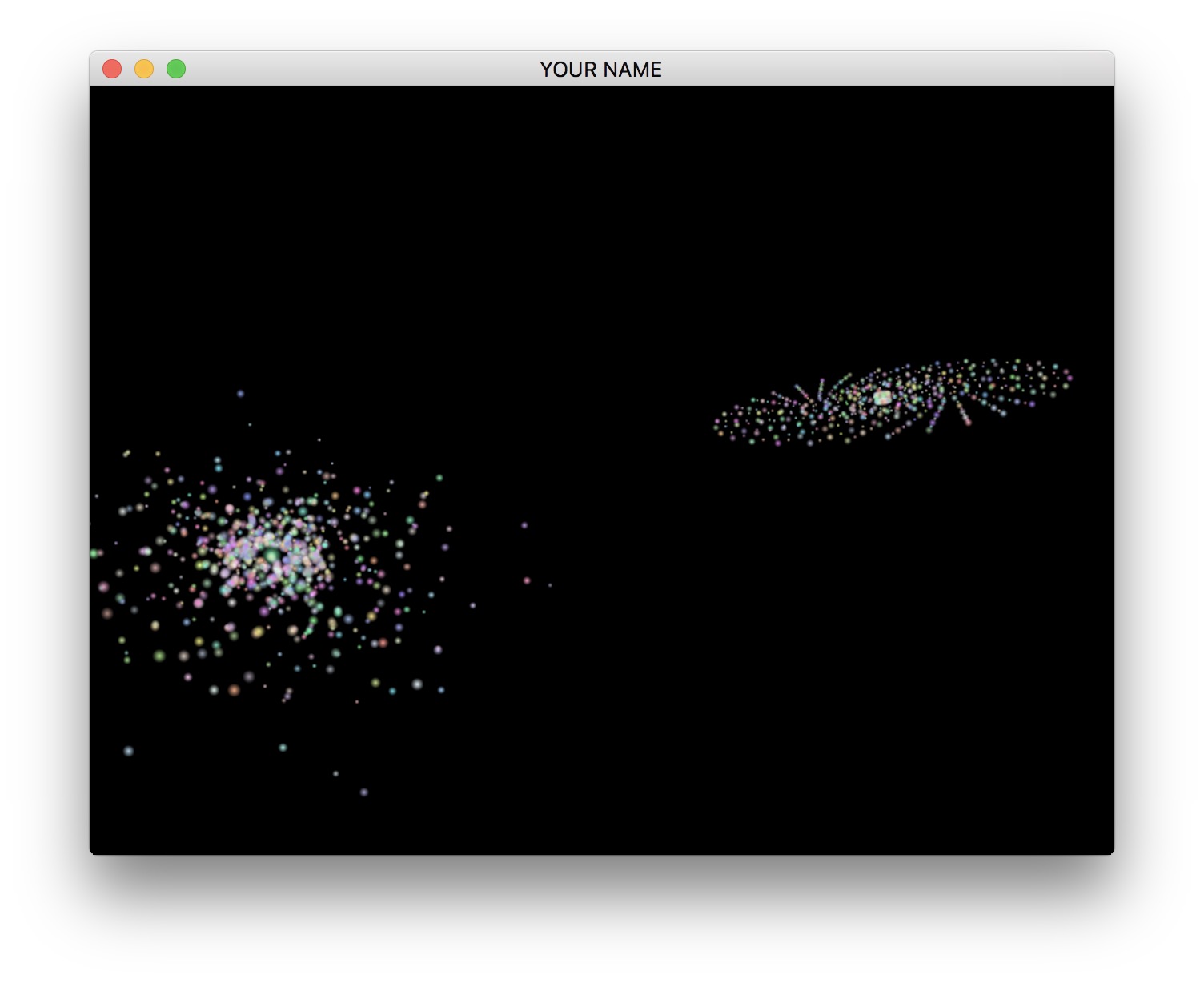
...n is the number of particles.h is the time step.e2 is \(\varepsilon^2\), the square of the softening length.To test your code, try loading the text file in the resource folder. Create an interesting scene of two (or more) galaxies colliding. We will pick one from the class to use as the test case for the parallel computing project.
Make sure your code also works in release mode. You should be able to simulate 1000 particles easily. The easiest way is to use ccmake.
ccmake .. from your build directory.CMAKE_BUILD_TYPE to Release.make -j8.With the provided collide1231.txt input file, after taking 100 steps, the first two particles should have the following positions.
(-1.79806, -0.493514, 0.00107882)
(-1.73418, -0.552937, -0.0752332)The elapsed time should be 652308 years.
You can try out more predefined galaxies. You may need to parallelize your code or use more advanced techniques, such as Barnes-Hut.