In this lab, we’re going to linearly interpolate between two rigid transforms.
Please download the lab and go over the code. Note how I am drawing the axis at the origin using old-school OpenGL.
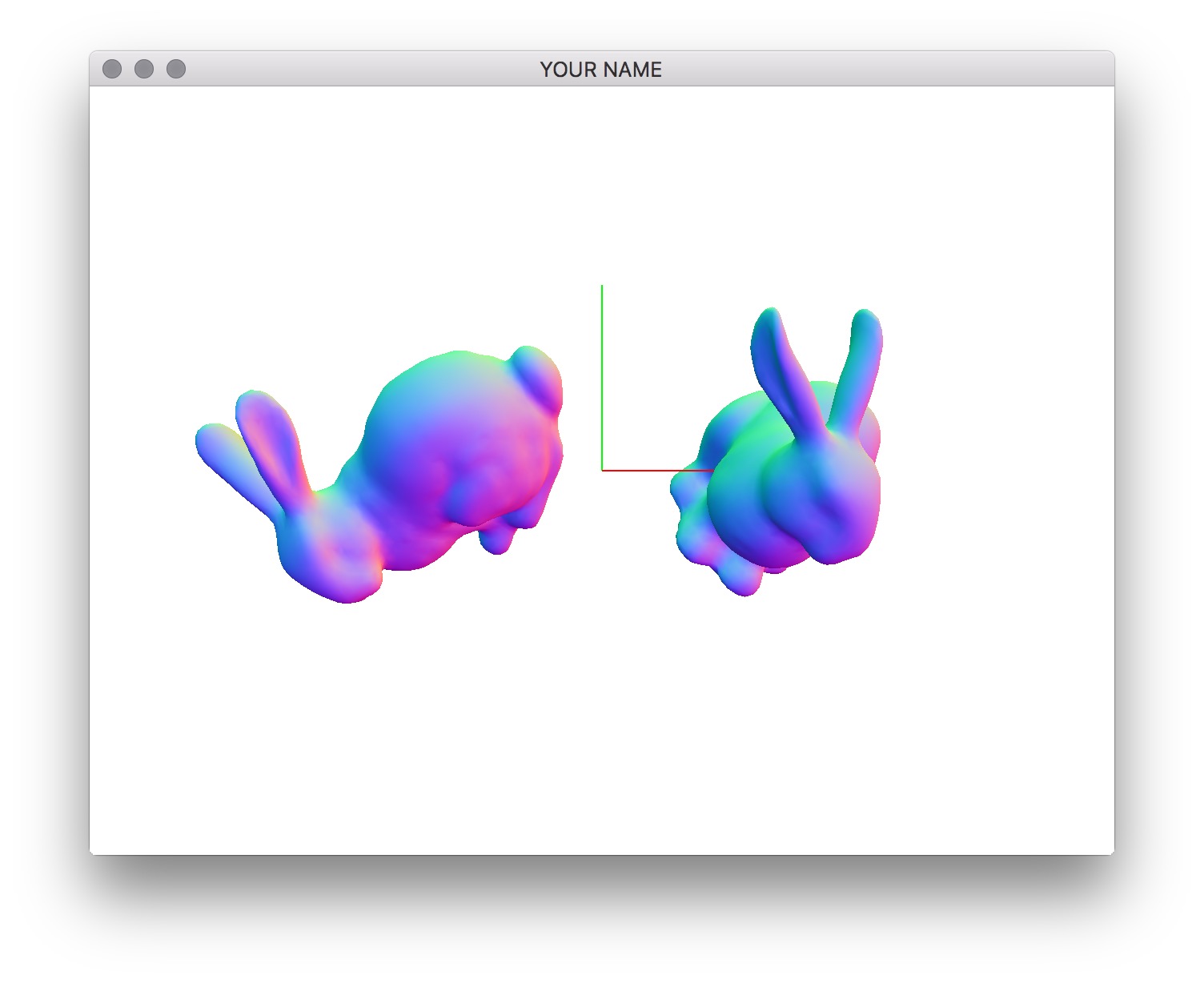
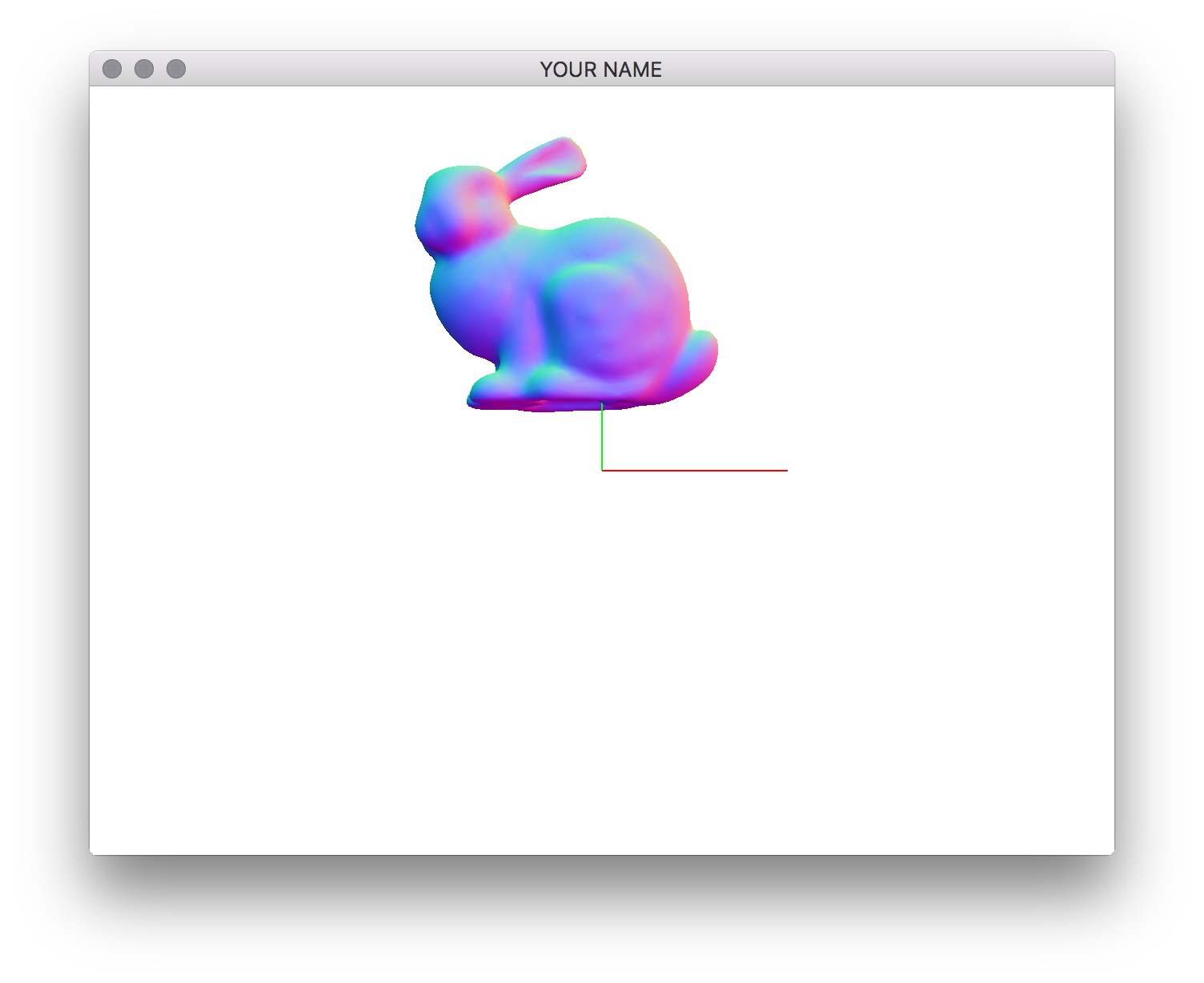
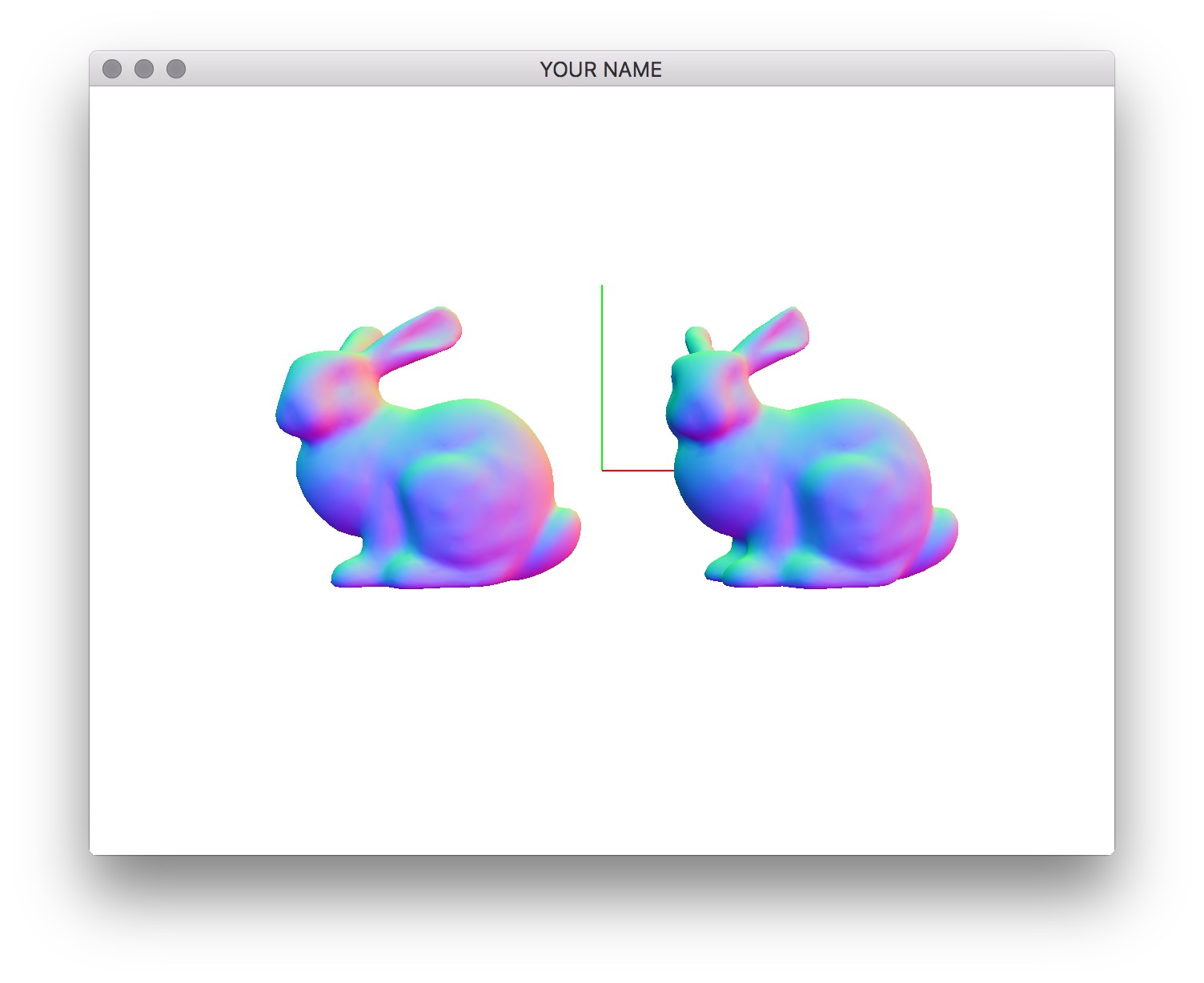
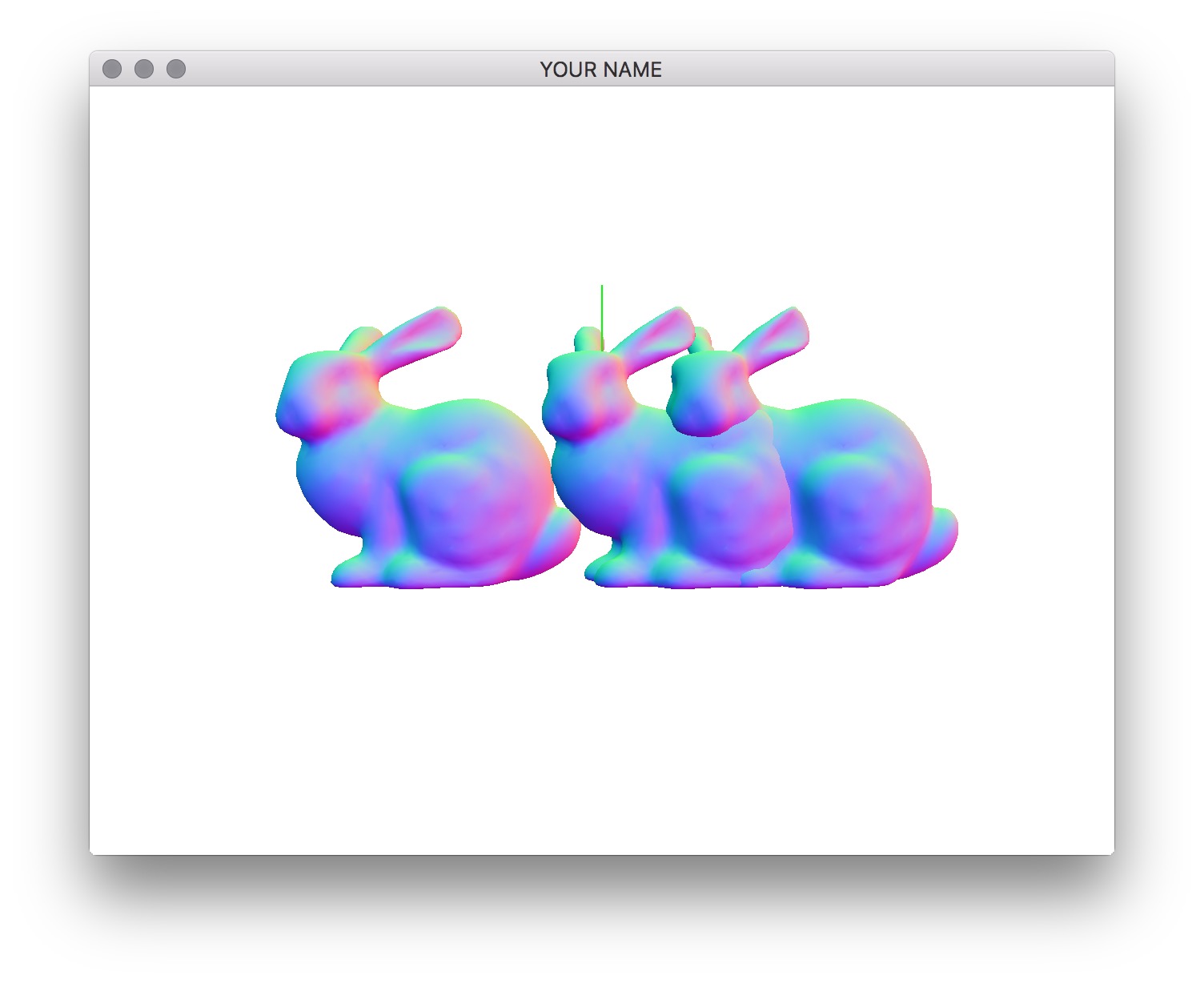
When you first run the code, you’ll see a bunny. However, it is not centered at the origin. (That’s just how the vertex positions in bunny.obj were defined. In general, when you download a mesh file from the Internet, there is no guarantee that the origin is at the center of the object.) The center of this bunny is at (-0.2802, 0.932, 0.0851). Use the center variable in the code to place the bunny at the origin. To do this, you should use the translate() function of the MatrixStack class by calling MV.translate(). Use the provided positions, p0 and p1, to draw the LEFT and RIGHT bunnies. Remember to use MV.push() and MV.pop() appropriately. Then use the provided alpha variable to draw a linearly interpolated bunny.
\[ p = (1 - \alpha) \cdot p0 + \alpha \cdot p1. \]
You should see a bunny translating between the source and target bunnies.



The two quaternion variables, q0 and q1, define the rotations of the source and target bunnies. Note how they are being constructed from axis angles. The first quaternion corresponds to a rotation by \(+90^{\circ}\) about axis0, and the second quaternion is \(+90^{\circ}\) about axis1. Use these quaternions to rotate the two bunnies. You can create a rotation matrix in glm as follows:
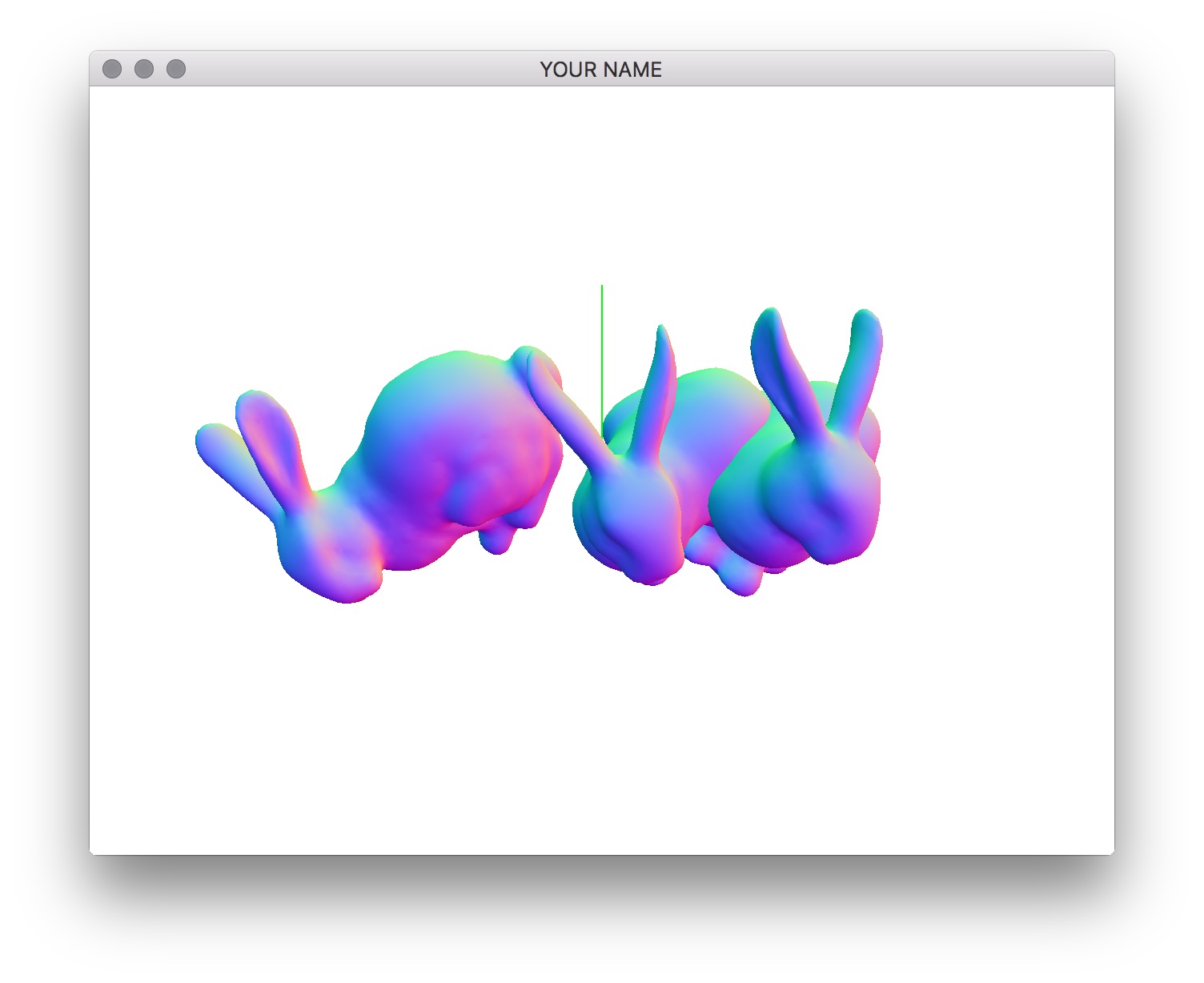
glm::mat4 R = glm::mat4_cast(q0);Use the resulting 4x4 matrix, R, to modify the top element of the matrix stack by calling MV.multMatrix(). Now you should be able to press the x, y, z, X, Y, and Z keys to rotate the two bunnies. Each bunny should rotate about its center point. The lowercased letters change the axis of rotation of the source bunny, and the uppercased letters change the target bunny. Now add rotation interpolation by linearly interpolating the four components of the left and right quaternions, and then normalizing the result.
R = glm::mat4_cast(glm::normalize((1.0f - alpha)*q0 + alpha*q1));Summary: In this code, we’re using three different representations of 3D orientations. First, we use axis angle, since it is the most intuitive geometrically. Then we convert this into a quaternion, since we are interpolating. Finally, we convert this into a matrix so that we can apply it to the matrix stack.