In this lab, we’re going to create pretty graphics with a particle system.
Please download the lab and go over the code.
We are using a C++ library called Eigen. You’ll have to install this
in the same way you installed glm in lab 0. You’ll
need to create a new environment variable called
EIGEN3_INCLUDE_DIR that points to the Eigen directory. Once
you have it installed, you may want to look at this quick tutorial.
OPTIONAL READING: Note the following techniques I am using to draw the particles.
GL_POINTS. These points
are drawn as “billboarded” quads. To control the size of each quad that
gets generated from each point, I am writing to a special output called
gl_PointSize in the vertex shader. This feature,
GL_PROGRAM_POINT_SIZE is enabled in main.cpp.
Click here
and here
for more information.alpha.jpg. For each
“billboarded” quad, the texture coordinates of the fragments are
automatically computed by OpenGL and stored in a special varying
attribute called gl_PointCoord. Then, any texture can be
applied to GL_POINTS. The classic approach to enable alpha
blending requires sorting the particles from back to front, but here I
am using another approach that does not require sorting. Click here
for more information.Vector3f, then
copying this data one by one into an OpenGL buffer would be very
wasteful. Instead, I store the particle position as a
Eigen::Map<Eigen::Vector3f>, which allows me to
define an Eigen::Vector3f that is mapped to a specific
location in a vector<float>. This allows me to
directly update the 3 floats in the buffer. Click here
for more information.Run the code: press the space bar and watch a never-ending sequence
of explosions. This is a 3D explosion — you can rotate the scene with
the mouse as before. Also, try increasing the number of particles by
modifying init(). On my laptop, I can easily go up to
10,000 particles.
Change the Particle::rebirth(...) function so that more
things are randomized appropriately. Use the
randFloat(low, high) function to choose some values you
like. Play around with some values to get an intuition on what these
parameters do.
x (initial position): Where the particle starts
from.v (initial velocity): How fast and in which direction
the particle is moving initially.d (viscous damping): How quickly the particles lose
energy (implemented later).lifespan: How many seconds each particle lives. Once a
particle dies, its rebirth() function is called.You may also change the color and the size of the particles by modifying the constructor.
Currently, each particle moves in a straight because the physics has
not been fully implemented. Modify Particle::step() to do
the following:
Accumulate force: First, we’ll only have the force of gravity.
Create a \(3 \times 1\) vector
f and set it to be the force of gravity using the gravity
vector passed into the function from main.cpp: \[
\vec{f} = m \vec{g},
\] where \(m\) is the mass of
the particle. We’ll add more forces later in this lab.
Integrate velocity: \[ \vec{v}_{\text{new}} = \vec{v}_{\text{old}} + \frac{h}{m} \vec{f}. \]
Integrate position: \[ \vec{x}_{\text{new}} = \vec{x}_{\text{old}} + h \vec{v}_{\text{new}}. \] This line is already implemented for you.
This scheme is called Symplectic Euler integration. Keep in mind that
x, v, and f are all \(3 \times 1\) vectors.

You should try running your code in release mode (See lab 0) so that you can simulate more particles.
We can easily add other types of forces by changing Step 1 from the previous task. First, add viscous damping force:
\[ \vec{f} = −d \vec{v}, \]
where \(d\) is the viscous damping
coefficient. (This force does not replace the force of gravity. You
should add them up since we want both.) This applies a negative force
proportional to the velocity of the particle. Try changing
d to see what values look good. Don’t make this value too
large, or else you’ll run into numerical problems.
The force of gravity we have implemented so far assumes that the
force of direction is constant everywhere. (This is the assumption we
usually make on the earth’s surface.) Now we’ll add another type of
gravity that is more general. Use keyToggles[’g’] to toggle
between these two types of gravity. The new gravity force follows the inverse
square law. The force magnitude falls off as the inverse square of
the distance. We’ll use the world origin to measure the distance. We’ll
use the softened
version of the force, which was developed by astrophysicists so that
division by \(0\) does not occur when
the orbital distance becomes too small.
\[ \vec{f} = -\frac{C m}{\left( \| \vec{x} \|^2 + \varepsilon^2 \right)^\frac{3}{2}} \vec{x}, \]
where \(C\) is a constant you
choose, \(m\) is the mass of the
particle, \(\vec{x}\) is the position
of the particle, and \(\varepsilon^2\)
is the “softening length,” which you should set to a small number, such
as 0.01f. Play with \(C\)
and \(\varepsilon^2\) to get a sense of
what they do.
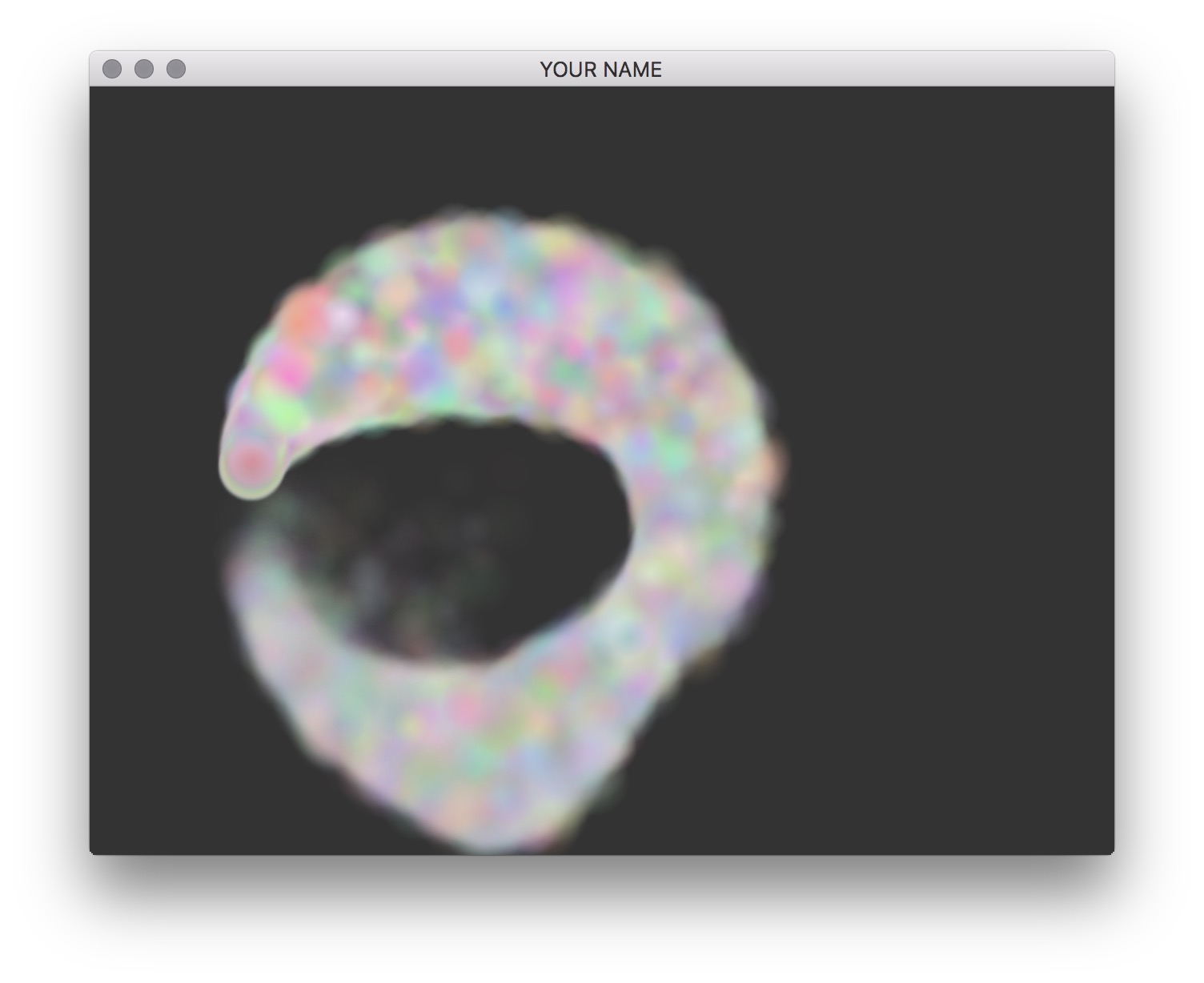
Add collision with the floor (the \(y=0\) plane) to the end of
Particle::step(). If you detect that the particle is below
the floor, set its position to be at the floor and flip its velocity
with respect to the floor. The particle’s tangential velocity should
remain fixed, while its normal velocity should be flipped. Add a toggle
for this with the f key.