Heuristic Methods for IK

Aaron Su

CSCE 450

Introduction

The traditional method of IK optimization requires optimizing n individual link-angles (𝛉1, ..., 𝛉n), which involves optimizing a high-dimensional parameter space, leading to high computational complexity and potentially long optimization times.

The Circular Alignment Algorithm (CAA) streamlines the optimization process for an n-link, equal-length articulated arm by focusing on a single parameter -- the subtended angle 𝛃 -- when aligning the arm along a circular arc. This approach is more efficient than optimizing for the individual n link-angles (𝛉1, ..., 𝛉n) because it significantly reduces the dimensionality of the optimization problem. By representing the arm's configuration using a single parameter, the algorithm simplifies the search space, making it easier and faster to find the optimal alignment.

Further, the Cyclic Coordinate Descent (CCD) algorithm employs a heuristic approach to expedite the inverse kinematic process. CCD focuses on updating one joint angle at a time, iteratively adjusting each angle to improve alignment with the desired end-effector position. By iteratively addressing each joint in a cyclic manner, CCD effectively narrows down the optimization space, reducing the overall dimensionality of the problem. This targeted and sequential adjustment of joint angles contributes to a more rapid convergence towards a solution.

The problem of Inverse Kinematics (IK) on an n-link articulated arm is highly under constrained with many possible solutions. While analytical solutions exist and are achievable for few-link arms, as n increases, analytical solutions soon become unscalable. Thus, many numerical solutions have been widely used in the computer graphics and robotics industry.

In this project, I explore the characteristics of Circular Alignment Algorithm (CAA) and Cyclical Coordinate Descent (CCD) on an N-link, equal-length, articulated arm. All methods are implemented from scratch and evaluated across a standard set of movement challenges in a 2d simulation.

Implementation

The baseline IK and CAA were both optimized using BFGS with max iterations 150, tolerance 1e-6, max line-search iterations 20, and gamma 0.5.

While the baseline IK objective function aims to minimize the distance from the target (with theta regularization), the CAA objective function minimizes the difference between local and global alignment parameterized by an angle 𝛃.

CCD, which does not rely on optimization, uses a threshold distance of 0.1. While traditional CCD adjusts from link n to link 1 for each iteration, I found that minimizing the number of links involved in the optimization problem reduced computational costs. More specifically, I used the distance from the target to each link to find the minimum last k links needed to reach the target, assuming all previous links remain in the same position. This is denoted by CCD* in charts and diagrams.

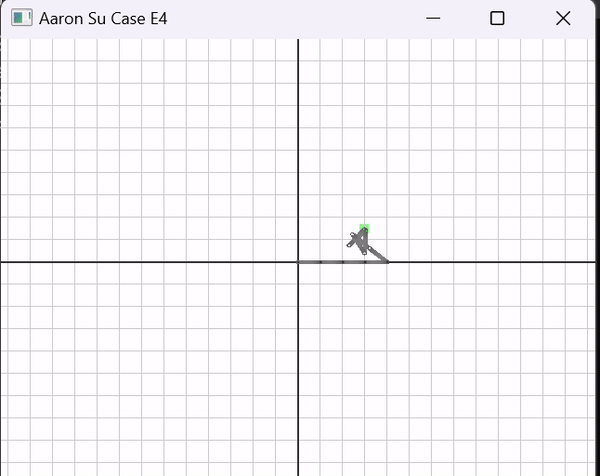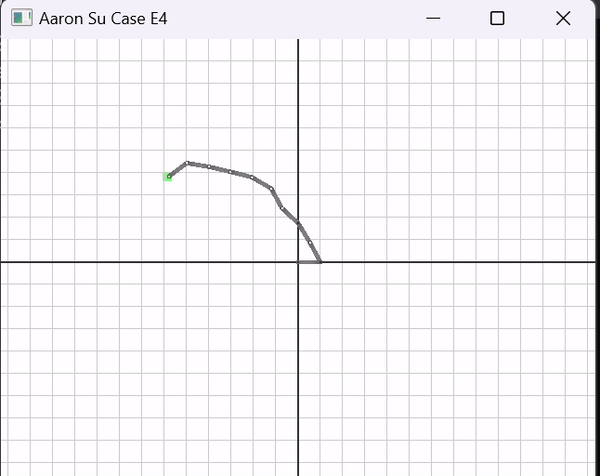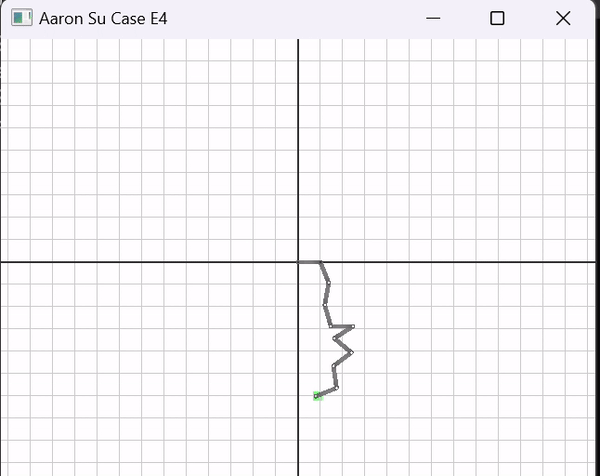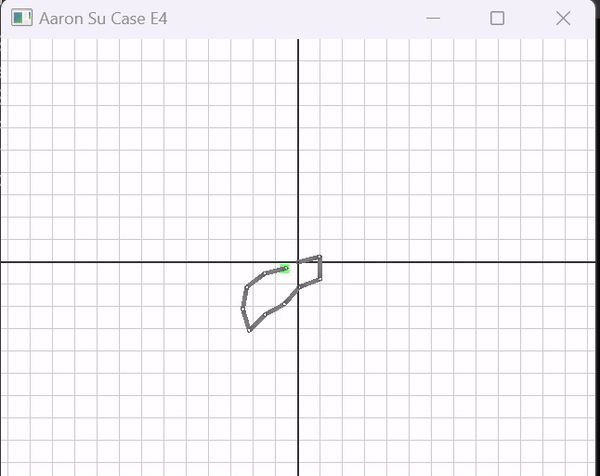
All IK methods were evaluated on a suite of 4 simulations using 4-links and 10-links. Simulation 1 follows a horizontal line. Simulation 2 follows a box centered around the origin. Simulation 3 is a circle centered around the origin, and Simulation 4 is a figure-8 (See Simulations).

Findings

To discuss findings, we should first discuss measures of proximity and iterations. While one could argue that the proximity to target is mostly dependent on the tolerance set in the optimizer, I attempted to balance iterations with proximity for each method and found that reducing tolerance did not greatly decrease the number of iterations for convergence.

Further, each iteration requires different amounts of computation. For example, each iteration for Baseline IK requires much more computation than for CAA due to the number of parameters optimized. On the other hand each iteration of CCD contains n angle adjustments, and each iteration of CCD* contains between 2 and n* angle adjustments. Overall, the iteration count should be used as a proxy for “computational efficiency”, and not as the end goal.

As expected, the Baseline IK was closest to the target for all simulations.

Furthermore, the fastest converging method varied between CCD*, CCD, and CAA. This depended on the simulation and number of links. When evaluating proximity and iteration count, CCD* was the best, with consistently low distance-to-target and low iteration counts.

Proximity and Iteration Counts

CCD* Denotes CCD which optimizes the last k links required to reach the target.

Relative Iteration Counts

Simulations

Simulation Plots

Resources / Works Referenced

Andreas Aristidou, Joan Lasenby, FABRIK: A fast, iterative solver for the Inverse Kinematics problem, Graphical Models, Volume 73, Issue 5, 2011, Pages 243-260, ISSN 1524-0703, https://doi.org/10.1016/j.gmod.2011.05.003.

Aristidou, A., Lasenby, J., Chrysanthou, Y. and Shamir, A. (2018), Inverse Kinematics Techniques in Computer Graphics: A Survey. Computer Graphics Forum, 37: 35-58. https://doi.org/10.1111/cgf.13310

Canutescu, A.A. and Dunbrack, R.L., Jr. (2003), Cyclic coordinate descent: A robotics algorithm for protein loop closure. Protein Science, 12: 963-972. https://doi.org/10.1110/ps.0242703

Buss, S. R. (2004). Introduction to inverse kinematics with jacobian transpose, pseudoinverse and damped least squares methods. IEEE Journal of Robotics and Automation, 17(1-19), 16.