

A project by Alexander Gonzales
With a lot of inspiration from Legend of Zelda: Wind Waker, I decided do create an ocean-themed
simulator, where a boat travels to random locations by pressing a key.
Relevant techniques used: A* pathfinding, B-splines, and spherical linear interpolation
The scene contains a series of island meshes that act as obstacles, with an ocean entity
mapping over the nodes the boat can travel over to reach a designation.
The ocean was created using aspects of the cloth class from Assignment 5, where we can create
a grid with a flexible number of rows and columns.


The grid comprises of an array of nodes arranged in an equal number of rows and columns, similar to the setup of the cloth from Assignment 5. Every node in this grid contains the following variables:
The x and z axes will always be kept constant throughout the program runtime, but
but will oscallate on the y-axis to simulate a wave.
In the main program file, two of these nodes will be labeled as a "start" and "end"
point, which will be used in the A* class to calculate the best route between these
two points.
The pathfinding algorithm utilized in this program is A* search. Here we
have a square grid, that may contain obstacles, and starting from one node
we want to get to the target node as quickly as possible.
In every step A* takes, it picks up the node that has the lowest f-cost, which
is a variable in a struct that equals the sum of two other parameters – g-cost
and h-cost.
To get the distances for the g and h costs, we use the getDistance() function, which use the grid, the start point, and the end point as the parameters. In the algorithm, we use an open and closed list, which indicates which nodes are available in proximity to the start node (from GeeksforGeeks):

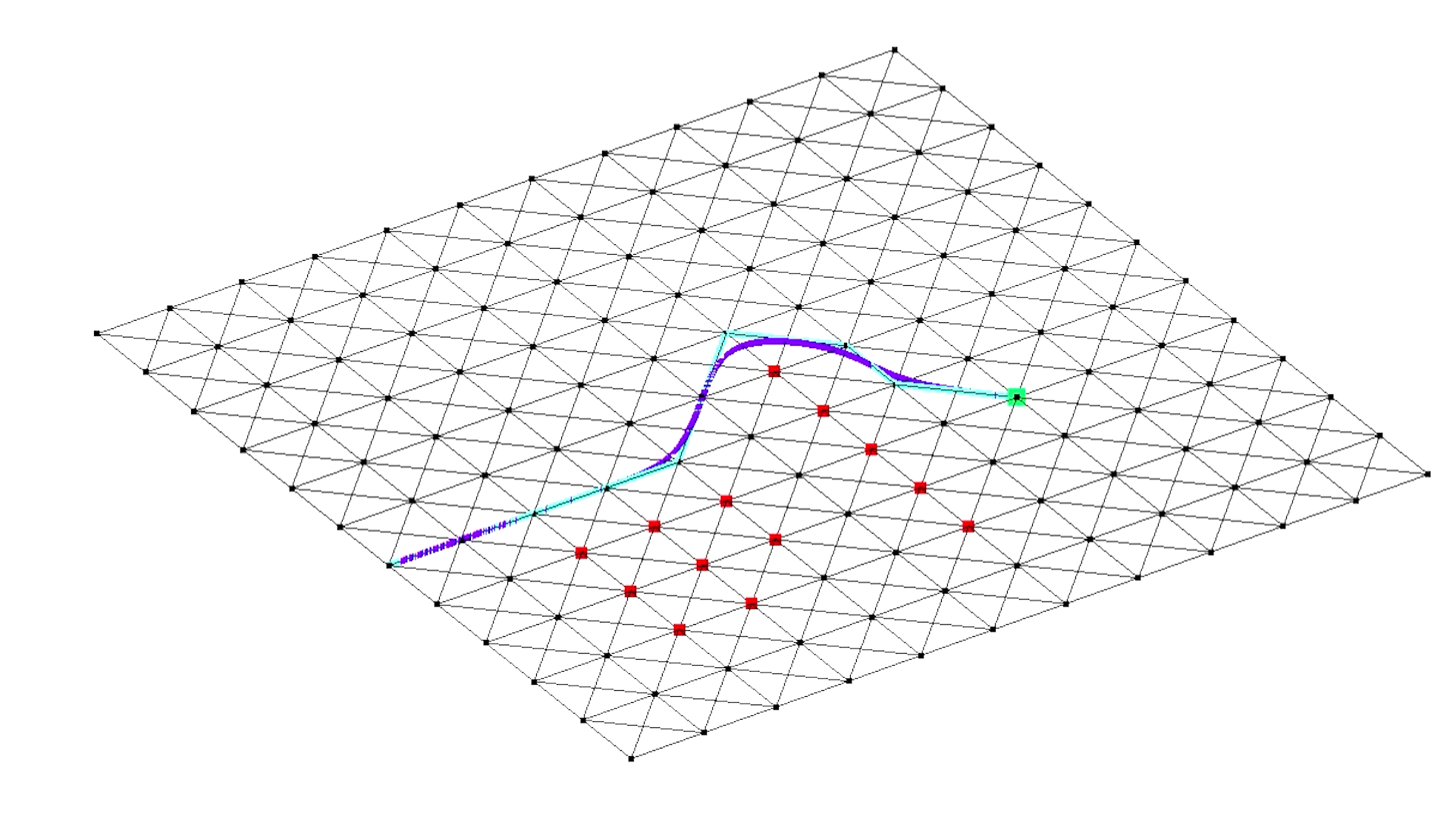
Now that we have a list of nodes that tracks the path from the start to end nodes, we can make a secondary path that draws out a smoothed path using cubic spline curves. To do this, for every node in the path we draw a curve using four points (if we have less than 4 control points the boat will linearly interpolate directly to the end point). We can do this by using the following formula:
We want the boat to move in relation to the wavelike movement of the nodes, so we set the G matrices' positions to the x value of the nodes. By doing this, and changing the basis matrix to create a B-sline, we can make the boat move in a curved path to its location. We can then animate the boat to travel to its location by using spherical linear interpolation.
Alexander Gonzales | 12/12/2022 | CSCE 450 - Computer Animation