In this lab, we will explore transformation matrices and practice transforming (translating, scaling, and rotating) objects. We will not be using GLM (a linear algebra library) today but will be implementing all matrix functions ourselves. We’ll try out GLM in the next lab.
NOTE: This lab is very tedious, since it requires you to create the matrices yourself by putting in the 16 correct numbers into each 4x4 matrix. For the assignments, you will be using GLM and matrix stacks, so Lab 4 will be more practical.
Please finish Lab \(0\). This will set up your development environment for the rest of the semester.
Then, download the code for the lab and go over the code.
We will not be modifying the shaders in this lab, but it might be
helpful to take a quick look at the included vertex shader
(resources/vert.glsl). Note how the vertex colors are
computed from the vertex normals. These normals come from the .obj file.
Also, note that the vertex positions are multiplied by two uniform 4x4
matrices, P and MV. P is the
“projection” matrix, and MV is the “modelview” matrix. By
changing what is passed into the modelview matrix, we can move the
vertices around and thus the object. We will not be modifying the
projection matrix in this lab.
Now look at main.cpp. Note how we are loading an .obj
file with the vertex normals and not just vertex positions. In the .obj
file, the normals are specified using the vn lines.
Also note in main.cpp how we’re using STL maps to store
attribute, uniform, and buffer IDs. This makes the code a little cleaner
with fewer global variables. It is a good idea to think of ways to write
wrappers for various parts of the program.
Without any modifications, the program does not draw anything,
because the 4x4 modelview matrix is initialized to zero in
render().
Implement createIdentityMatrix() to load the identity
matrix. OpenGL uses column ordering, which means that the elements of
the 4x4 matrix are stored in a one-dimensional array
(float A[16]) using the following indexing scheme: \[
\begin{pmatrix}
0 & 4 & 8 & 12 \\
1 & 5 & 9 & 13 \\
2 & 6 & 10 & 14 \\
3 & 7 & 11 & 15
\end{pmatrix}.
\] To access the \((i,j)^{th}\)
element, you should use A[i+4*j]. For debugging, you can
use the printMatrix() function.
This function, and others you implement in this lab, should set all 16 components of the matrix, even if they are zeros. In other words, assume that the input matrix has garbage values in them.
Now, if you call createIdentityMatrix() before passing
in the matrix to the vertex shader (i.e., before
glUniformMatrix4fv()), you’ll see something like this.

Because the default camera is at the origin looking down the z-axis,
you’re inside the cube, and you’re seeing the back side of the cube.
Implement createTranslationMatrix() and move the cube back
in the negative z direction by a few units. Remember that this function
creates a translation matrix and returns it in the 1st argument. It
should not translate the input matrix. Once you have it implemented,
call the function instead of createIdentityMatrix(), and
you should see the front of the cube.
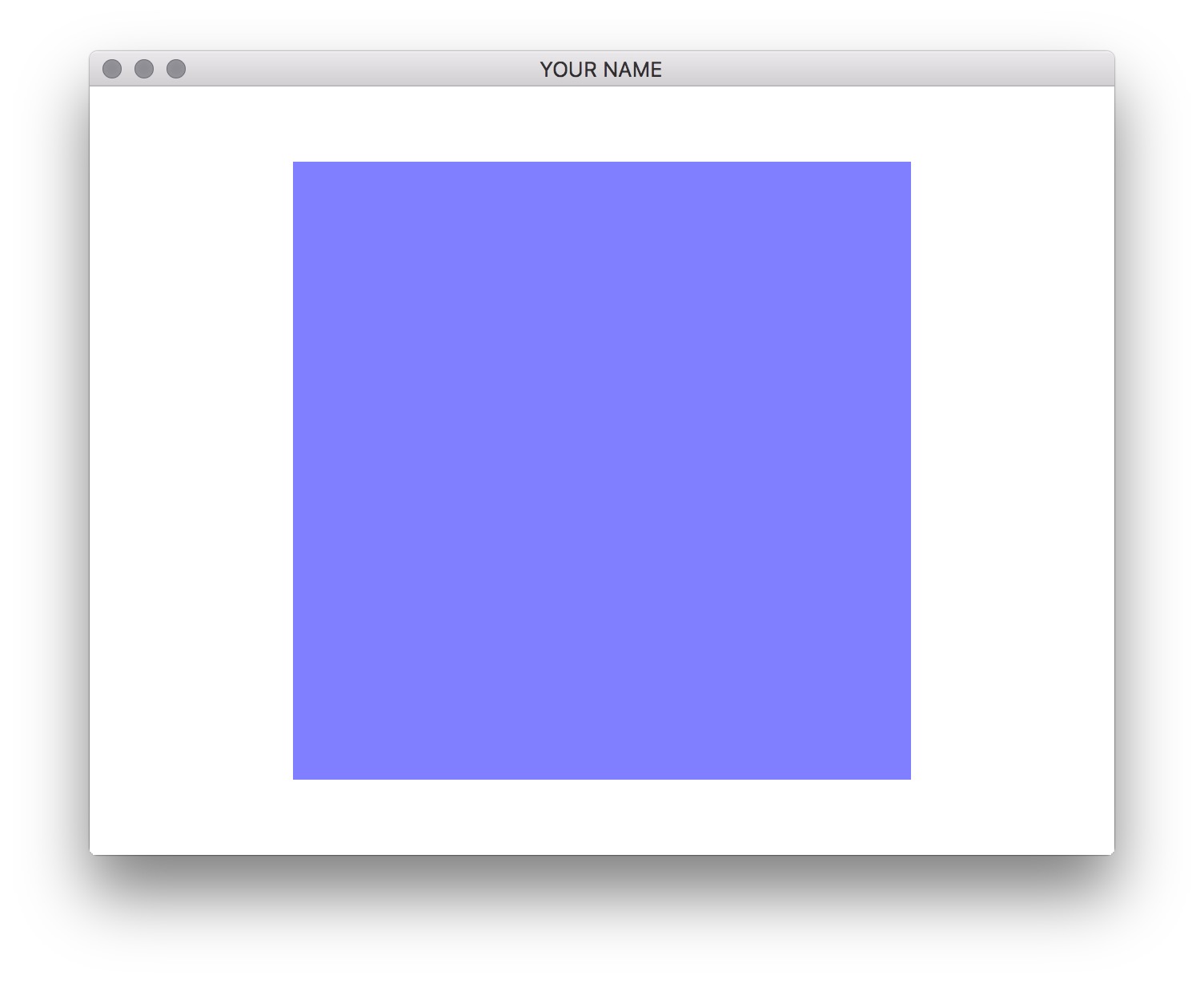
Now you’re seeing the front of the cube. Each face has a different color because we’re using the normal to set the color in the vertex shader.
Implement multMatrix(). To test your matrix multiply
code, try this simple test case:
float A[16], B[16], C[16];
for(int i = 0; i < 16; ++i) { A[i] = i; }
for(int i = 0; i < 16; ++i) { B[i] = i*i; }
multMatrix(C, A, B);
printMatrix(A, "A");
printMatrix(B, "B");
printMatrix(C, "C");The output should be:
A=[
0.00 4.00 8.00 12.00
1.00 5.00 9.00 13.00
2.00 6.00 10.00 14.00
3.00 7.00 11.00 15.00
];
B=[
0.00 16.00 64.00 144.00
1.00 25.00 81.00 169.00
4.00 36.00 100.00 196.00
9.00 49.00 121.00 225.00
];
C=[
144.00 976.00 2576.00 4944.00
158.00 1102.00 2942.00 5678.00
172.00 1228.00 3308.00 6412.00
186.00 1354.00 3674.00 7146.00
];Note that you cannot use the same matrix as both input and output. In
other words, this will not work: multMatrix(A, B, A) or
multMatrix(A, A, B).
Implement createScaleMatrix(),
createRotationXMatrix(),
createRotationYMatrix(), and
createRotationZMatrix(). Using multMatrix(),
you can compose transformations together. If you move the cube away from
the camera and rotate by 0.5 radians about the y-axis, you should see
this.
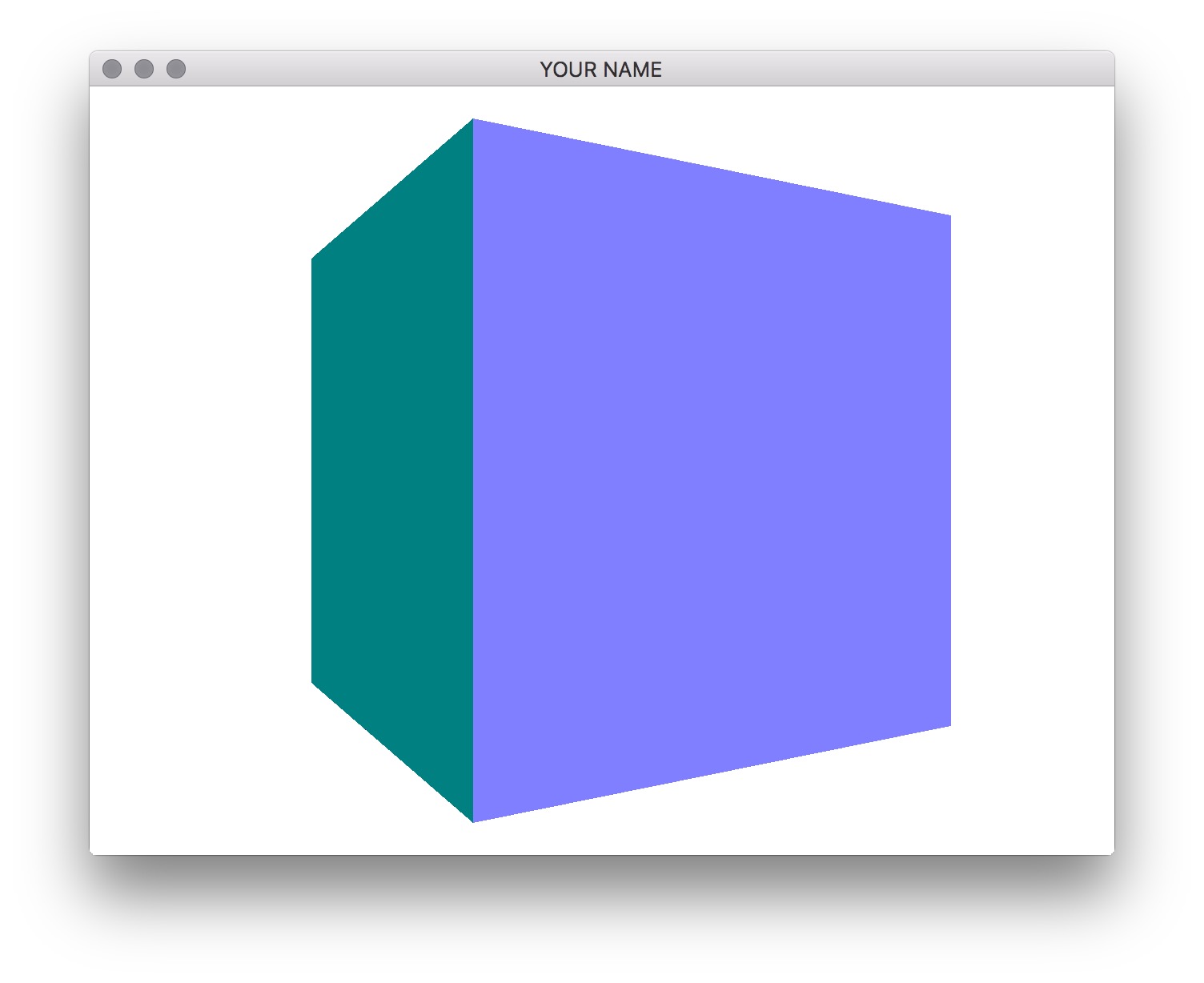
The order of matrix multiplication is really important! Make sure you understand how this works.
Create the letter A by drawing a transformed cube three times. In
order to do this, you’ll have to call glUniformMatrix4fv()
and glDrawArrays() three times. For example, to create the
left side of A, you need to scale, rotate, and translate the cube. (The
order of these three transformations is important!) Your result should
look something like this.

How would you rotate the letter as a whole, so that it looks like this?
