Home

Assignment 2 — Hierarchical Transforms

Due Wednesday 2/21 at 11:59 pm. You must work individually.

Goals

Learn and apply hierarchical 3D transformations using the matrix stack.

Associated Labs

Overview

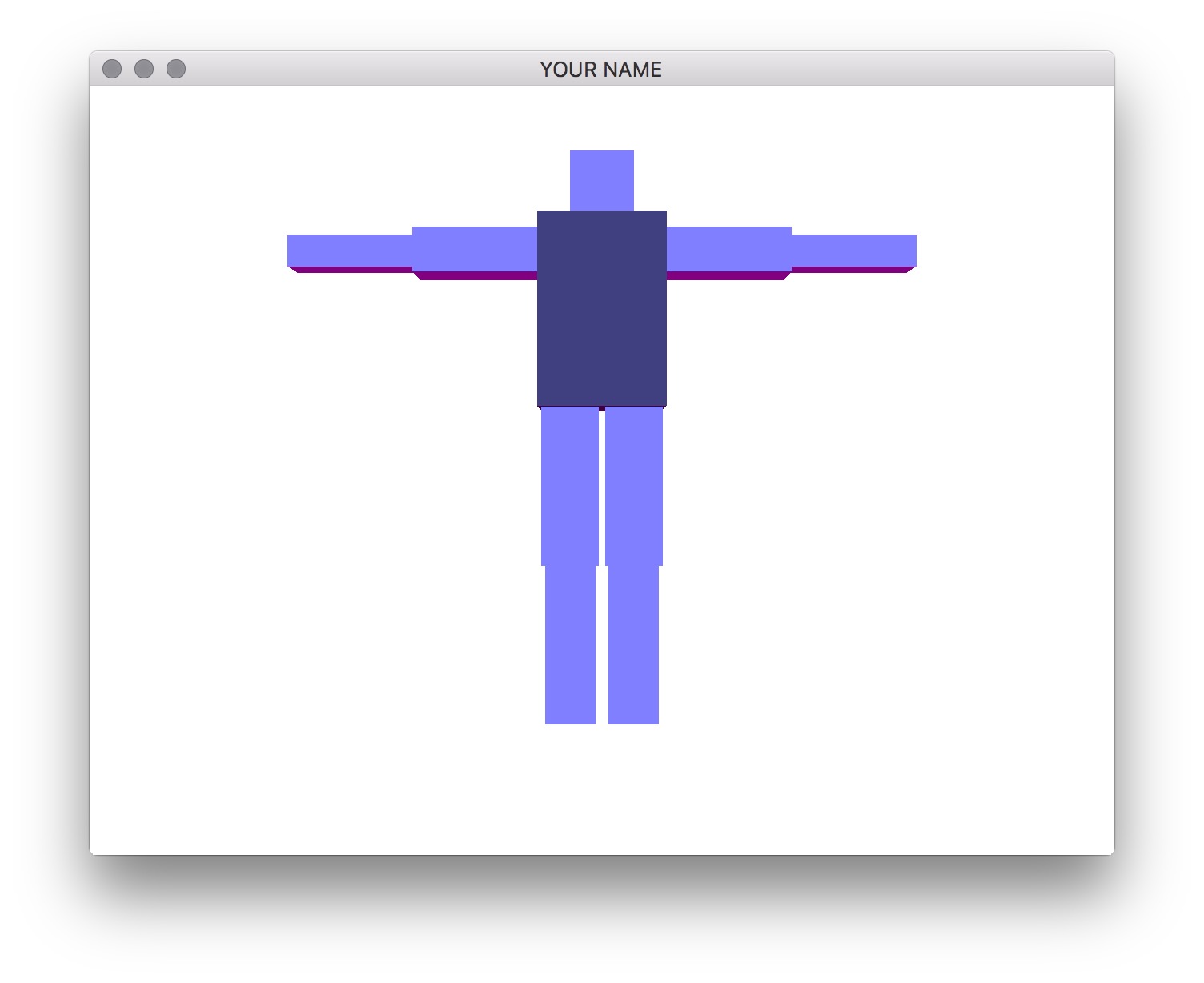
Write a program that allows you to create a robot that you can manipulate with the keyboard. You are free to create your own robotic character, but there should be at least 10 components in the robot, and the hierarchy should not be flat. For example, in the figures below, we have the following hierarchy:

Notes

Task 1: Starting Point

Start from your Lab 0 or Lab 4 code base.

  1. Create your A2 project folder and copy the the lab files and folders into it.
  2. Modify CMakeLists.txt to change the project name (line 4).
  3. Add GLM calls so that you can draw transformed squares. There are two choices:
    1. If you’re starting with Lab 4, then you should already have this done.
    2. If you’re starting with Lab 0, then replace the teapot with a cube and then try transforming it.
      • The benefit of starting with Lab 0 is that it contains the helper classes (e.g., Shape, Program, etc.) to help you organize your code. You will be required to do this for later assignments.
      • This option is slightly harder but will be helpful for doing the bonus.

Task 2: Nonrecursive Hierarchy (optional)

You may skip ahead to Task 3 if you understand how to draw the components recursively. In this task, we are going to draw just the torso and the head without recursion so that you first understand how the transforms chain together.

In your render() function, first draw the torso and the head without any hierarchy:

prog->bind();
glUniformMatrix4fv(prog->getUniform("P"), 1, GL_FALSE, value_ptr(P));
// Draw the torso
MV->pushMatrix();
    MV->translate(...); // Where is the torso with respect to the world?
    MV->rotate(...); // This rotation applies only to the torso
    MV->scale(...); // This scale applies only to the torso
    glUniformMatrix4fv(prog->getUniform("MV"), 1, GL_FALSE, value_ptr(MV));
    shape->draw(prog);
MV->popMatrix();
// Draw the head
MV->pushMatrix();
    MV->translate(...); // Where is the head with respect to the world?
    MV->rotate(...); // This rotation applies only to the head
    MV->scale(...); // This scale applies only to the head
    glUniformMatrix4fv(prog->getUniform("MV"), 1, GL_FALSE, value_ptr(MV));
    shape->draw(prog);
MV->popMatrix();
prog->unbind();

Note: In this pseudocode, I’m assuming that P and MV are matrices. In your code, these may instead be pointers to MatrixStack, in which case you need to call glm::value_ptr(P->topMatrix()). (Don’t forget #include <glm/gtc/type_ptr.hpp>.) Alternatively, you can write &P->topMatrix()[0][0].

The indentation between push and pop helps with clarity but is not necessary. The first call to glUniformMatrix4fv() sends the projection matrix to the GPU. (For this assignment, you do not need to modify the projection matrix.) Then, we modify the modelview matrix, send it to the GPU, and then draw the shape. With this naive version, changing the position or the rotation of the torso does not modify the head.

To fix this, we now add some pushes and pops. Note that when we rotate the torso, we want the head to also rotate, but when we change the scale of the torso, we do not want to change the scale of the head. Therefore, we use an extra push/pop around the torso scale:

...
// Draw torso
MV->pushMatrix();
    MV->translate(...); // Where is the torso's joint with respect to the world?
    MV->rotate(...); // This rotation applies to torso and its children
    MV->pushMatrix();
        MV->translate(0, 0, 0) // Where is the torso's mesh with respect to the torso's joint?
        MV->scale(...);
        glUniformMatrix4fv(prog->getUniform("MV"), 1, GL_FALSE, value_ptr(MV));
        shape->draw(prog);
    MV->popMatrix();
    // Draw head
    MV->pushMatrix();
        MV->translate(...); // Where is the head's joint with respect to the torso's joint?
        MV->rotate(...); // This rotation applies to head and its children
        MV->pushMatrix();
            MV->translate(...) // Where is the head's mesh with respect to the head's joint?
            MV->scale(...);
            glUniformMatrix4fv(prog->getUniform("MV"), 1, GL_FALSE, value_ptr(MV));
            shape->draw(prog);
        MV->popMatrix();
    MV->popMatrix();
MV->popMatrix();
...

With the code above, translating and rotating the torso should also translate and rotate the head. Note that with this hierarchical version, the numbers used for translation/rotation/scale of the head may be different than with the previous non-hierarchical version, since now we are defining the head with respect to the torso.

Task 3: Recursive Hierarchy

Now we are going to create a general, hierarchical structure for drawing a robot with multiple limbs.

Create a class that represents a component. This class should contain the necessary member variables so that you can make a tree data structure out of these components. The root of the tree should represent the torso, which means that transforming the torso transforms everything else.

In addition to the member variables required for the tree hierarchy, the class should also have the following:

The drawing code should be recursive—in other words, in the render() function in main.cpp, there should be a single draw call on the root component, and all the other components should be drawn recursively from the root. In the main render() function, you should create an instance of the matrix stack class and pass it to the root component’s drawing function. Make sure to pass the matrix stack by reference or as a (smart) pointer.

The component’s rendering method should take the current state of the component and draw it. You should not create the robot hierarchy in this method. In other words, the scene setup must be done in main’s init() rather than in main’s render(). In your README, state where in your init() function (which line) should be modified to change the joint angles. (This statement in the README is only required if you’re stopping at Task 3. Once Task 4 is implemented, we do not need to know where these lines are because we can use the keyboard to test your code.)

For this assignment, the 3D rotation of the joint should be represented as a concatenation of three separate rotation matrices about the x-, y-, and z-axes: Rx * Ry * Rz. The position of the joint should not be at the center of the box. For example, the elbow joint should be positioned between the upper and lower arms.

Task 4: Interaction

Add the functionality to select components and rotate the joints with the keyboard. To do so, we’ll be using the glfwSetCharCallback() function. This callback function tells us which character was pressed. You can put the key argument in an if statement or a switch statement:

static void char_callback(GLFWwindow *window, unsigned int key)
{
    switch(key) {
        case 'x':
        {
            // Do something
            break;
        }
    }
}

When the appropriate key is pressed, the currently selected component, along with all of its descendants, should be rotated about the joint. For example, if the upper right arm is rotated, the lower right arm should rotate with it. The keyboard control should be as follows:

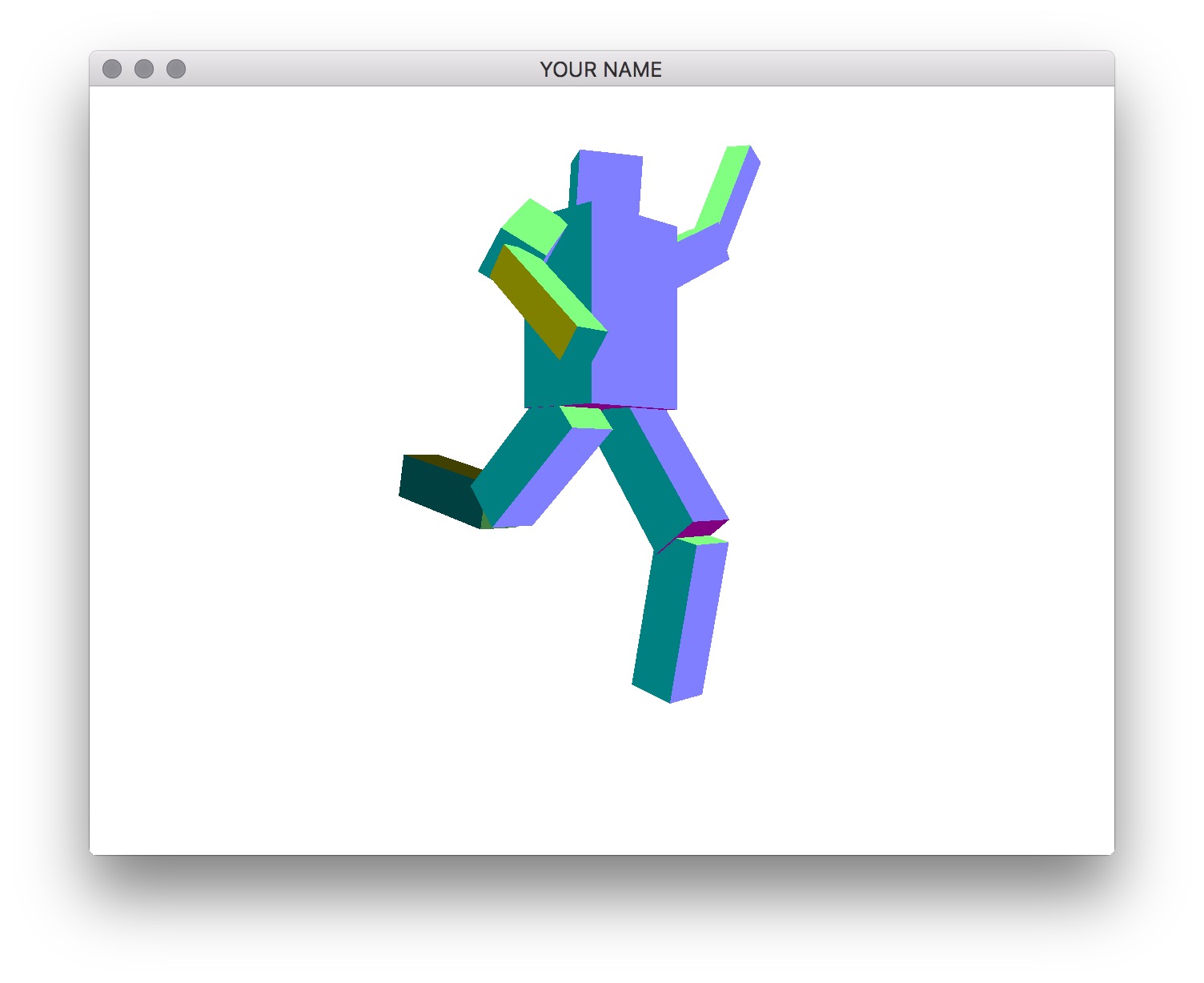
By pressing the period and comma keys, you should be able to select different components in the hierarchy. You must draw the selected component so that it is distinguishable from unselected components. The x/X, y/Y, and z/Z keys should change the rotation angle of the selected component. The traversal of the tree with the period and comma keys should be in depth-first or breadth-first order. Do not hardcode this traversal order—your code should be set up so that it works with any tree.

When drawing the selected component, change its size using the time variable. In the render() function, use the following GLFW call:

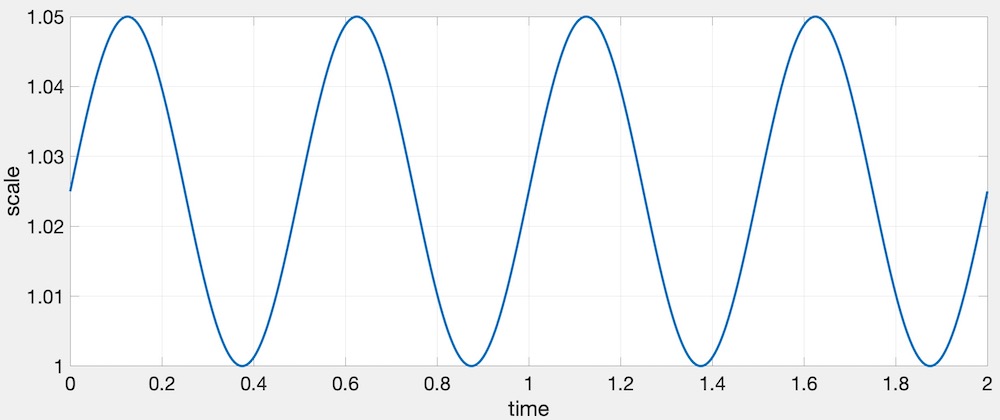
double t = glfwGetTime();

This t variable should then be used to change the scale as follows: \[ s(t) = 1 + \frac{a}{2} + \frac{a}{2} \sin(2 \pi f t), \] where \(a\) is the amplitude, \(f\) is the frequency, \(t\) is the time, and \(s\) is the resulting scale. The following values work well: \(a=0.05\), and \(f=2\). In other words, the scale increases by 5% twice a second. Here is a plot of this function.

Here is a working example:

Task 5: Joint Mesh

Put a cube at each joint. The cube should be placed exactly where the joint is, so that when the joint is rotated, the cube does not translate. These cubes should not be in the hierarchy. Instead, they are extra meshes to be drawn by each component. The total number of components must still be 10 (torso, head, plus 4 limbs with 2 components each).

For bonus, instead of drawing a cube, draw a sphere.

Task 6: Animated Mesh

Rotate at least two components in place. This rotation should not be propagated to its children. At least one of the two should be a non-leaf component.

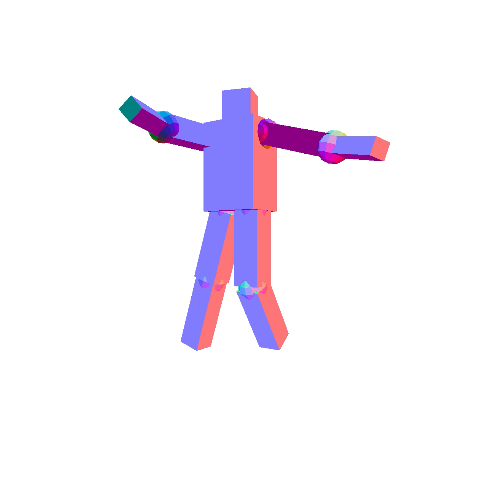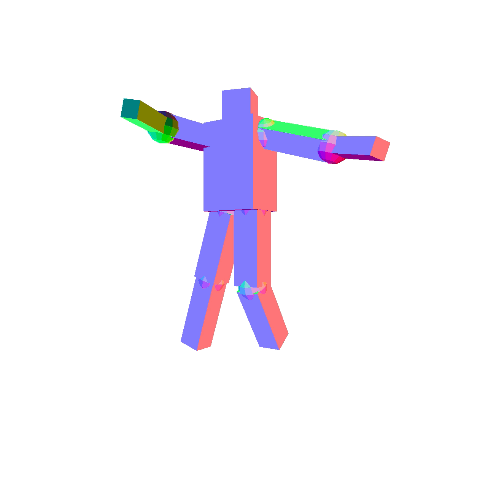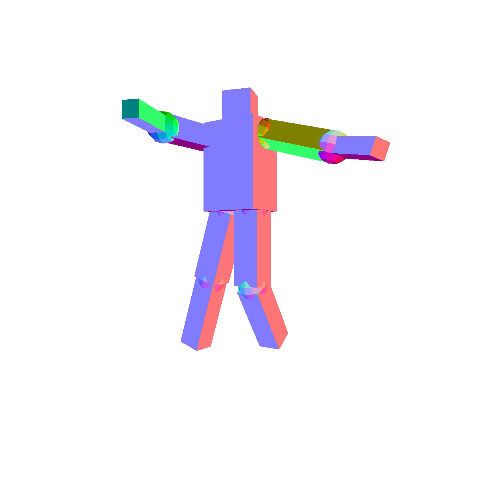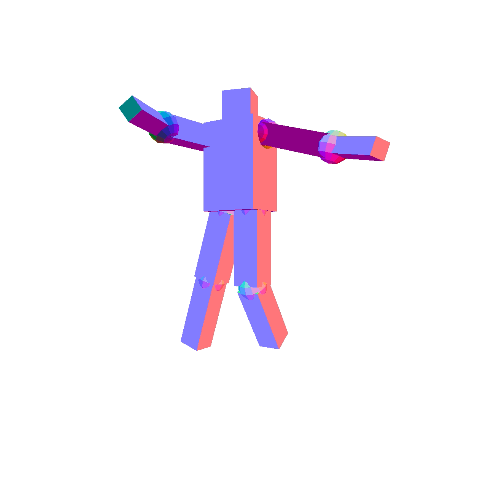
Once rotation is added, it may be difficult to see the selected component. You can ignore this problem, or you can optionally fix it.

HINT: Debugging OpenGL & GLSL

Rubric

Task 2 is optional. If you have completed Task 3, you will get full points for Task 2.

Total: 100 + 5 points

What to hand in

Failing to follow these points may decrease your “general execution” score. On Linux/Mac, make sure that your code compiles and runs by typing:

> mkdir build
> cd build
> cmake ..
> make
> ./A2 ../resources

If you’re on Windows, make sure that you can build your code using the same procedure as in Lab 0.

Generated on Wed Feb 21 10:30:16 CST 2024