Please download the code for the lab and go over the code.
In this lab, we will alter an existing program in order to get started working with OpenGL, GLFW, and GLSL. Your goal is to be able to add two new colored triangles to the scene and to make one vertex of one triangle be repositioned based on a mouse click.
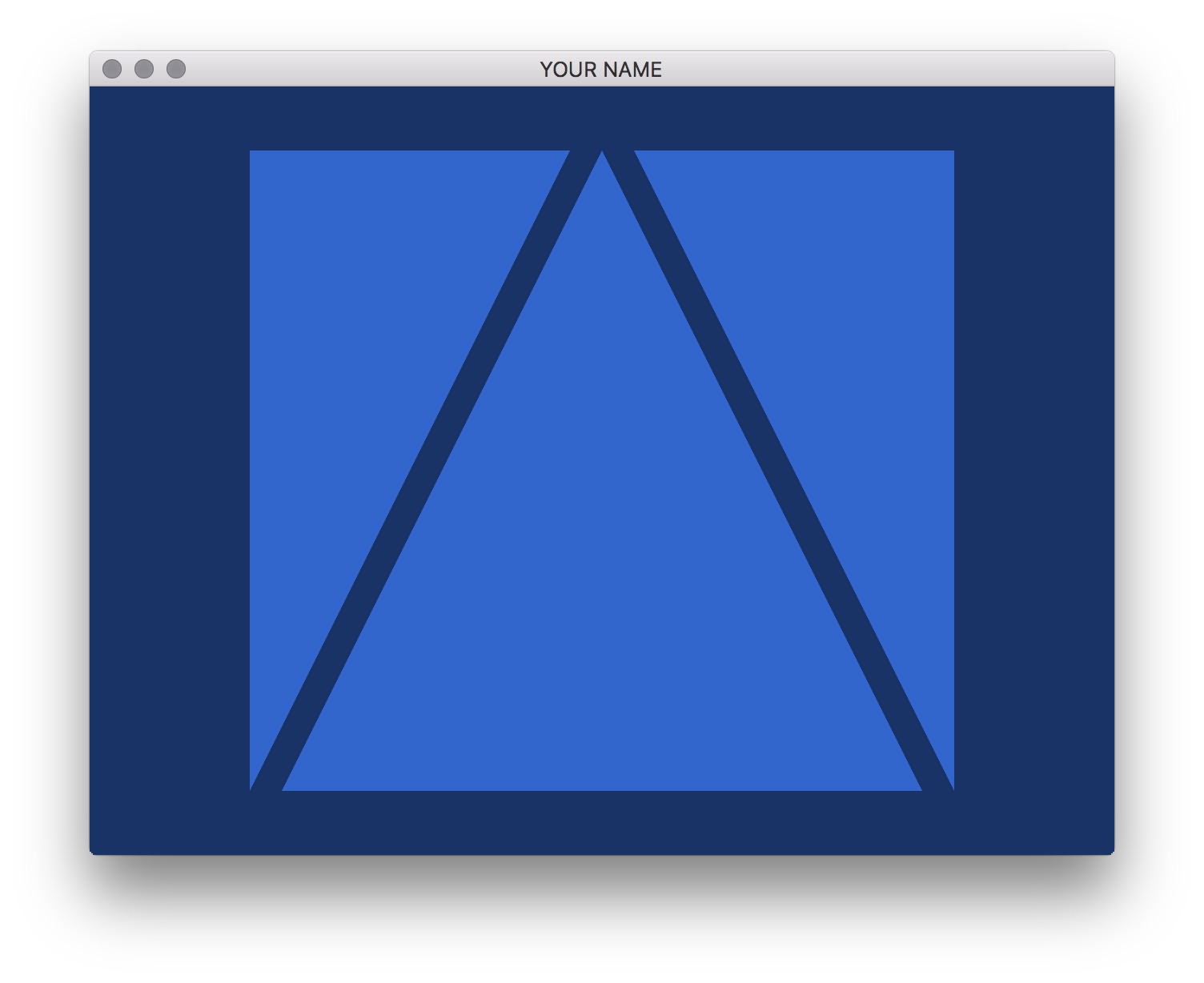
Modify the code to add two other triangles to the scene. You will do this by modifying main.cpp only. You will have to make modifications in init() as well as a small modification in render(). (Look for the hard-coded number 3.) Then modify the fragment shader to draw blue triangles, so it should look as follows:

Note that the colors is of type float, and so the R, G, and B values should be in the range 0.0 to 1.0.
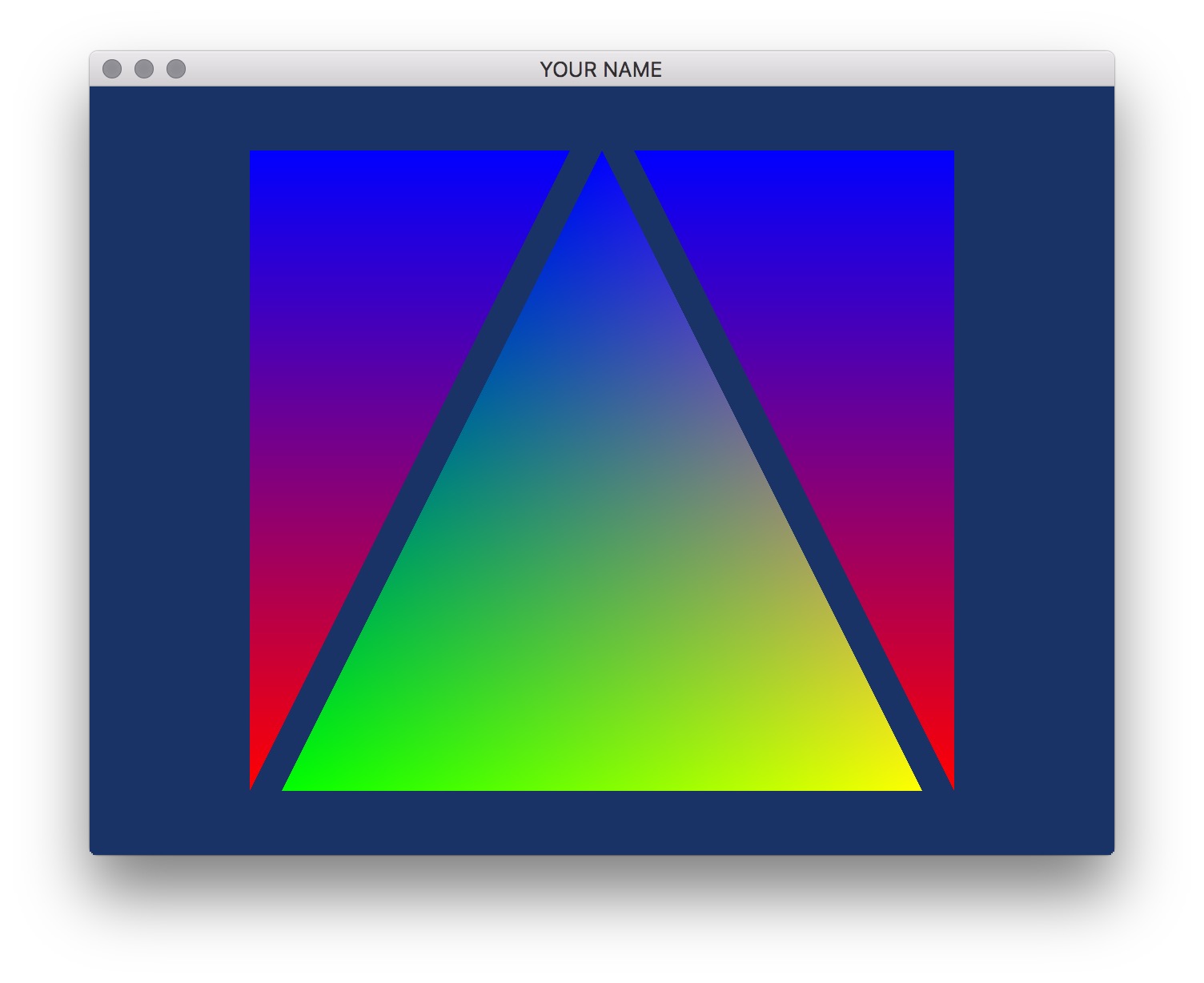
Further modify the code to pass in a different color per vertex. For this, you will need to modify the .cpp file, the vertex shader, and the fragment shader. In the two shaders, you’ll need to add a new varying parameter, which is an output of the vertex shader and an input of the fragment shader. In the vertex shader, this parameter should simply pass through the incoming color. The fragment shader can then use this color to assign the final color of the fragment. The result should look something like this:
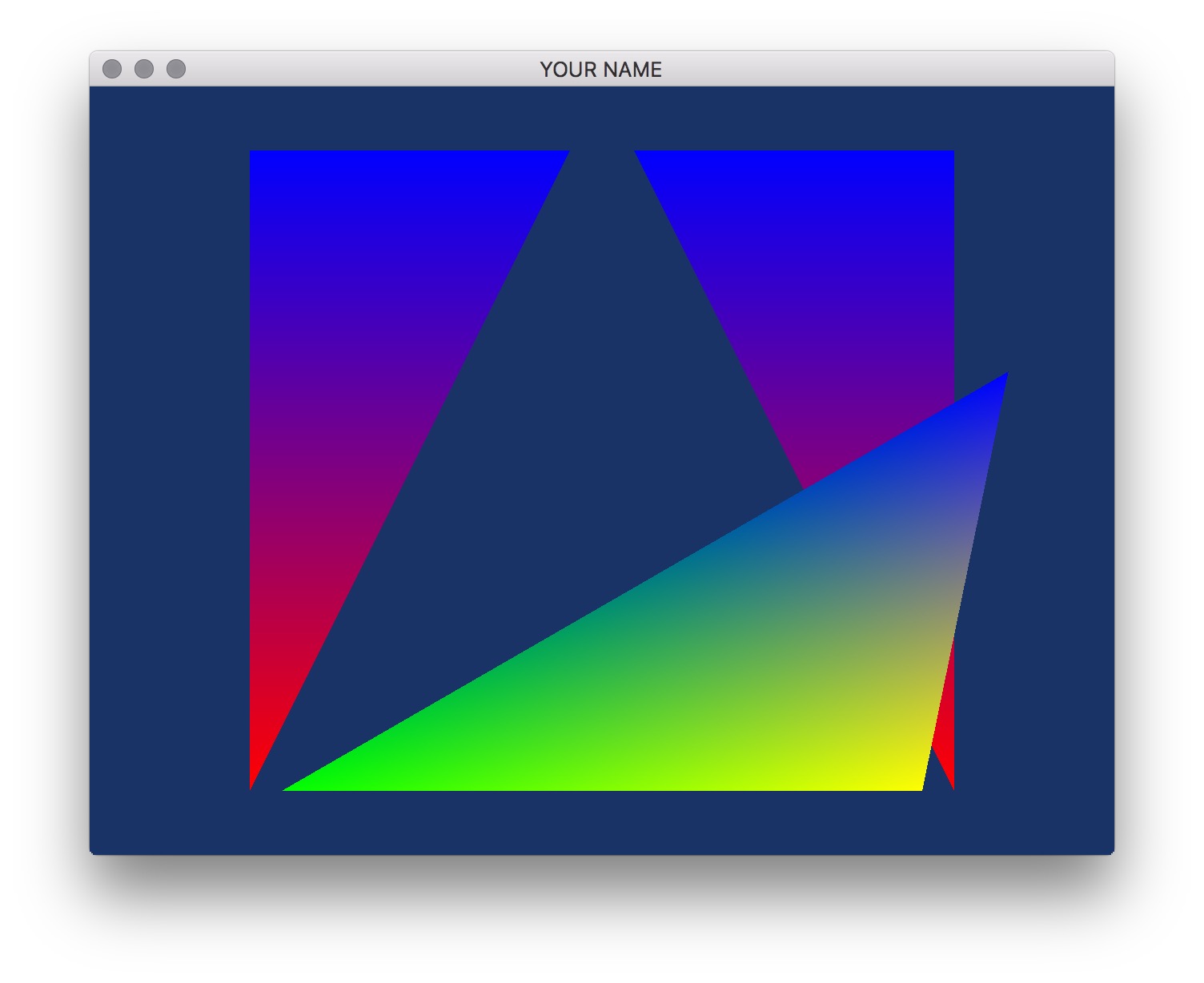
Take a look at mouse_callback() in main.cpp. Using the variables xMinWorld, xMaxWorld, yMinWorld, yMaxWorld, width, and height, compute the world coordinates of the mouse cursor. Currently, the lab code sets this to be 0:
newPt[0] = 0;
newPt[1] = 0;Replace these two lines with the result of your computation.
This transformation is very similar to how we transform world coordinates to image coordinates. Here, we want to go backwards: from image coordinates to world coordinates. The equations are:
\[ \begin{eqnarray} x_w &= s_x x_i + t_x,\\ y_w &= s_y y_i + t_y. \end{eqnarray} \]
There are two slight differences:
With these conditions, the parameters are:
\[ \begin{eqnarray} s_x &= \frac{\Delta x_w}{width},\\ s_y &= \frac{\Delta y_w}{height},\\ t_x &= \text{min}(x_w),\\ t_y &= \text{min}(y_w). \end{eqnarray} \]