Camera manipulation using splines.
Details
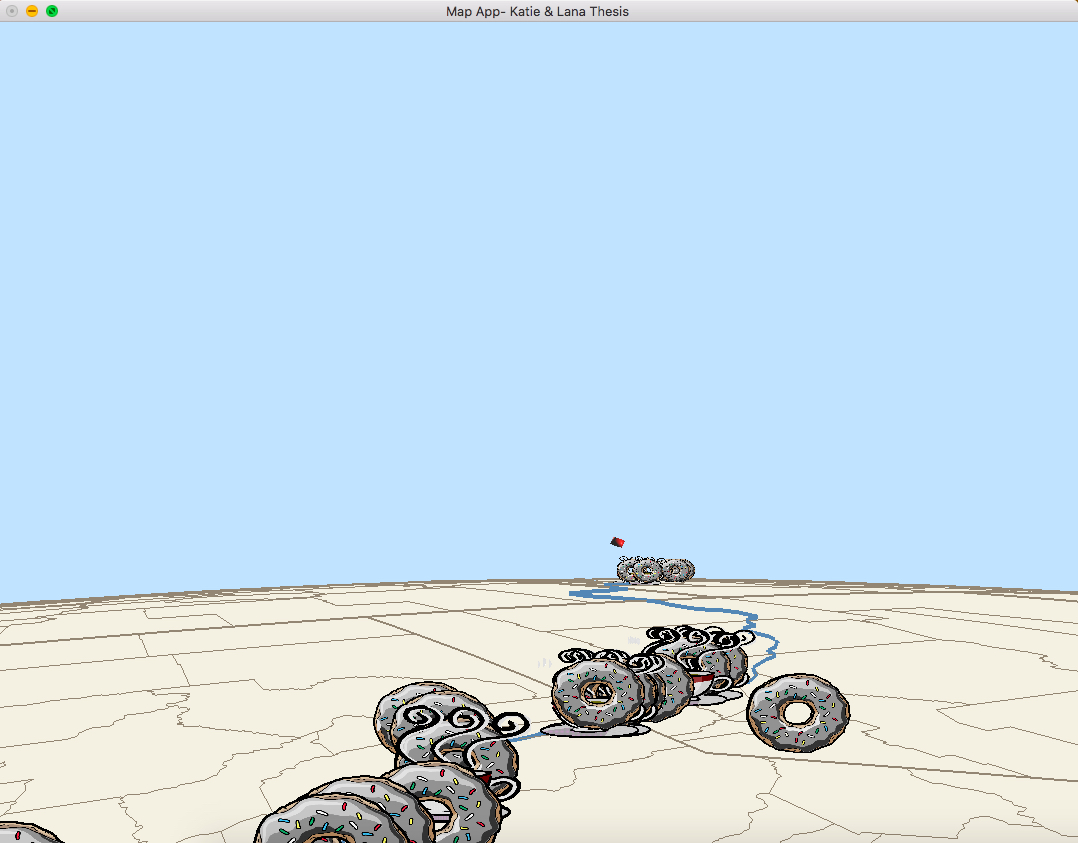View of the map from the Spline Camera
All the graphics for this project are generated using OpenGL. The donuts and coffee cups seen throughout the map are sprites (textures drawn to the screen) rendered as billboards to always face the camera. The camera follows a B-spline created from the points along the path. A lookAt function is used to create the view matrix. The function takes in the position of the camera (eye), the position where the camera is looking at (lookAt), and the up direction for the camera (up). To change the camera lookAt different keystrokes could be used, the following section explains how to manipulate the camera.
How to Maneuver the Scene
- space bar - Start the spline camera
- t - Set the target of the lookAt to be the middle of the path
- 0 - Set the target of the lookAt to be San Francisco, CA
- 1 - Set the target of the lookAt to be San Luis Obispo, CA
- 2 - Set the target of the lookAt to be Pleasanton, CA
- 3 - Set the target of the lookAt to be Denver, Colorado
- 4 - Set the target of the lookAt to be Portland, Oregon
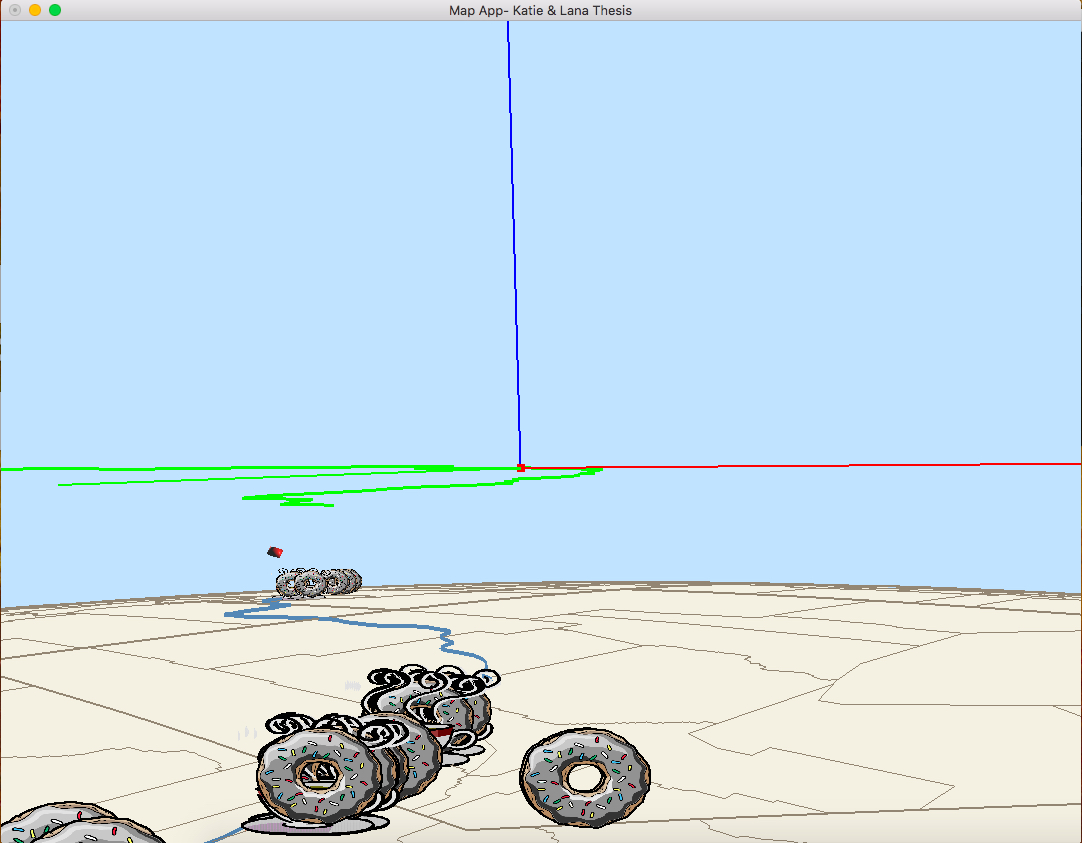The green line is the spline generated. The red dot is the current position along the spline. The origin frame is drawn to ensure that the tangent, binormal, and normal are being computed properly at the current position.
Movement along the Spline
Initially the camera followed along the spline (the green line in the image above) at exactly the position (the red dot and frame). The lookAt is always set to be a small distance along the current tanget of the frame, so as the tangent changed through very curvy areas of the path and spline, the movement was too much to handle for the user's eye. Another issue was that the up vector was being set to merely a vector in the positive z direction. This is because of the way the world was rotated to view the U.S., z pointed in the up direction. This, however, is not satisfactory as the up vector depends on the position along the spline. Part of this problem came from the fact that a new path is generated each time the map is created, based on the source and desination given by the user. Because of the new generation of the path each time, key frames could not be created for the path to ensure that the pitch and yaw of the camera is being interpolated correctly between positions along the spline. In order to do this dynamically, I compute the tangent, binormal and normal for the current position based off of the binormal from the previous position. This ensures that between two positions the camera rolls as necessary. This gives a better feeling of actually moving along the path rather than mererly moving in a straight line. However, the movement was still extremely jerky. To prevent the view from changing quickly as the tangent changes from one position to the next, there is some filtering done. I use an alpha value and collect the previouse eye, up vector, and lookAt to compute the new eye, up vector and lookAt.
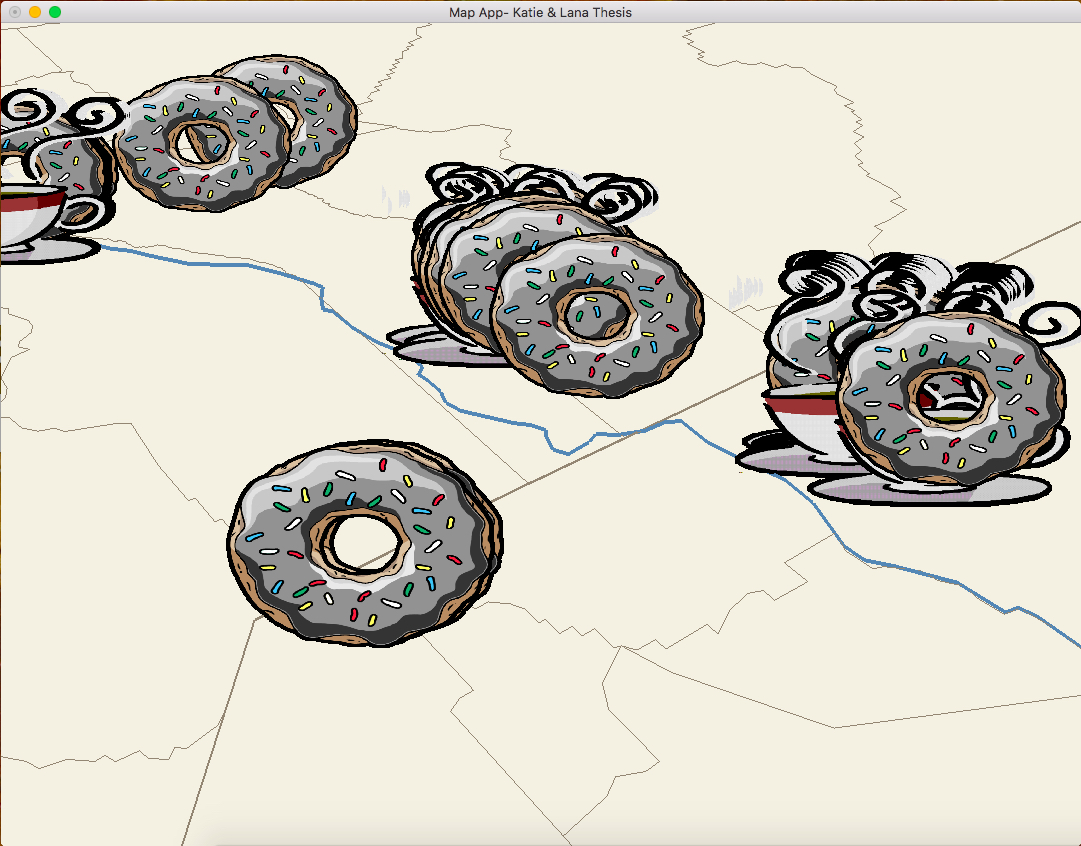Spline Camera with a target
Target Camera
The Target Camera still moves along the spline, but the lookAt is always set to a specific point. In the above image, the path goes from San Luis Obispo, CA to Boise, Idaho with a target in the middle of the path. So as the camera moves along the spline it is always pointing towards or looking back at the middle of the path. Another example is shown below along the same path but looking at San Francisco, CA.
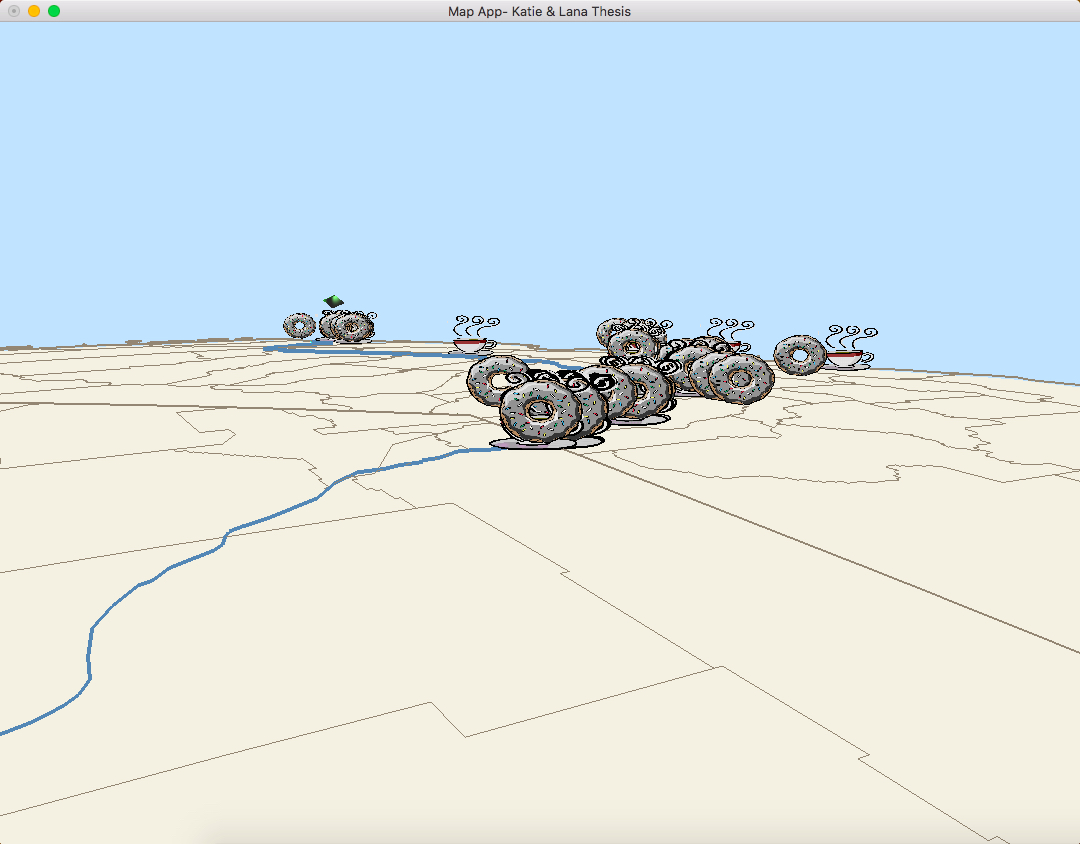Moving from San Luis Obispo, CA to Boise, Idaho always looking at San Francisco, CA.
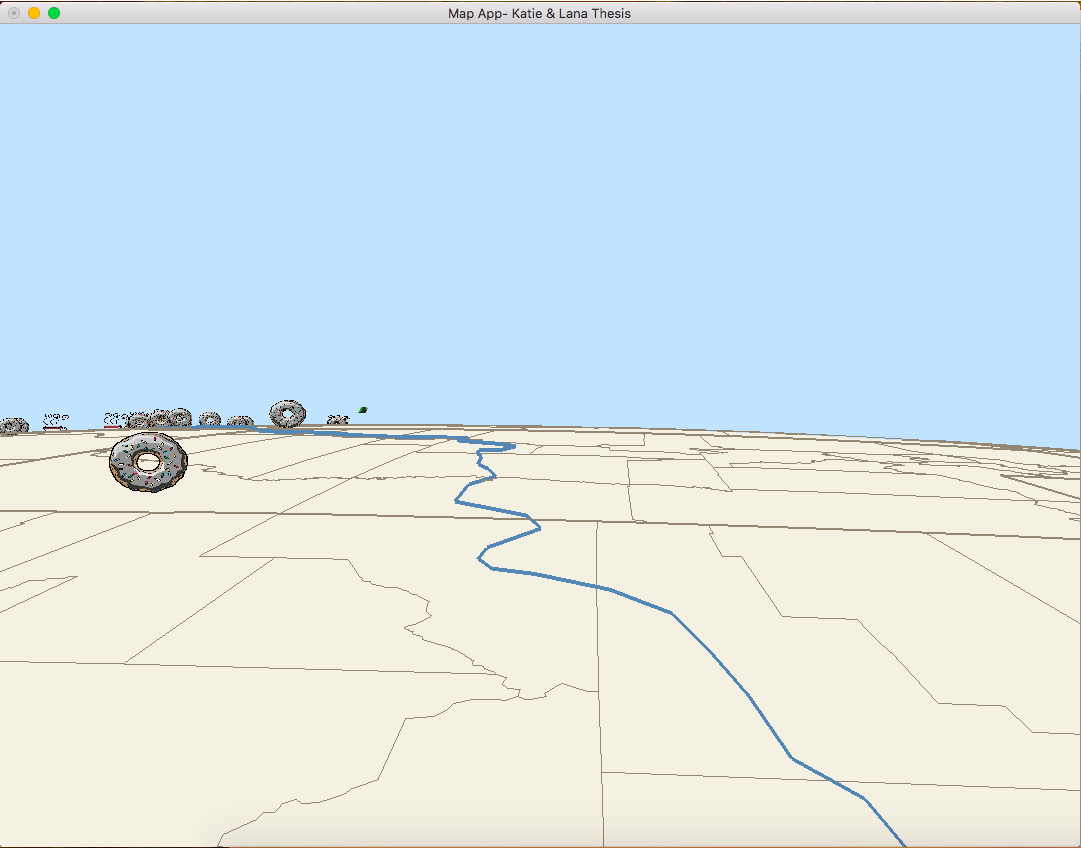Moving from San Luis Obispo, CA to Boston, MA always looking at San Francisco, CA.
Speed of the Camera
To make sure that the camera is moving at the same speed at all points along the path, arc-length parameterization is used. Along with it, I ensure that the entire path will be traversed in 45 seconds by setting the max time value to 45. I also use an ease in ease out method by setting the sNorm value to be -2 * tNorm*tNorm*tNorm + 3 * tNorm*tNorm where tNorm is std::fmod(t, tmax) / tmax and t is the current time and tmax is 45 seconds.
References
Binormal, Normal, Tangent Interpolation
Another binormal, normal, tangent interpolation method
Sprite Rendering Tutorial
Thanks for reading!
Lana Hodzic