CPE474 Final Project
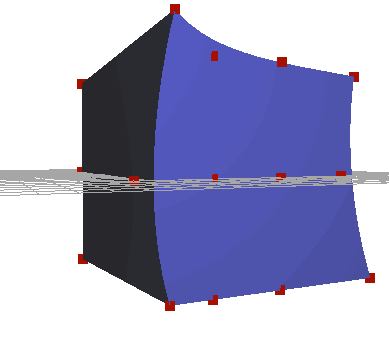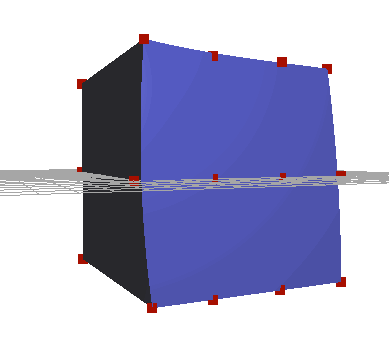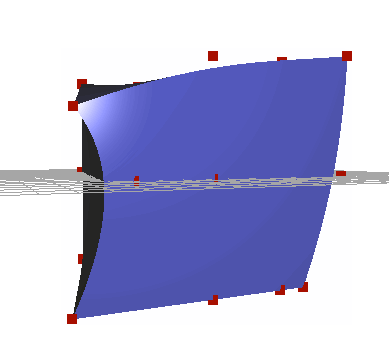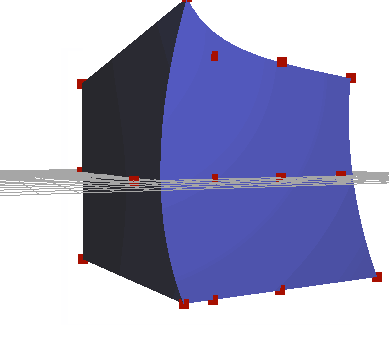
For my final project in CPE 474, I chose to focus on a basic but powerful animation technique, Freeform Deformation. I used one of the more basic implementations of Freeform Deformation outlined in Sederberg and Parry's paper on the topic[1]. My implementation uses a two step solution, where the vertices are bound to a lattice, then transformed on update.
Project Breakdown
Generating the Lattice
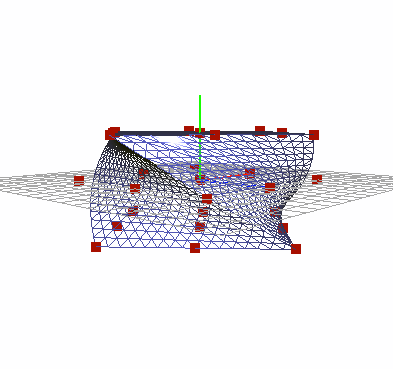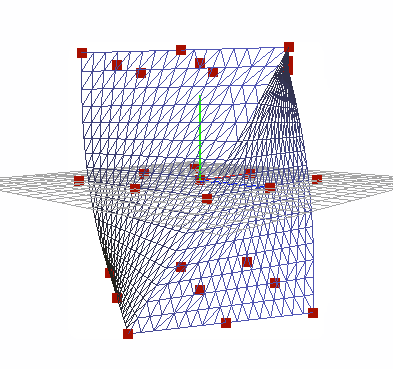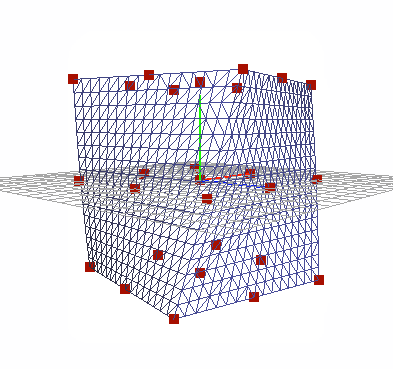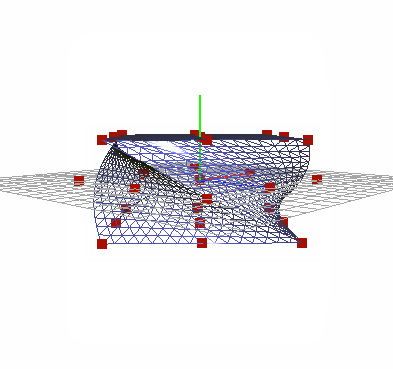
The first goal of the project was to create a lattice around a mesh. Instead of defining the lattice seperately, I wanted to auto generate it based off of the mesh bounds. After generating a series of control points, I needed to bind the current vertices to a local coordinate system. Sederberg proposes the following conversion formulae for transforming a vertex in world coordinates to a local [stu] point:
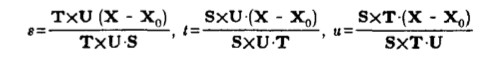
Manipulating the Lattice
Once the lattice was generated, I needed to write a flexible animation system. In the interest of time, I ended up using function pointers to deform the lattice. Animations were defined with an initial lattice size, and a function that animated the control points. For a quick demo, the animation system worked well. However, I would have liked to add additional controls, such as the ability to pick lattice points and manipulate them directly, and keyframes.
Deforming the points

In order to deform the points, I needed to evaluate the vector valued trivariante Bernstein Polynomial outlined in the paper:
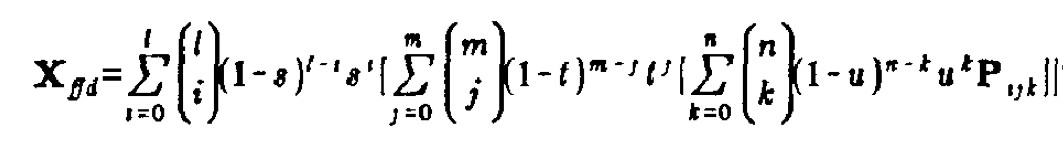
Evaluating the polynomial was initially confusing, but after further studying the equation, began to make sense. Reading right to left reveals that each block of the function returns a vector.
Further optimizations could be made by paralelizing the previous equation, or pushing the work to the shader pipeline. For my project, the algorithm is CPU bound. The largest issue with my current solution is that the normals must be regenerated each frame after deforming the points. If I were able to calcualte a matrix transformation to transform <stu> to X, a shader solution for calculating the normals would be feasable.
Any Mesh Supported

Freeform Deformation is extremely flexible due to the fact that any mesh can be wrapped by a deformation lattice. Here, the lattice is being used to animate a simple dizzy character[2]. The flexibility of FFD allows for stylized 'stretch and squish' style animations without compromising other parts of a rendering pipeline. For instance, Freeform Deformation could be inserted after vertex skinning to further animate a character.
Sources
[1]Thomas W. Sederberg and Scott R. Parry: Freeform Deformation of solid geometric models
[2] 'Cheb' humanoid model created using Cosmic Blobs software developed by Dassault Systernes Solidworks Corp.