Water Ballon Simulator

Water Balloon Simulator

By Ryan Kehlenbeck

Overall goal of the project

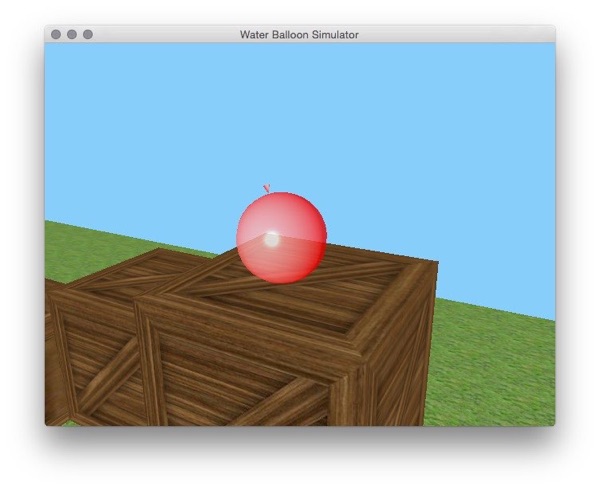
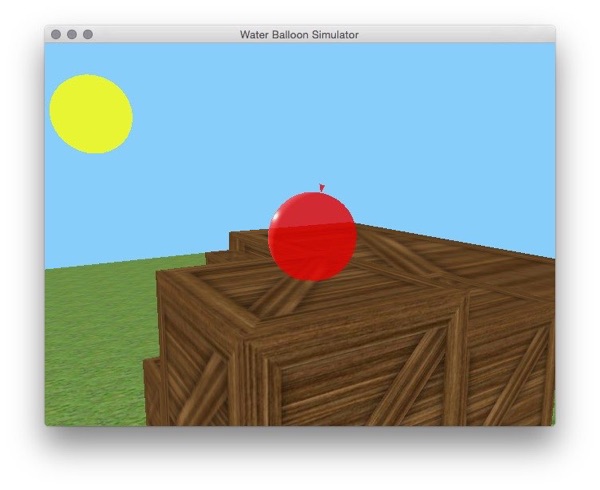
The Overall goal of the project was to create a water balloon mesh that can roll around in a 3D environment. The water balloon is procedurally generated, deformable, and collides with other objects in the world. The environment contains a ground level with a grass texture, boxes with a wooden box texture, and a “sun” that acts as a light source. The sun and balloon use Blinn-Phong shading with alpha blending so they are slightly transparent. The balloon is moved about the scene using the ‘wasd’ keys and moves with respect to the camera. The camera is a third person style camera focused on the center of the balloon that can switch between following the balloon or being locked to a certain position with the ‘f’ key.

Technical difficulties encountered

Creating the Water Balloon

The water balloon is generated using spherical coordinates. Given the center, radius, number of vertical subdivisions, and number of horizontal subdivisions, the location of each vertex in the water ballon can be found with the following formulas. The “knot” on top of the balloon is simply a circle of points connected to the north pole.

Bottom Point

South Pole = (center.x, center.y - radius, center.z)

Body

For [n = 1:horizontalSlices]

[m = 0:verticalSlices - 1]

θ = π * ((horizontalSlices + 1) - n) / (horizontalSlices + 1)

φ = 2 * π * m / verticalSlices

x = center.x + radius * sin(θ) * sin(φ)

y = center.y + radius * cos(θ)

z = center.z + radius * sin(θ) * cos(φ)

Top Point

North Pole = (center.x, center.y + radius, center.z)

Calculating Normals

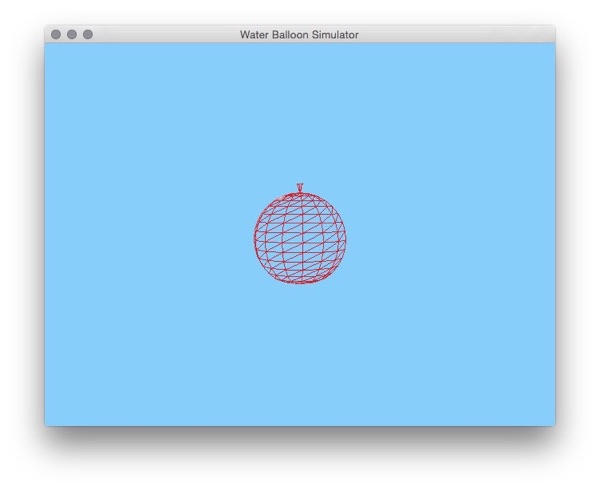
In order for the displacement of each vertex of the balloon to be visible, the normals had to be redrawn at every step. If they were not, the original normals would be used which would make the balloon always reflect light like a perfect sphere. The normal for each vertex is calculated by normalizing the sum of the normals for each adjacent face.

Face Normal

If a triangle consists of vertices a, b, and c:

v1 = b - a

v2 = c - a

face.normal = v1.cross(v2)

Vertex Normal

For each face:

a.normal += face.normal

b.normal += face.normal

c.normal += face.normal

For each vertex:

vertex.normal.normalize()

The result can be seen in the following images where the partially flattened bottom of the balloon is not lit and the fully flattened balloon reflects all of the light properly.

Physics

The water balloon maintains its shape by keeping an array of displacements for each point in relation to the center of the balloon. The center of the balloon is then moved and the points adjust themselves accordingly based on the following formulas from the paper Meshless Deformations Based On Shape Matching. The expected position g(t) for each point is calculated at each step based on the center point and α is the stiffness factor between 0 and 1.

force(t) = mass * gravity

velocity(t + h) = velocity(t) + α * (g(t) - position(t))/h + h * force(t) / m

position(t + h) = position(t) + h * velocity(t + h)

Even though these equations did move each point to its expected position, they ended up overshooting the position and the forces continued to grow. I added a random damping component to each point to create a wobble effect and gravity to make the balloon a little weighted. The formulas resulted in the following:

damping = randomFloat(-0.8, 7.5)

force(t) = mass * gravity - damping * v(t)

The values used for stiffness and gravity were 0.01 and (0, -10, 0) respectively. This resulted in the balloon wobbling to a stop instead of overshooting the expected position or stopping at exactly the expected position right away.

Collision Detection

In order to detect collisions between the boxes and the water balloon, at each step, each box takes the position of the water balloon’s center and the balloon’s radius and determines whether the point on the outside of the water balloon that is closest to the center of the box is at, or inside the bounds of the box. If the balloon is inside a box, the distance that it is inside of the box is added to the center of the balloon in the opposite direction of the collision, resulting in the balloon “bouncing” backwards.