Due to time constraints, this project went from being a potentially glorious project involving trains and multi-track drifting to a simple demonstration of Catmull-Rom splines in three dimensions.
When beginning this project the first problem I had to solve was to get objects moving along a pre-defined path. After some consultation and research I came to the conclusion that Catmull-Rom splines would the best choice because it was relatively easy to implement, relatively easy to understand, and provided curved movement.
I referenced the book, Essential Mathematics for Games and Interactive Applications, Third Edition for the theory and implementation of the Catmull-Rom spline. Most of what I understand about how the spline works is from the chapter on interpolation in the book. In short, Catmull-Rom splines are derived from Hermite curves which are a type of piecewise, continuous, parameterized cubic curve. Hermite curves were in turn a logical step up from linear interpolation between two given points; instead of using lines, you can use cubic curves (not quadratic curves due to some tangent issues I don't quite grasp).
Getting to the useful bits though, given a n number of points, a piecewise curve can be defined by the general form...
where i is the index (which curve), U is a row vector containing the variables we're interpolating, M is a matrix containing all of the coefficients for that specific curve, and G is the matrix containing the coordinates we define. Given that u is representing a percentage of the arc length of the curve, you get a point on the curve at that respective position as illustrated below
So, in implementation we can easily write a function to simply accept any number from
The specific U, M, and G matrices for Catmull-Rom splines look like this.
In the case of Catmull-Rom, the first and last points are special cases due to there not being a or a .
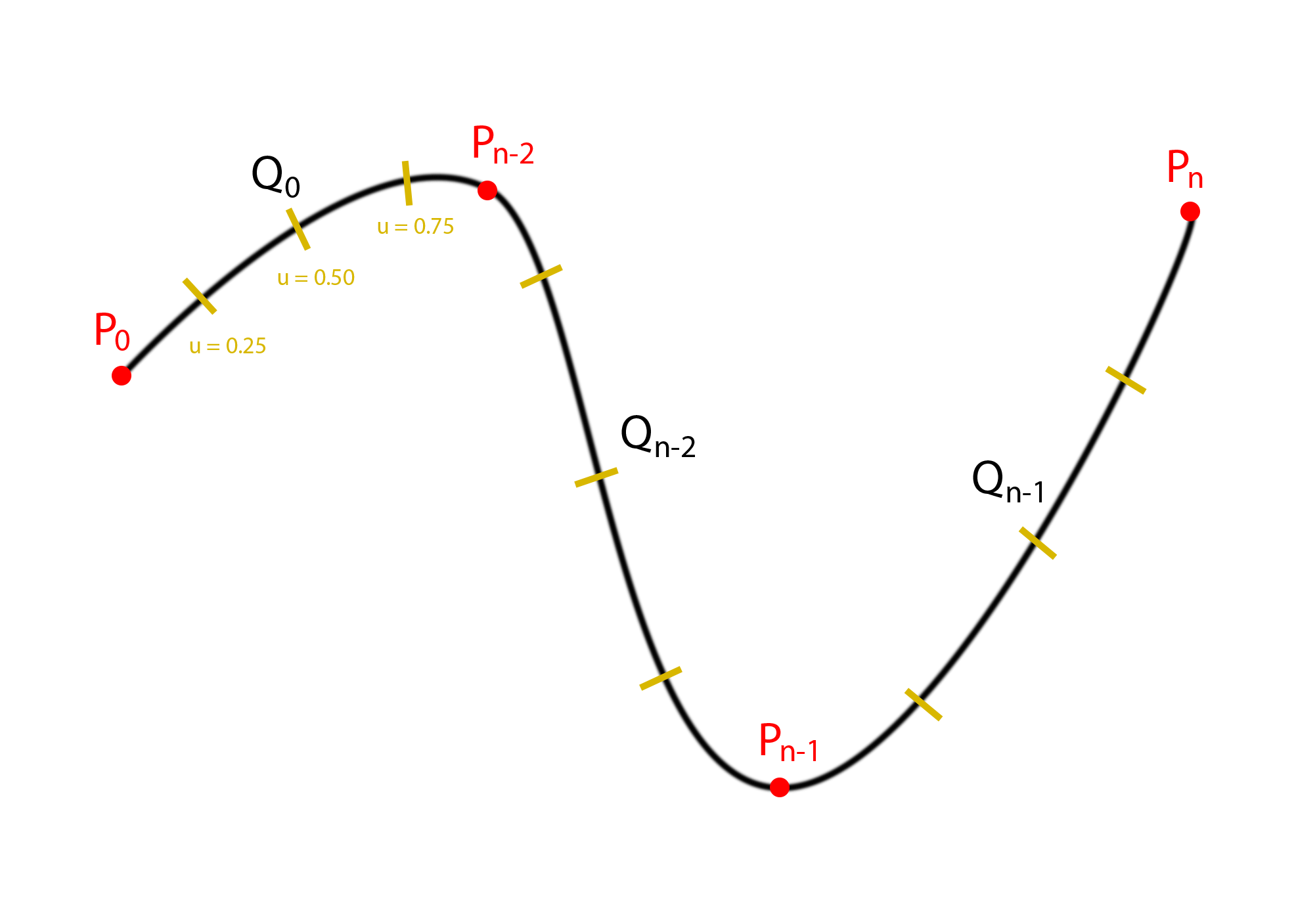
The derivation for this is detailed in the book, but in short they create two phantom points at where and are expected to be using the first two, and last two points. Also, the constant in front of the M matrix is there from the derivation and done to not to have fractional values in the matrix itself.With the above implemented, I move on to implementing constant movement along the curve. If you notice from above, due to the differing arc lengths of each curve, if you simply translated the object along the curve at a constant increment of u, you would move at different rates. The yellow lines indicate the u values at 0.25, 0.50, and 0.75 along each segment of the curve.
The solution to this problem at a high level is to answer the following question; what is the u parameter for the specific distance I want to travel? This problem requires first for us to calculate the arc length of the specific curve. Typically you would simply take the integral of the equation for the curve as that provides the most accurate solution. The issue is that this calculation is relatively expensive, so the book recommends two approximation techniques; one approximates the integral directly via an infinite series, and the other does it via line segments and linear interpolation. Due to the absurd amounts of memory my laptop has, I chose the latter. Below is an illustration of the solution.
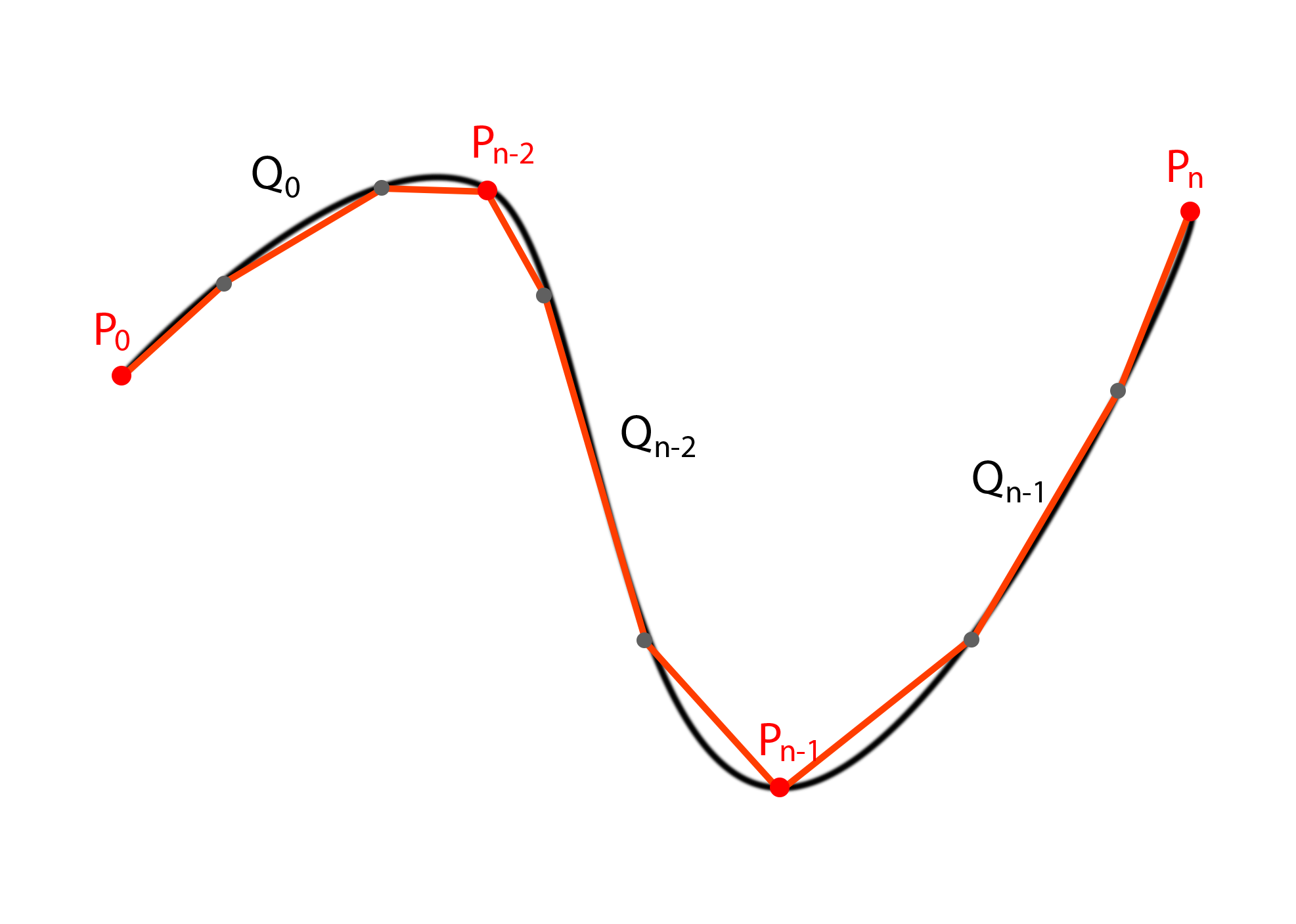
The general idea is to calculate the distance value per gray point on the curve, giving you a rough map of arc length to u value. Then, when you want to find anything inbetween you simply linearly interpolate using the two closest points with the equation below.
Where s is the approximate arc length, u is the parameter to the curve equation, and k is the index of the points in the table
With the arc length determined, the next step is to figure out how to reverse this table; you want to find the parameter per some arbitrary length. This can effectively be boiled down to solving the following.
Where is the start parameter, u is the desired parameter and s is the desired length. The optimal solution given by the book involved Newton-Raphson root finding (with a derivation using a Taylor series expansion), and bisection (which uses the mean value theorem as a basis). The idea is to combine these into a single solution for a given situation. The problem is... I barely understand the math behind it. As much as I have been taught to implement black boxes my entire coding career, a sleep deprived me could not do it. Instead I went with the second solution; you do the same thing you did to find the arc length but instead of linearly interpolating between the lengths for a given u, you linearly interpolate the u for a given length with a similar equation to above
I implemented all of the above in the project in a single class and used that to instantiate curves while needed. The graphical portions of the project are taken directly from the labs and assignments done in the class (some modified); the Blinn-Phong cel shader, the freelook camera (unchained from the ground), the plane model, the sphere model, and provided wrapper classes.
This all culiminated in an output that looks like below.
In short, I generated a huge spiraling tower comprised of spheres that move along a huge Catmull-Rom spline. The large spheres are the pre-defined the points, and the small spheres are traveling along the path.
That is unfortunately it though; my plans for train drifting and other sorts of Initial D inspired madness did not transpire in the end.
Verth, James M. Van., and Lars M. Bishop. Essential Mathematics for Games and Interactive Applications. Boca Raton: CRC/Taylor & Francis Group, 2016. Print.