CSCE 441: Computer Graphics

Fall 2017

Assignment 3: Fractals and Iterated Function Systems [150 points]

Due 10/11/2017

Purpose:
The purpose of this assignment is to help you become familiar with 2D transformations and to use these transformations to construct fractals through Iterated Affine Transformations.

Description:
In this assignment you will create a program that can display attractors created by Iterated Affine Transformations. Since these attractors are created through transformations, you will implement functions that create matrices representing each transformation. You may NOT use any of OpenGL's transformation functions or matrix functions for this assignment. In order to test your code, we have developed a skeleton application for you to modify when creating your program. The code defines the functions you must implement for this assignment. Later, we will replace the init.cpp file with our own to test your code on new fractals you have not seen before. You may build your own data structures/functions on top of this code and are not restricted to only these functions. However, do not modify the given function definitions/types so that our test code will compile with your program.

The functions you must implement are:
  • translate(vector): constructs a matrix that translates by the given vector
  • rotate(point, angle): constructs a matrix that rotates about the given point by the specified angle (in radians)
  • scale(point, amount): constructs a matrix that uniformly scales about the given point by the amount specified
  • nscale(point, vector, amount): constructs a matrix that non-uniformly scales about the given point in the direction of a unit length vector by the amount specified
  • image(p1,p2,p3, q1,q2,q3): constructs a matrix that maps the points p1,p2,p3 into q1,q2,q3
  • compose(m1, m2): returns the multiplication of the matrices m1*m2 (in that order)
  • setCondensationSet(list of points): sets the current condensation set. If the list is empty, then no condensation set should be used. If there is only one point in the list, the condensation set is a point. If there is two points in the list, the condensation set is a line. If there are more than two points, the condensation set is a poly-line (line connecting all points and the first/last point).
  • setIATTransformations (list of matrices): sets the list of matrices to be used as the current IAT
  • display: draws the current IAT on the screen
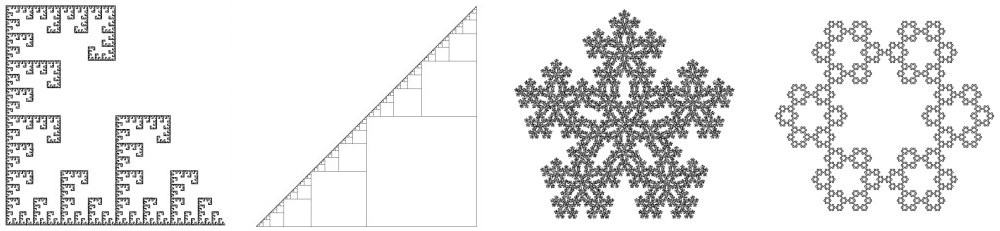
Initially your program should display the attractor of the IAT specified in init.cpp (if no IAT is specified, your program can start off displaying nothing). When the user presses keys 1-6, you should set the current IAT to a set of transformations that display the following fractals:
  • "1": Fractal Hangman
  • "2": Fractal Staircase
  • "3": Fractal Snowflake
  • "4": Hex Flower
  • "5": Your own fractal #1
  • "6": Your own fractal #2
Here are pictures of the first four fractals in order.

You should also create two of your own fractals (points will be given for creativity) and display them if the user presses "5" or "6".

Finally, we strongly suggest you make sure your program compiles in VS.NET since we will be compiling your programs to test their behavior on unknown fractals. Do not place addition functions inside of init.cpp because we will overwrite that file with our own. Do not change the reshape function either. The window will have coordinates (-1,-1) to (1,1).

Grading:
[5] Correct behavior when user presses number keys
[5] Implementation of translate
[5] Implementation of rotate
[5] Implementation of scale
[5] Implementation of nscale
[5] Implementation of image
[5] Implementation of compose
[5] Implementation of setCondensationSet
[5] Implementation of setIATTransformations
[5] Correct algorithm for displaying the attractor
[10] Fractal Hangman
[10] Fractal Staircase
[10] Fractal Snowflake
[10] Hex Flower
[15] Creativity/Originality of own fractal #1
[15] Creativity/Originality of own fractal #2
[30] Correct behavior on unknown fractals