Large Integer Arithmetic
An integer in C is typically 32 bits, of which 31 can be used for
positive integer arithmetic. This is good for representing numbers
up to about two billion (2 times 109).
Some compilers, such as GCC,
offer a "long long" type, giving 64 bits capable of representing
about 9 quintillion (9 times 1018)
This is good for most purposes,
but some applications require many more digits than this. For example,
public-key encryption with the RSA algorithm typically requires 300
digit numbers. Computing the probabilities of certain real events
often involves very large numbers; although the result might fit in
a typical C type, the intermediate computations require very large numbers.
For example, what is the probability of winning the Texas Lottery jackpot
prize with one ticket? The number of combinations of 50 numbers taken
6 at a time, "50 choose 6", is 50!/((50-6)!6!). That number is
15,890,700, so the odds of winning are 1/15,890,700. The number 15,890,700
can be represented easily by a C integer, but the (naive) computation
of that number involves computing 50!, which is:
30,414,093,201,713,378,043,612,608,166,064,768,844,377,641,568,960,512,000,000,000,000
This number will not fit into a C integer, not even a 64 bit one.
So we must move to a different representation of non-negative integers.
We can represent a number as a sequence of digits stored in an array
of integers.
We can write functions to add, multiply, etc. on those arrays, and then
make them as large as we want.
In our new representation, we have an array of "digits" (integers) in
some base b. Typically, b = 10, our normal decimal
number system; that makes things easy to print. The 0'th array element
is the 1's place, the #1 element is the ten's place, the #2 element is
the hundred's place, and so forth (really, the b0's
place, the b1 place, the b2 place,
etc.)
Let's look at some algorithms doing arithmetic on our new "big" integers.
We'll let N be the number of digits we will represent. If we
need any more, we just increase N. Let BASE be the
base of our number system, understood to be 10 typically, but can be
changed if we like.
First, we need a way of making a "normal" integer into a "big" integer;
we'd like a function called make_int such that e.g.
make_int (A, 123) would put 3 in A[0], 2 in A[1],
1 in A[2], and zeros in A[3..N-1]. We'll
do these in C rather than pseudocode because the code works out very
easily:
/* put the normal int n into the big int A */
void make_int (int A[], int n) {
int i;
/* start indexing at the 0's place */
i = 0;
/* while there is still something left to the number
* we're encoding... */
while (n) {
/* put the least significant digit of n into A[i] */
A[i++] = n % BASE;
/* get rid of the least significant digit,
* i.e., shift right once
*/
n /= BASE;
}
/* fill the rest of the array up with zeros */
while (i < N) A[i++] = 0;
}
This algorithm takes  (N)
time and space.
(N)
time and space.
Now let's look at an algorithm to add one to a big integer. This is a
common operation and easier than full addition, so we'll look at it first:
/* A++ */
void increment (int A[]) {
int i;
/* start indexing at the least significant digit */
i = 0;
while (i < N) {
/* increment the digit */
A[i]++;
/* if it overflows (i.e., it was 9, now it's 10, too
* big to be a digit) then...
*/
if (A[i] == BASE) {
/* make it zero and index to the next
* significant digit
*/
A[i] = 0;
i++;
} else
/* otherwise, we are done */
break;
}
}
This algorithm takes O(N) time in the worst case
(imagine 9999999999...) and 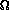 (1)
in the best case (no overflow in the least significant digit).
(1)
in the best case (no overflow in the least significant digit).
Now let's look at the more general case of addition of two big integers.
Here, we want to add two big ints in arrays called A[0..N-1]
and B[0..N-1], and put the result into C[0..N-1].
We'll use the algorithm we learned in grade school: add corresponding digits,
plus a "carry" generated by previous overflows.
/* C = A + B */
void add (int A[], int B[], int C[]) {
int i, carry, sum;
/* no carry yet */
carry = 0;
/* go from least to most significant digit */
for (i=0; i<N; i++) {
/* the i'th digit of C is the sum of the
* i'th digits of A and B, plus any carry
*/
sum = A[i] + B[i] + carry;
/* if the sum exceeds the base, then we have a carry. */
if (sum >= BASE) {
carry = 1;
/* make sum fit in a digit (same as sum %= BASE) */
sum -= BASE;
} else
/* otherwise no carry */
carry = 0;
/* put the result in the sum */
C[i] = sum;
}
/* if we get to the end and still have a carry, we don't have
* anywhere to put it, so panic!
*/
if (carry) printf ("overflow in addition!\n");
}
This function does constant work in a loop that iterates N
times, so the time for addition is  (N).
(N).
Multiplication is next. Recall from grade school how you multiplied
two large numbers A and B: starting with
the least significant digit, you multiplied each digit of A
with every digit of B, forming a partial product. You shifted
this product over to the left for each new digit, writing overflowed
digits above A to remind yourself to add them in.
We will need a function multiply_one_digit that will
multiply an entire big integer by a single digit, placing the result in
a new big int. We also need a function shift_left that shift
a number over to the left a number of spaces, effectively multiplying
it by BASEi where i is the number of spaces.
Here is the algorithm to multiply:
/* C = A * B */
void multiply (int A[], int B[], int C[]) {
int i, j, P[N];
/* C will accumulate the sum of partial products. It's initially 0. */
make_int (C, 0);
/* for each digit in A... */
for (i=0; i<N; i++) {
/* multiply B by digit A[i] */
multiply_one_digit (B, P, A[i]);
/* shift the partial product left i bytes */
shift_left (P, i);
/* add result to the running sum */
add (C, P, C);
}
}
Now let's look at the function that multiplies by
a single digit:
/* B = n * A */
void multiply_one_digit (int A[], int B[], int n) {
int i, carry;
/* no extra overflow to add yet */
carry = 0;
/* for each digit, starting with least significant... */
for (i=0; i<N; i++) {
/* multiply the digit by n, putting the result in B */
B[i] = n * A[i];
/* add in any overflow from the last digit */
B[i] += carry;
/* if this product is too big to fit in a digit... */
if (B[i] >= BASE) {
/* handle the overflow */
carry = B[i] / BASE;
B[i] %= BASE;
} else
/* no overflow */
carry = 0;
}
if (carry) printf ("overflow in multiplication!\n");
}
And finally the function to shift left a certain number of spaces:
/* "multiplies" a number by BASEn */
void shift_left (int A[], int n) {
int i;
/* going from left to right, move everything over to the
* left n spaces
*/
for (i=N-1; i>=n; i--) A[i] = A[i-n];
/* fill the last n digits with zeros */
while (i >= 0) A[i--] = 0;
}
The shift_left and multiply_one_digit algorithms
each do a constant amount of work in a loop that runs for
 (N) time, so they each
take time
(N) time, so they each
take time  (N).
Addition also takes
(N).
Addition also takes  (N)
time; all three are done in the multiply function a constant
number of times within a loop that iterates N times, so
multiply takes a time in
(N)
time; all three are done in the multiply function a constant
number of times within a loop that iterates N times, so
multiply takes a time in
 (N2).
(N2).
Some comments on large number arithmetic:
- It turns out that, using a divide and conquer algorithm, one can obtain
an algorithm that works in time
 (Nlg 3)
= O(N1.59), much better than the
quadratic time above. However, this technique only becomes efficient for
very large values of N. There is another technique using the
Fast Fourier Transform that multiples numbers in
O(N log N log log N)
time, which is even better, but still only becomes efficient for large
values of N (e.g. > 10,000 decimal digits).
(Nlg 3)
= O(N1.59), much better than the
quadratic time above. However, this technique only becomes efficient for
very large values of N. There is another technique using the
Fast Fourier Transform that multiples numbers in
O(N log N log log N)
time, which is even better, but still only becomes efficient for large
values of N (e.g. > 10,000 decimal digits).
-
A practical way to get more out of this algorithm is to increase BASE;
this way, the same number of bits can be represented with less storage
(i.e., lower value of N). The reason for choosing 10, other
than the fact that it makes doing examples easy, is that it makes
printing the numbers out a matter of traversing the array; other bases
require complex conversions of bases.
If we keep BASE as a power of 10 (e.g. 10,000), we can still easily
print the numbers (fixing up leading zeros when we find them), and still improve
performance.
- If we let BASE=2, then we are doing binary arithmetic.
Multiplying by a single digit then becomes trivial: the partial product
of n * A[0..N-1]
is either all zeros (if the n=0) or A[0..N-1]
itself (if n=1). This fact is not lost on computer architects,
who implement multiplication algorithms in binary all the time :-)
- These are some simple arithmetic algorithms. There are other algorithms
for integer division, subtraction (requiring a representation of negative
numbers), exponentiation, modulus, etc. that are somewhat more complex but
are basically the same idea. When we look at RSA encryption, we will
assume a full implementation of large number arithmetic, being careful to
take into account the various asymptotic complexities.
- If you would like to play with very large numbers, the Unix command
bc implements "arbitrary" precision arithmetic; type bc
at the command prompt and then type something ridiculously large like
2^1000 (2 to the 1000 power). The result will quickly come back.
 (Nlg 3)
= O(N1.59), much better than the
quadratic time above. However, this technique only becomes efficient for
very large values of N. There is another technique using the
Fast Fourier Transform that multiples numbers in
O(N log N log log N)
time, which is even better, but still only becomes efficient for large
values of N (e.g. > 10,000 decimal digits).
(Nlg 3)
= O(N1.59), much better than the
quadratic time above. However, this technique only becomes efficient for
very large values of N. There is another technique using the
Fast Fourier Transform that multiples numbers in
O(N log N log log N)
time, which is even better, but still only becomes efficient for large
values of N (e.g. > 10,000 decimal digits).
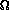 (1)
in the best case (no overflow in the least significant digit).
(1)
in the best case (no overflow in the least significant digit).