Read this question paper carefully. Write your answers in the bluebooks
provided. Make sure to write your name on your bluebook. Do not write
anything you want graded on the question paper. If you need another bluebook
or if you have a question, please come to the front of the classroom.
You may keep this question paper when you leave.
- Draw the circuit diagram for an AND gate using PMOS and NMOS
transistors. Use at most 6 transistors. Hint: like the other logic gates
we have seen, some transistors will be wired in series and some will be
wired in parallel.
Solution (12 points): (click to enlarge)
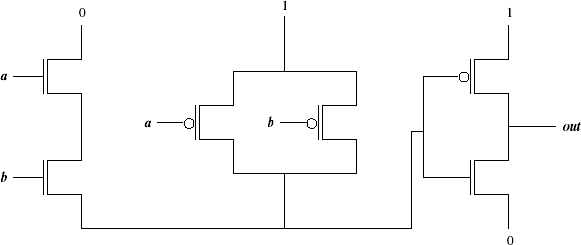
The leftmost four transistors form a NAND gate. The two on the right
form a NOT gate. Note that NAND is 0 if and only if both a and b are 1.
Thus the two n-type transistors at the left of the diagram allow a 0 to
flow to the input of the NOT gate only when both a and b trigger the gate
inputs of their respective n-type transistors. NAND is 1 if either of a or
b, or both, are 0. Thus, the two p-type transistors in the middle of the
diagram allow a 1 to flow to the input of the NOT gate if either a or b or
both are 0, triggering the gate input of one or both p-type transistors.
The NOT gate accepts the output of the NAND gate. If it is 0, then the
p-type transistor is triggered and a 1 flows to the output. If it is 1,
then the n-type transistor is triggered and a 0 flows to the output.
- Consider the following x86 assembly language subroutine:
compute:
pushl %ebp
movl %esp,%ebp
subl $8,%esp
andl $0xfffffff0,%esp
movl $0,%ecx
movl $1,%edx
movl $3,%eax
loop:
addl %edx,%ecx
addl %ecx,%edx
decl %eax
jns loop
pushl %edx
pushl $.L1
call printf
leal 8(%esp),%esp
xorl %eax,%eax
leave
ret
.L1: .string "%d\n"
This subroutine is similar to the one you decoded in your first homework.
It is in the GNU assembler syntax, so the 'l' in e.g. xorl means
"32-bit longword" and the destination of an instruction is in the last place,
e.g. "addl %edx,%ecx" adds the contents of the two registers and
places the result in %ecx.
- Suppose this subroutine is called from main. What will be
the output of this program?
Solution (1 point):
34
Recognize that this code is very similar to the string of bytes you decoded
in the first homework. It computes the first several Fibonacci numbers
by adding %edx to %ecx, and adding %ecx to %edx, where %ecx and %edx are
initially 0 and 1, respectively. The value of %edx is printed. The body of
the loop beginning with "loop:" and ending with "jns" is executed 4 times,
with the values of %eax, %ecx, and %edx being the following at the end of
each iteration of the loop:
Iteration # %eax %ecx %edx
1 2 1 2
2 1 3 5
3 0 8 13
4 -1 21 34
When %eax is decremented to -1, the sign bit is set and the "jns" instruction
("jump if not sign") will fall through. Then printf is called with %edx
as the parameter to print in the "%d" format.
- How many instructions will this subroutine execute (not including
instructions in the implementation of printf)?
Solution (2 points):
7 instructions before the loop
+ 4 * 4 instructions in the loop
+ 7 instructions after the loop
= 30 instructions.
- Suppose we add a main subroutine that calls compute
like this:
main:
pushl %ebx
movl $100,%ebx
loop2:
call compute
subl $1,%ebx
jnz loop2
popl %ebx
ret
This code simply calls compute 100 times. Suppose we are using
a Smith (i.e. bimodal) branch predictor with 2-bit saturating counters.
How many times will the jns instruction in compute
be predicted incorrectly? Assume that all counters are initially 0, and
there are enough counters so that other branches do not interfere with
the prediction of jns.
Solution (2 points):
Recall that a Smith predictor uses the branch address to index a table of
counters. The high bit of the counter is used as the prediction, and the
counter is incremented when the branch is taken, decremented otherwise,
saturating at 0 and 3. So the branch will be predicted taken when the
counter is 2 or 3, and not taken when the counter is 0 or 1. The loop
iterates 4 times each time "compute" is called, so the "jns" branch has a
pattern of "taken, taken, taken, not taken." There is only one counter
to be concerned about: the counter to which the address of "jns" maps.
The counter is initially 0, so the first iteration of the loop will look
like this:
counter before prediction actual outcome correct counter after
0 not taken taken no 1
1 not taken taken no 2
2 taken taken yes 3
3 taken not taken no 2
So the first iteration incurs 3 incorrect predictions. The next iteration
will look like this:
counter before prediction actual outcome correct counter after
2 taken taken yes 3
3 taken taken yes 3
3 taken taken yes 3
3 taken not taken no 2
So the second iteration incurs 1 incorrect prediction. Note that the
counter has the value 2 both when the loop is entered and after the last
iteration of the loop is completed, so the behavior of the predictor will
repeat this same pattern for each subsequent iteration. The loop executes
1 iteration with the first pattern and 99 iterations with the second pattern.
So the total number of incorrect predictions is: 1 * 3 + 99 * 1 = 102.
- Suppose that these instructions are executed on a computer with a
classic 5-stage pipeline. This microprocessor has only one functional
unit for adding. Using the four instructions following the line labeled
loop, give one example of each of the 3 types of pipelining hazards.
For each example, suggest a modification to the microarchitecture that
would mitigate the hazard. Make sure to specifically state how that
modification would help in each case.
Solution (3 points, 1 for each hazard):
1. Structural hazard. The combination of "decl" followed by "jns"
involves contention for the adder. The "jns" instruction is in the ID
stage and needs to compute its target address using the adder while the
"decl" instruction is in the EX stage and needs the adder to decrease
%eax by 1. (The same cannot be said about the two "addl" instructions;
the adder works in the EX stage and only one instruction can be in the
EX stage at the same time.) Supplying an additional adder for computing
branch offsets would eliminate this problem.
2. Control hazard. The "jns" instruction might be followed by the first
"addl" instruction if the branch is taken. When the "jns" instruction is
in the ID stage, the subsequent instruction should be in the IF stage,
but it is not clear until the EX stage or possibly the WB stage which
instruction that should be. Branch prediction would mitigate this problem.
Branch delay slots would mitigate this problem.
3. Data hazard. There are at least two potential Read After Write (RAW)
hazards. This type of hazard would be caused by a data dependence between
two instructions that are so close that the data producer hasn't reached
the WB stage by the time the data consumer reaches the ID stage. Examples:
- The pair of "addl" instructions in the loop. The second reads
%ecx after the first write %ecx. The first is only in the EX
stage when the second is in the ID stage trying to read %ecx.
- The "decl" followed by "jns" ending the loop. The "jns"
instruction tries to read the value of the SF condition code
produced by the "decl" instruction, causing a RAW hazard since
the instructions proceed through the pipeline in adjacent stages.
(This is not a control hazard, but it can exacerbate the control
hazard mentioned above by increasing the number of stall cycles
needed before the next instruction can be fetched.)
Forwarding can mitigate this hazard and dynamic scheduling can keep it from
stalling the entire pipeline and allowing independent instructions to execute
while the data hazard is being resolved. (Actually, value prediction could
mitigate the data hazard itself, but we haven't talked about that in class.)
- Suppose that these instructions are executed on a statically scheduled
superscalar machine with unlimited functional units. This machine
can execute up to 4 instructions per cycle. Give examples from the
compute subroutine of 4 consecutive instructions that may all
execute in the same cycle.
Solution (2 points):
The test says "examples" plural without specifying how many, so 2 examples
would suffice. However, there seems to be only 1 example:
- The sequence of 4 instructions beginning with "andl" are mutually
independent, neither reading nor writing the same data. They can
all be executed in the same cycle.
Some examples come close:
- The 4 instructions beginning with "leal" seem independent, but
each of the "leal," "leave," and "ret" instructions read and write
%esp, so they cannot be completely executed in parallel.
- The 4 instructions beginning with "jns" seem independent, but
again the two "pushl" instructions and the "call" instruction read
and write %esp so they cannot be executed in parallel.
- Suppose that these instructions are executed on a dynamically scheduled
superscalar machine with unlimited functional units executing up to 4
instructions per cycle. Give two examples of a pair of instructions that
can be executed out of order. Give two examples of a pair of instructions
that cannot be executed out of order.
Solution (2 points):
Any pair of instructions that are not separated by control-flow instructions
could be issued out-of-order on a dynamically scheduled superscalar.
However, they often cannot be executed out of order if there are data
dependences between them.
Examples of instructions that can be executed out of order:
- "movl $0,%ecx" and "movl $1,%edx." They are indepdendent.
- "movl $1,%edx" and "movl $3,%eax." They are indepdendent.
- "movl $0,%ecx" and "movl $3,%eax." They are indepdendent.
- "leal / xorl." They are independent.
- Either of the two "addl" instructions in the loop and the "decl"
instruction in the loop. They are independent.
Examples of instructions that cannot be executed out of order:
- "pushl %ebp" and "movl %esp,%ebp." The "pushl" instruction writes
the %esp register, and the new value of %esp is read by the "movl."
- The two "addl" instructions in the loop. There is a RAW hazard.
In general, instructions that are separated by a control-flow instruction
such as the "jns" or possibly the "call" could not be executed out of order.
In the case of "jns," for example, the "pushl %edx" instruction could not
be executed before the "jns" had been executed. Some instructions with
data dependences cannot be executed out of order, e.g. the two "addl"
instructions in the loop. In the case of "call," we can safely assume
that the code to execute the printf function will contain at least one
conditional branch.
- When we are designing a new ISA, having a lot of registers seems like
a good idea. However, what are at least two disadvantages of having a
large number of registers in the ISA?
Solution (12 points):
Here are some disadvantages:
1. A larger register file takes longer to access, and might increase the
clock period for the microarchitecture.
2. Increasing the number of registers increases the number of bits needed
to represent a register in an instruction. This will cause problems
representing instructions in a fixed-length word, or might necessitate
moving to a larger instruction word.
3. On a context switch, all registers must be saved. With more registers,
the overhead of saving them is higher.
There were some weaker answers that were also accepted. Chief among these
were "increasing chip complexity" and "more registers are more expensive (in
terms of area or energy or whatever)." You could say this about almost any
new feature added to an ISA; that's why these answers are weaker. (However,
no points were taken off for correct but weak answers. Points were taken
for weak and incorrect answers.)
- Consider a 64KB 4-way set associative cache. The cache has blocks of
64 bytes, and there are 1 valid bit and 1 dirty bit per block. A physical
address has 46 bits. How many total SRAM bits will be needed to implement
this cache? Show your work.
Solution (12 points):
There are 64K bytes. 64K is 216. 64 is 26. 4 is 22.
There are 216 / 26 = 210 total blocks.
There are 210 / 22 = 28 sets.
So a physical address can be broken down into the following fields:
[ 32 bits of tag | 8 bits of set index | 6 bits of block offset ]
32 + 8 + 6 = 46 so all address bits are accounted for.
Each of the 210 blocks needs 32 = 25 bits of tag.
In addition, a block needs 1 valid bit + 1 dirty bit = 2 extra bits.
So the meta-data for the entire cache is:
25 * 210 + 2 * 210 = 32 * 1024 + 2 * 1024 = 32768 + 2048 = 34816 bits.
Each block consists of 64 bytes, or 64 * 8 = 26 * 23 = 29 bits.
So the data for the cache is 210 * 29 = 219 = 524288 bits.
So the whole cache needs 524288 + 34816 = 559104 bits of SRAM.
- It has been observed that a small direct-mapped instruction cache
can have fewer misses than a fully associative instruction cache using
an LRU replacement policy, even though both caches have the same number
of blocks and the same number of bytes per block. What program behavior
can elicit such a counterintuitive result? Why?
Solution (12 points):
This was one of the questions from the review. The solution is to notice
that the pattern of instruction accesses in loops is at odds with the LRU
replacement policy. Suppose the fully associative cache has n blocks,
and there is a loop that contains n+1 blocks. When the loop reaches the
branch that brings it back to the beginning, the next access will go to the
least recently used block in the loop, i.e., the first block. In a fully
associative cache, this block will have been replaced to make room for
one of the other n+1 blocks in the loop. This will incur a cache miss,
causing replacement of some other block. That block will be the least
recently used block, i.e., the next block in the loop. However, the next
access will be to that block, causing another cache miss: we just had that
block in the cache and we threw it out, only to bring it right back in.
Clearly this pattern of access will have a cascading effect and every
single access in the loop will cause a cache miss. Contrast this with a
direct-mapped cache: there will be 1 or possibly 2 conflict misses in the
loop, but every other access to a block in the loop will hit in the cache.
- The quantum, i.e., the maximum amount of time between context switches,
has remained more or less the same for the last couple of decades. However,
the number of instructions executed per second has increased steadily.
What impact does this have on data cache hit rates? Why?
Solution (12 points):
Being able to execute more instructions in a quantum of time generally leads
to higher data cache hit rates. After a context switch, a process has a
large part of its working set flushed from the cache by other processes.
When the process begins to run again, it spends a certain number of
instructions causing cache misses and refilling the cache with its
working set, and the rest of the time with relatively fewer cache misses.
When there are more instructions executed per quantum, this first phase
involves relatively fewer instructions and the second phase involves
relatively more, so more time is spent in a phase during which the hit
rate is relatively higher.
The effect is the same as if we held the number of instructions executed
per second constant, but decreased the quantum. Each process would be
interrupted more often and do less useful work and cause more cache misses.
- In the Patterson and Ditzel paper, several advantages were listed of
RISC over CISC. Describe three of these advantages.
Solution (12 points):
- Implementation feasibility: being able to fit an entire CPU on a single
chip.
- Design time. A chip that takes less time to design can take more advantage
of advances in VLSI than a chip that takes longer.
- Speed. By reducing the complexity of the CPU, various critical paths
in circuits will be shorter so the clock period can be shorter.
- Better use of chip area. A RISC is implemented with fewer transistors
than a CISC. Given the same chip area, the RISC could devote more area
to an on-chip cache, improving performance.
- Better mapping of high-level languages to machine language. CISC
instructions that are intended to support some high-level language concept
often end up unused because the concept is implemented differently for
different languages and/or the compiler cannot analyze the code well enough
to apply the concept. RISC avoids this by providing simpler instructions
that are easier to compile for.
- Answer the following questions briefly, i.e., with just a few words or
a single sentence:
- In a processor that performs speculative execution, what is the name
of the structure that supports precise interrupts and holds speculative
results of instructions before they commit?
Solution (2 points): Reorder Buffer
- What is temporal locality?
Solution (2 points): The tendency of accesses to be clustered in time.
- What is spatial locality?
Solution (2 points): The tendency of accesses to be clustered in space.
- Branch instructions usually represent their destination addresses
as an offset from the current program counter, thus the destination of a
branch is only known after this sum has been computed. What is the name
of the structure that caches these computations to speed up branching?
Solution (2 points): Branch Target Buffer
- In general, which has better locality, code or data?
Solution (2 points): Code
- What is a victim cache?
Solution (2 points): A buffer that holds recently evicted cache blocks
that can be accessed in parallel with the cache.
- What is the middle name of your professor for 505?
Solution (2 points): Ángel (this "secret" was given to the few
students who showed up on time one day when initial attendance was
particularly low).
Average score: 75.67
