Lecture 7: Caches

Memory Hierarchy

Computer systems often need a large amount of storage to accomplish their goals. There are many different kinds of storage devices. As a rule, faster storage devices cost more per byte of storage. Thus, multiple levels of storage are used. Ideally, the resulting memory hierarchy costs only a little more than using only the least expensive memory, but delivers performance almost equal to using only the most expensive memory.

Memory Hierarchy
Type of Memory	Typical Size	Speed	Cost	Typical Organization	Technology
CPU Registers	128 bytes	1 cycle	Very high	Explicitly managed	High-speed latches
Level 1 D-Cache	8KB to 64KB	1 to 3 cycles	High	2-way set associative, 64 byte lines	6T or 8T SRAM
Level 1 I-Cache	8KB to 64KB	1 cycle	High	2-way set associative, 64 byte lines	6T or 8T SRAM
Level 2 Unified Cache	128KB to 2MB	6 to 20 cycles	Moderate	2-way set associative, 64 byte lines	6T SRAM
Main memory	4MB to a few GB	~100 cycles	Low, ~$.1/MB	Banks and Buffers	SDRAM
Disk	Hundreds of GB	~5,000,000 cycles	Very Low, ~$1/GB	Swap partition	Rotating platters

Caches

We will focus on the L1 and L2 caches in the memory hierarchy, although much of the discussion can apply to any level. For now, let us imagine that there is only one cache between the CPU and main memory. The basic idea is to have a small, expensive cache memory hold frequently used values from the larger, cheap main memory. This way, access to data and instructions is significantly faster than it would be with just the main memory. When an access to memory is available from the cache, it is said that a cache hit has occurred. When an access is not in the cache, a cache miss occurs. For a given cache access latency, we want to minimize the miss rate, i.e., the fraction of accesses to memory that miss in the cache.

Why do caches work?

The answer to this question is locality of references. The distribution of data and instruction accesses to memory is highly non-uniform. Although a program may touch many memory locations, most accesses tend to focus on just a few memory locations. If we cache these locations, we can make the average access a lot faster without having to have a large cache. There are two kinds of locality that are important for caches:

Temporal locality. This is the observation that if memory location i is accessed now, then memory location i is likely to be accessed again in the near future.
Spatial locality. This is the observation that if memory location i is accessed now, then memory locations near i are likely to be touched again in the near future.

Programs that don't exhibit a lot of locality tend not to perform well on modern processors because they can't take advantage of the cache. It's important for programmers interested in performance to be aware of locality and, if possible, write their programs to take advantage of the cache. For example, consider the following C function to multiply two matrices:

void matrix_multiply (float A[N][K], float B[K][M], float C[N][M]) {
        int     i, j, l;

        for (i=0; i<M; i++) for (j=0; j<N; j++) {
                C[i][j] = 0.0;
                for (l=0; l<K; l++)
                        C[i][j] += A[i][l] * B[l][j];

        }
}

Two dimensional arrays in C are laid out in row-major order. This means that it is laid out row by row, so that e.g. element C[0][0] is adjacent to C[0][1] in memory. To do matrix multiplication, we have to access each element of B N times. It doesn't matter in what order we access the elements, as long as we pair up the right dot product with the right element of C. The way it is illustrates here, we are accessing only one element of each row of B before moving on to the next row. Thus, there is no spatial locality in the references to b.

How can we change the program to have more spatial locality? One way is to rewrite out function to use the transpose of B instead:

void matrix_multiply2 (float A[N][K], float B[K][M], float C[N][M]) {
	float Bt[M][K];
	int     i, j, l;

	// Bt is the transpose of B

	for (i=0; i<K; i++) for (j=0; j<M; j++) Bt[j][i] = B[i][j];

	// now we work with Bt instead of B

        for (i=0; i<M; i++) for (j=0; j<N; j++) {
                C[i][j] = 0.0;
                for (l=0; l<K; l++)
                        C[i][j] += A[i][l] * Bt[j][l];
        }
}

Now the function accesses Bt with a very high degree of spatial locality, since it accesses every element of one row of Bt before moving on to the next row. Interestingly, the new function executes more instructions and consumes more memory, but will take much less time on a real processor (I have measured a factor of 2 speedup with this function for large values of K).

This was a very simple example of how locality affects performance. Compilers are able to transform more complex codes using blocking, tiling, loop fusion/fission, and other optimizations to get more locality.

Let's quickly think about another example of how we can exploit locality. Suppose you need to execute a certain number of independent transactions, e.g., queries that, say, read a database or search engine, or maybe simulate a time step in some simulation for a given set of inputs. The transactions have the following properties:

Transactions are buffered in a queue, and arrive as fast as we can process them.
Each transaction is composed of several phases that each exercise different sets of data.
Transactions don't depend on one another
We are interested in maximum throughput; response time for a given transaction is not as important.

If we evaluate one transaction after another, so that we execute each phase one after another, we are walking all over memory and likely giving the cache a hard time. However, if we rearrange the program, we could do the following:

Read N transactions from the queue into a buffer, where N is a number we fine-tune empirically.
Run the first phase of the transaction on each of the N transactions.
Run the second phase on each transaction, and so forth.
Once the final phase has been done on each transaction, go back to Step 1.

Cache Organization

Caches are organized as blocks of bytes. When data is transferred from main memory to the cache, or from the cache to main memory, it is transferred as a block. Blocks are typically larger than a memory word because of spatial locality and the fact that subsequent accesses to consecutive memory locations are faster than the first access in main memory.

The following questions give a high-level overview of the issues related to caches:

Block placement. Where can a block be placed in the cache?
Block identification. How is a block found in the cache?
Block replacement. Which block should be replaced on a miss?
Write strategy. What happens on a write?

Each question has more than one possible answer.

Block Placement

There are three types of policies regarding block placement:

Direct mapped. In a direct mapped cache, there is only one place a particular block can go. Let N be the number of blocks in the cache. A block at memory address x is typically mapped to the block given by x modulo N. Think of this as a hash table where collisions are solved by evicting an element from the table.
Fully associative. In a fully associative cache, the block can go anywhere in the cache.
Set associative. A set associative cache is composed of many sets. A set contains a certain number of blocks. For instance, a 4-way set associative cache would consist of many sets of four blocks each. Suppose there are N sets. A block from memory address x is mapped onto a set with a hash function, like x modulo N. The block can be placed in any one of the blocks in the set. This organization is halfway between direct mapped and fully associative.

Suppose a cache has N blocks. Then a direct mapped cache can be though of as 1-way set associative cache with N sets, and a fully associative caches can be thought of as a N-way set associative cache with one set.

Why do you think we have these different kinds of organizations? What are the advantages and disadvantages of each?

Block Identification

Suppose we are looking for the data at memory address x in the cache. Once we arrive at the right set or block in the cache, how do we know whether it contains that data, or some other data?

Besides data, each block has a tag associated with it the comes from the address for which it holds the data. A block also has a valid bit associated with it that tells whether or not the data in that block is valid. An address from the CPU has the following fields used to refer to data in the cache:

Block address. This is the portion of the address used to identify the block to the cache. It is divided into two portions:
- Set index. This portion indicates the set in the cache.
- Tag. This portion is stored with the block, and compared against when the cache is accessed.
Block offset. This is the portion used to identify individual words or bytes within a block.

For example, let's say we have a 4-way set-associative cache with 256 sets, and each set is 64 bytes. Thus, it can contain 64KB of data. A 32-bit address from the CPU is divided into the following fields:

Bits 0 through 5: Block index
Bits 6 through 13: Set index
Bits 14 through 31: Tag

How many bits of SRAM will be needed for this cache? Each block has 64 bytes = 512 bits of SRAM, plus one valid bit, plus 18 bits for the tag = 531 bits. There are 256 sets of 4 blocks each, giving 543744 total bits, or about 66.4KB. So about 4% of the bits in the cache are for overhead.

Block replacement

When a cache miss occurs, we bring a block from main memory into the cache. We have to have a policy for replacing some block in the cache with the new block.

What is the policy for a direct mapped cache?

For caches with some amount of associativity, the following policies have been used:

Random. A pseudorandom number generator gives the identity of the block to be replaced within a set. This spreads replacements uniformly through the set, and is cheap to implement.
Least-recently used (LRU). The block that was access least recently within the set is replaced. This assumes that data that haven't been used recently won't be used again in the near future.
First in, first out (FIFO). This approximates LRU by replacing the block that was replaced least recently, rather than accessed least recently. This is cheaper to implement than LRU.

What do you think the effect of these policies is? Why not just always use random, since it is cheap?

Write Strategy

When a write to memory comes from the CPU, there are two basic policies the cache can use:

Write through. The data is written to the cache as well as to main memory.
Write back. The data is stored in the cache only. The data is only written back to memory when the block is replaced.

To implement write-back, each block has another bit of metadata associated with it called a dirty bit. When the block is first fetched from main memory, the dirty bit is cleared to 0. When the block is modified, the dirty bit is set to 1. When the block is replaced, it is written out to main memory only if the dirty bit is set to 1.

What are the advantages and disadvantages of these two policies? How do they affect bus traffics and multiprocessor systems?

Cache Technology

How do caches store data? Caches are made from matrices of SRAM cells. Let's consider, for simplicity, a direct mapped tagless cache of 16 kilobits It is arranged as a 128 x 128 matrix of SRAM cells.

An index into the cache is 14 bits wide.
This index is divided into 7 row address lines and 7 column address lines.
The 7 column address lines are input to a column selector that precharges one of the 128 column select lines to 1.
The 7 row address lines are input to a row decoder that sends Vdd to one of the 128 row select lines.
The SRAM cell that has both its column select and row select lines set to Vdd is selected for reading or writing.
The transistors for each SRAM cell are very small so they can be packed tightly. This causes them to be somewhat slow to read, because it takes a long time for them to drive the output lines; special tricks are used to mitigate this latency.

Let's look at what happens at the transistor level when a bit is read. Here is a diagram of a six transistor (6T) SRAM cell:

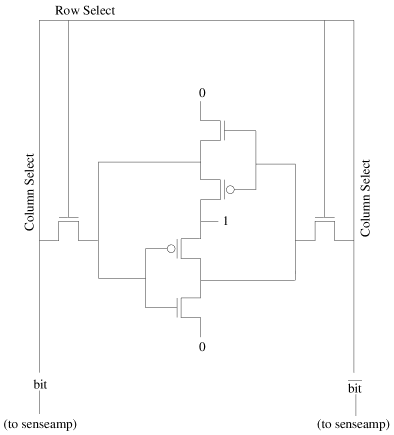
The two inverters (i.e., the four middle transistors) provide storage for a single bit. Think of the bit as continously going around and around the two inverters in a counter-clockwise manner. The bit is the output of the top inverter, and the complement of the bit is the output of the bottom inverter as well as the input to the top inverter. The following occurs when we want to read the bit stored in this SRAM cell:

There are actually two column select lines. Each one is precharged to 1 by the column selector logic. All other column select lines in the cache are set to 0.
The row select line for this cell is set to 1 by the row decoder logic. All other row select lines are set to 0.
At this point, the current from the row select line flows to two NMOS transistors which begin to allow the bit and its inverse to flow out of the SRAM cell to the column select lines. One of the column select lines is slowly pulled to 0. The process is slow because the tiny SRAM transistors have to drive the substantial column select lines that have been precharged to 1. A senseamp at the bottom of the column select lines quickly detects any difference in current and decides that the bit is a 0 if the left column select line is going to 0, or a 1 if the right column select line is going to 0.

The following occurs if we want to write a bit x to the SRAM cell:

The row select line is set to 1, allowing current to flow between the column select lines and the inverters.
The left column select line is driven to x and the right line is driven to the complement of x. The beefier drivers are stronger than the inverters, so the value currently going around the inverters is replaced with the new value.
Other columns in the same row are set to a level of current we can think of as being somewhere between 0 and 1. The result is that those inverters not column-selected simply keep the values they had before.

For next time, we will continue in Chapter 5.