 (n2) algorithm
is faster than a
(n2) algorithm
is faster than a
 (n3) algorithm
for all values of n.
(n3) algorithm
for all values of n.
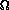 (2n)
(2n)
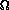 (n) steps.
(n) steps.
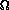 (n 2n) time.
(n 2n) time.
 (n2) algorithm
is faster than a
(n2) algorithm
is faster than a
 (n3) algorithm
for all values of n.
(n3) algorithm
for all values of n.
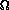 (2n)
(2n)
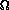 (n) steps.
(n) steps.
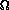 (n 2n) time.
(n 2n) time.
void matrix_add1 (int A[], int B[], int n) {
int i, j;
for (i=0; i<n; i++) for (j=0; j<n; j++)
A[i] = A[i] + B[i];
}
void matrix_add2 (int A[], int B[], int n) {
int i, j;
for (j=0; j<n; j++) for (i=0; i<n; i++)
A[i] = A[i] + B[i];
}
Which one will take less time for large values of n, and why?
Assume they are compiled with no optimizations.
Problem: YESNote that the answer is always "yes." This problem is not NP-hard. Why not?
Instance: A positive integer n
Question: Is it true that either n is odd or n is even?
Problem: TSPConsider the following greedy algorithm for solving TSP:
Instance: A graph G=(V,E), a function w:E -> R giving the weight of an edge, a vertex v0 in V and a number k in R.
Question: Is there a path through G starting at vertex v0 such that the length of that path is at most k?
Greedy-Solve-TSP (G, v0, k) length = 0 unmark all the vertices mark v0 as visited u = v0 while there exist unmarked vertices do: find an unmarked vertex w such that the f (u, w) is a minimum, i.e., find the closest unmarked vertex w to u sum = sum + weight of (u, w) mark w as visited end while sum = sum + weight of (w, v0) if sum <= k then return "yes" else return "no" end ifAssume "marking" is done with an extra Boolean field in the data structure for each vertex.
B-Tree-Search (x, k) // search starting at node x for key k
i = 1
while i <= n[x] and k > keyi[x] do
i++
end while
if i <= n[x] and k = keyi[x] then
return (x, i)
if leaf[x] then return null
Disk-Read (ci[x])
return B-Tree-Search (ci[x], k)
What is a tight asymptotic upper bound, in terms of the minimum degree
t and the number of keys in the entire B-Tree n,
on the number of times the statement i++ is executed?
i 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 v[i] 0 0 3 3 2 0 4 8 8 7 0 6 10 7 13 12v[0..15] represents disjoint sets from the Union/Find with path compression algorithm.