 (ln (n!)).
In Chapter 2.12, we see that a lower bound on the factorial
function is:
(ln (n!)).
In Chapter 2.12, we see that a lower bound on the factorial
function is:
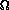 (n ln n).
Can we do any better than this? Is it just a weird coincidence that
all of these "efficient" sorts have the same lower bound asymptotic
performance?
(n ln n).
Can we do any better than this? Is it just a weird coincidence that
all of these "efficient" sorts have the same lower bound asymptotic
performance?
{ a b c }
/ \
/ \
/ \
a < b / \ a > b
/ \
{ a b c } { b a c }
b < c / \ b > c a < c / \ a > c
/ \ / \
{ a b c } { a c b } { b a c } { b c a }
/ \ / \ / \
A general purpose sort is a sorting algorithm that works on
any kind of ordered data. You provide the algorithm with an ordering
on the data, and the algorithm sorts them for you. It is thought that
a general purpose sort and a comparison sort are the same thing.
You provide the comparison sort with a way to compare two items of
data and the algorithms sorts them for you. The standard C function
qsort is a good example of a general sort:
#include <stdlib.h>
void qsort(void *base, size_t nel, size_t width,
int (*compar) (const void *, const void *));
 (ln m).
(ln m).
How many nodes are there in the decision tree for an array of size n?
Since there is a node for every permutation of the array, there are
n! nodes (i.e., n-factorial, n *
(n-1) * (n-2) * (n-3) * ... * 1 nodes). So
the height of the decision tree is
 (ln (n!)).
In Chapter 2.12, we see that a lower bound on the factorial
function is:
(ln (n!)).
In Chapter 2.12, we see that a lower bound on the factorial
function is:
(2for all n. If we take logarithms on both sides and use the properties that log ab = log a + log b and log a/b = log a - log b, and some asymptotic notation to hide constants, we get:n)1/2 (n/e)n <= n!
which works out to simply(1) + ln n + n ln n -
(n) <= ln (n!)
ln (n!) =So the height of the decision tree has a lower bound of(n ln n)
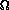 (n ln n).
In the worst case, the sorting algorithm will have to "search"
all the way down to a leaf node, so
(n ln n).
In the worst case, the sorting algorithm will have to "search"
all the way down to a leaf node, so
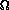 (n ln n)
comparisons is the best a comparison sort can be expected to do.
Since the number of comparisons is at least the number of array
accesses or other operations, this is the lower bound on the
worst case time-complexity of any comparison sort.
(n ln n)
comparisons is the best a comparison sort can be expected to do.
Since the number of comparisons is at least the number of array
accesses or other operations, this is the lower bound on the
worst case time-complexity of any comparison sort.
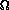 (n) lower bound
time complexity; it has to at least examine all n
elements of the array before it can guarantee they are sorted.
So this is definitely "the best we can do." Are there any sorts
that realize this optimistic time complexity? As we have just seen,
comparison sorts, which correspond to the notion of a general
purpose sort, must take at least
(n) lower bound
time complexity; it has to at least examine all n
elements of the array before it can guarantee they are sorted.
So this is definitely "the best we can do." Are there any sorts
that realize this optimistic time complexity? As we have just seen,
comparison sorts, which correspond to the notion of a general
purpose sort, must take at least
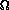 (n ln n)
time in the worst case. But there are sorts that work on specialized
data that work even faster.
(n ln n)
time in the worst case. But there are sorts that work on specialized
data that work even faster.
 (n) time,
and filling the array takes another
(n) time,
and filling the array takes another  (n),
so the whole time to sort is simply
(n),
so the whole time to sort is simply
 (n).
We can generalize this notion to sort an array where the elements
come from a set of small integers. This is the idea behind
counting sort (note that this is different than the version
in the book).
(n).
We can generalize this notion to sort an array where the elements
come from a set of small integers. This is the idea behind
counting sort (note that this is different than the version
in the book).
// A is the array to sort.
// The array elements may be in the set of integers [0..k].
// C is an array from [0..k]; C[i] will tell how many times i occurs in A
Counting-Sort (A, k)
for i in 0 to k do
C[i] = 0 // all counts are initially 0
end for
for j = 1 to length(A) do
C[A[j]]++ // count each element
end for
// C[i] is now the # of times
// i occurs in A
i = 1 // i is the index in A[1..length(A)]
j = 0 // j is the index in C[0..k]
while j <= k do // while we have more elements...
if C[j] != 0 then // if there are more j's in A
A[i++] = j // place a copy of j into A
C[j]-- // one less j
else
j++ // next item in order
end if
end while
This sort takes  (k+n) time: the times to process C
and A.
If k is a small constant, particularly small compared to the
values of n we expect to see (i.e., k =
O(n)), then this sort takes
(k+n) time: the times to process C
and A.
If k is a small constant, particularly small compared to the
values of n we expect to see (i.e., k =
O(n)), then this sort takes
 (n) time. We require
only "constant" storage and time to store and process the array C.
This sort is very sensitive to the kinds of data to be stored; they must
be integral (like integers and characters) and they must be in a
very small range. Sorting even moderate sized integers, like 32-bit
integers in the range
-2e9..2e9, is just impossible because the array C would have to contain
four billion elements. Of course, we can forget about sorting floats
altogether; what is C[3.14159]? But if we're sorting, say, the ages (in years)
of people at UTSA, where k is around 100 and n is
in the several thousands, counting sort would be much faster than
any of the
(n) time. We require
only "constant" storage and time to store and process the array C.
This sort is very sensitive to the kinds of data to be stored; they must
be integral (like integers and characters) and they must be in a
very small range. Sorting even moderate sized integers, like 32-bit
integers in the range
-2e9..2e9, is just impossible because the array C would have to contain
four billion elements. Of course, we can forget about sorting floats
altogether; what is C[3.14159]? But if we're sorting, say, the ages (in years)
of people at UTSA, where k is around 100 and n is
in the several thousands, counting sort would be much faster than
any of the
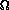 (n ln n)
sorts.
It turns out we can use a stable version of counting sort as the basis for another
sort called radix sort that can sort a much wider range
of data, like character strings and numbers with small decimal
representations.
(n ln n)
sorts.
It turns out we can use a stable version of counting sort as the basis for another
sort called radix sort that can sort a much wider range
of data, like character strings and numbers with small decimal
representations.