Lecture 8

Quicksort

Another sorting algorithm is Quicksort. It uses the same basic divide-and-conquer strategy as merge sort, but instead of completely sorting two subarrays and then merging them back together, it does a simpler operation on the two subarrays.

Here is the Quicksort algorithm, to sort an array A from indices p through r:

Quicksort (A, p, r)
	if (p < r)
		q = Partition (A, p, r)
		Quicksort (A, p, q)
		Quicksort (A, q+1, r)

q is an index into the array A between p and r. q is expected to lie roughly halfway between p and r, so that when Quicksort is called recursively, the subarrays A[p..q] and A[q+1..r] are about the same size.

If p is less than r, then the subarray can be of size no more than 1. This is the base case of the recursion; an array of size 1 is by definition sorted.

Partition is an algorithm that separates A[p..r] into A[p..q] and A[q+1..r], returning the index q. Partition ensures that everything in the "left hand" side of the array, i.e., A[p..q], is less than or equal to A[q], and everything in the "right hand" side, i.e., A[q+1..r], is greater than or equal to A[q]. The "middle" element A[q] is called the "pivot" element since it is around this element the array is turned. The best choice for the pivot element is the median of all elements in A[p..r]. That way, we are assured that the array is divided into two even halves. However, computing the median is costly. The following pseudocode for Partition works very quickly, but may possibly divide the array in a less-than-optimal way:

Partition (A, p, r)
	x = A[p]		// choose first element x in subarray
				// as the pivot; this is a quick
				// (if wildly inaccurate) estimate
				// of the median.

	i = p-1			// i is the index just to the left of
				// the pivot
	j = r+1			// j is the index just to the right of
				// the pivot

	while True do		// loop forever
		repeat
			j--	// keep decrementing j until we reach
				// a point where A[j] doesn't belong
				// there, i.e., is <= the pivot
		until A[j] <= x

		repeat 		// keep incrementing i until
				// A[i] is >= the pivot
			i++
		until A[i] >= x

		if i < j
				// at this point, we have that i and j
				// are two elements, both in the wrong
				// place; if we swap them, they will
				// both be in the right place
			exchange A[i] with A[j]
		else
				// if i >= j, then we are done
				// because we have met in the middle
			return j // return with the index of the pivot
	end while

This algorithm searches the two subarrays separated by the pivot (without knowing beforehand what the index of the pivot will turn out to be) for pairs of elements that are not in the right place, e.g., greater than the pivot but in the left hand side. When it finds such a pair, it swaps them, putting them both in the correct subarray. When the search for elements that are too big meets the search for elements that are too small, we have found the index where the two halves split and we are done with Partition.

So the way Quicksort works is this:

If the array has one or fewer elements, we're done.
Choose a value q to be the first element in the array.
Divide the array into a left half, where everything is less than or equal to q, and a right half, where everything is greater than or equal to q.
The two arrays are now independent of each other in terms of sorting; nothing in the left half belongs in the right have and vice versa. Recursively sort the two halves, then we're done.

Let's look at an example of Partition on some data:

x = A[p] = 5
Array index:          i p		r j
Array contents: 	5 4 6 7 2 3 8 1 9	initial state

		        i             j
			1 4 6 7 2 3 8 5 9	swapped 1 with 5

		        p   i     j     r
			1 4 3 7 2 6 8 5 9	swapped 6 with 3

		        p     i j       r
			1 4 3 2 7 6 8 5 9	swapped 7 with 2

		        p     j i       r
			1 4 3 2 7 6 8 5 9	i exceeds j; we're done.
Everything in A[p..j] is less than 5.
Everything in A[i..r] is greater than or equal to 5.

Best-Case Analysis of Quicksort

The Partition procedure looks at

(1) array elements each time through the while True loop. This loop proceeds until i reaches j, i.e., until all elements of A[p..r] have been visited. This is r - p + 1 elements; if we call this quantity n, Partition takes

(n) time. Initially, the first instance of Quicksort calls Partition on the entire array, where n is the number of elements to be sorted.

To analyze Quicksort, we must first make an assumption that may or may not be true in practice. We must assume that x is always a good estimate of the median so that q ends up halfway from p to r. If this is true, then Quicksort behaves asymptotically exactly like merge sort. The time it takes can be characterized by:

T(n) =

(n) + 2T(n/2) if n >= 1,
0 otherwise.

By a very similar argument to that used in Lecture 2, we find that this time is

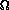(n ln n) .

If we assume that all the elements of A are uniformly randomly distributed, then we are likely to see this 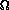(n ln n) behavior. Even if the array is consistently split into one subarray of size 10% n and the other of 90% n, we will still see 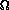(n ln n) time, although in the rigorous analysis we will find a log base 10 term instead of log base 2, making the constant absorbed into the big-Omega somewhat larger.

Worst Case Analysis

In practice, data is often not uniformly randomly distributed. For instance, data may be presented to the algorithm in an almost-sorted manner. Consider the San Antonio telephone book. Each year it must be updated with new names. Maybe all the names and numbers are kept in a file, and the new names are added to the end. When it comes time to print the new phone books, a Quicksort is performed on all the names. Most of the names are already in order, so picking the pivot as the beginning of the array will cause all the subarrays to be extremely lopsided.

More formally, in the case of an array that is already sorted, the pivot will always remain at the beginning of the subarray, giving a left-hand subarray of size 1 and right-hand subarray of size n-1. This gives us a time of:

T(n) = T(n-1) + (n)

Once you count up all the recursive calls to Quicksort, this works out to:

n
( k)
k = 1

which gives us

((n(n+1))/2) =

(n²).

That's just as bad as bubble sort or selection sort. Even worse, because bubble sort runs in time O(n) on already-sorted data. We can try to remedy this by picking different values for the pivot and tweaking Partition to try to predict what the best pivot will be, but there will always be some degenerate case that will exhibit this worst-case behavior. Another approach is to pick the pivot randomly. This way, the probability of the worst-case performance happening shifts from the very high chance that the data will already be somewhat sorted to the very low chance that we will pick an extremely unlikely sequence of random numbers. Let's make a new version of Partition that uses a function Random(a,b) returning a random number from a through b:

Randomized-Partition (A, p, r)
	i = Random (p, r)
	exchange A[p] with A[r]
	return Partition (A, p, r)

This way, the pivot could be anything in the array, and has a much better chance of being near the median even in already-sorted data.

The standard C function qsort() is a randomized version of Quicksort. It is very fast and sufficient for all but the most specialized sorting applications.

Another tweak to Quicksort has been to use something like selection sort when the number of elements goes below some empirically determined threshold. For some small values of n, selection sort might actually be faster than Quicksort, which has a high overhead because of all the recursion and Partitioning. The new tweaked version would look something like:

Quicksort (A, p, r)
	if (r - p < threshold)
		Selection-Sort (A, p, r)
	else
		q = Partition (A, p, r)
		Quicksort (A, p, q)
		Quicksort (A, q+1, r)