Lecture 7
Priority Queues
A priority queue is a data structure for maintaining a set of elements,
each with an associated value called a key. In a normal queue,
elements come off in first-in-first-out order, so the first element in
the queue is the top element. In a priority queue, the element with
the largest key is always on the top, no matter what order it or
the other elements were inserted. Some uses for priority queues:
- Dÿkstra's Algorithm. This algorithm solves the single-source
shortest-paths problem on a weighted digraph. The algorithm uses a priority
queue to consider edges of the graph in order of increasing weight (the key
used can be the negated weight).
- Huffman's Algorithm. This algorithm builds a tree representing the
optimal prefix code given a given the frequency for each symbol. This
code can be used to compress data, sometimes with a significant reduction
in the amount of storage needed. A priority queue is again used to select
the next symbol to assign a code.
- Operating System Scheduling Algorithms. Some processes in an operating
system run with higher priority than others. For instance, an interactive
'vi' session should run with higher priority than a background numerical
simulation, to provide the user with a reasonable interactive response time.
This isn't only nice, it is neccessary to prevent starvation of essential
system services. Putting processes that are ready to run on a priority queue
ensures that the scheduler will pick the process with highest priority to
run next.
Priority Queue Operations
The following operations are defined on priority queues (assumed to be
initially empty sets):
- Insert (S, x) inserts x into the
set.
- Maximum (S) returns the element of S with
largest key.
- Extract-Max (S) removes and returns the element
with largest key.
Naive Implementation
A naive implementation of these operations is to represent the queue
as a linked list L:
- Maximum looks at each element of the list, keeping track
of and finally returning the maximum element.
Naive-Max (L)
M = L
max = head (M)
while M is not empty
if (head(M) > max) max = head(M)
M = tail(M)
end while
return max
If the list has n elements, this algorithm is
 (n) since it must iterate
exactly n times.
(n) since it must iterate
exactly n times.
- Extract-Max does the same thing, but also deletes the element
it finds:
Naive-Extract-Max (L)
do the Naive-Max algorithm, deleting and returning the
element from the list
Since only  (1) work is needed to delete an element from a
reasonably implemented linked list, this algorithm is also
(1) work is needed to delete an element from a
reasonably implemented linked list, this algorithm is also
 (n).
(n).
- Insert just puts the element onto the linked list.
Naive-Insert (L, key)
M = new node with key
tail(M) = L
L = M
This does  (1) work since we're not worried about keeping the
list in any order.
(1) work since we're not worried about keeping the
list in any order.
Heap Implementation
We can use a heap to improve the implementation, since a heap always keeps
its maximum element in the first element:
- Maximum just returns the top element of the heap.
Heap-Maximum (A)
return A[1]
With exactly one array access, the time is simply  (1), compared
with
(1), compared
with  (n) for the naive priority queue.
(n) for the naive priority queue.
- Insert increases the size of the heap, then chases up the
tree looking for the right place for the new element in a way similar to
Heapify:
Heap-Insert (A, key)
heap-size(A)++ // increase heap size
i = heap-size(A) // i is last index in heap
while (i > 1) and (A[Parent(i)] < key) // while new element is
// still too big...
do
A[i] = A[Parent(i)] // swap parent down, go
// up one level
i = Parent (i)
end while
A[i] = key // key is in right place
This could possibly go from a leaf up to the root, taking
O(height) = O(lg n) time, compared
with O(1) of the naive version. This is a little worse, but
as we will see, that doesn't matter too much. Note: we
might actually see 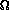 (lg n)
performance if we keep extracting the maximum and then inserting it back
into the heap, because we expect to have to swap all the way from a
leaf to the root.
(lg n)
performance if we keep extracting the maximum and then inserting it back
into the heap, because we expect to have to swap all the way from a
leaf to the root.
- Extract-Max essentially does one round of the Heapsort
loop, removing the top of the heap, swapping the last element into its place,
then Heapifying:
Heap-Extract-Max (A)
if (heap-size(A) < 1)
error "heap underflow" // woops, empty heap!
max = A[1]
A[1] = A[heap-size(A)] // move last element to root
heap-size(A)--
Heapify (A, 1) // make it a heap again
return max
Everything is O(1) except for the call to Heapify, which
we know is O(lg n).
Let's compare the two implementations in a table:
Naive vs. Heap-based Priority Queues
| Type of Queue |
Time for Maximum |
Time for Insert |
Time for Extract-Max |
|---|
| Linked List |
 (n) (n) |
 (1) (1) |
 (n) (n) |
| Heap Based |
 (1) (1) |
O(lg n) |
O(lg n) |
Using a heap-based priority queue looks good, but should it bother us
that Heap-Insert takes O(lg n) time while
Naive-Insert takes only  (1) time? No: Most algorithms
that use a priority queue, like those mentioned above, will either leave
the queue empty at the end or reach a steady state where the same number
of items enter the queue as leave the queue. Thus, for every call to
Insert, there must be a corresponding call to Extract-Max.
Any advantage the naive implemenation gains with its
(1) time? No: Most algorithms
that use a priority queue, like those mentioned above, will either leave
the queue empty at the end or reach a steady state where the same number
of items enter the queue as leave the queue. Thus, for every call to
Insert, there must be a corresponding call to Extract-Max.
Any advantage the naive implemenation gains with its  (1)
Insert is quickly lost when it has to do a
(1)
Insert is quickly lost when it has to do a  (n)
Extract-Max.
(n)
Extract-Max.
Also, a linked list may grow arbitrarily large, while the heap owes much
of its speed advantage to its implementation in a fixed-sized array. We
may, from time to time, have to reallocate the heap's array to accomodate
more elements. Reallocating may take O(n) time.
Will this eat up our  (lg n)
advantage with Insert? Yes, if we have to reallocate every time
we do an Insert. But if we are smart, we will double the
size of the array each time we reallocate, anticipating future Inserts.
This will allow us to do only
up to O(lg n) reallocations during a program run, preserving
the heap's asymptotic advantage.
(lg n)
advantage with Insert? Yes, if we have to reallocate every time
we do an Insert. But if we are smart, we will double the
size of the array each time we reallocate, anticipating future Inserts.
This will allow us to do only
up to O(lg n) reallocations during a program run, preserving
the heap's asymptotic advantage.
Note: if the number of different priorities is a small constant
k, then using an implementation based on having an array of
k linked lists might give better performance than the heap-based
priority queue. Such is the case with operating system schedulers with
a small number of priorities, e.g., "system," "user," and "background"
(k=3).
 (n) since it must iterate
exactly n times.
(n) since it must iterate
exactly n times.
 (1) work is needed to delete an element from a
reasonably implemented linked list, this algorithm is also
(1) work is needed to delete an element from a
reasonably implemented linked list, this algorithm is also
 (n).
(n).
 (1) work since we're not worried about keeping the
list in any order.
(1) work since we're not worried about keeping the
list in any order.
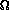 (lg n)
performance if we keep extracting the maximum and then inserting it back
into the heap, because we expect to have to swap all the way from a
leaf to the root.
(lg n)
performance if we keep extracting the maximum and then inserting it back
into the heap, because we expect to have to swap all the way from a
leaf to the root.