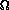 (g(n)) = {
the set of all f such that there exist positive constants
c and n0 satisfying
0 <=
cg(n)
<
f(n)
for
all n >= n0 }.
(g(n)) = {
the set of all f such that there exist positive constants
c and n0 satisfying
0 <=
cg(n)
<
f(n)
for
all n >= n0 }.
When comparing the running times of two algorithms, these lower order terms are unimportant when the higher order terms are different. Also unimportant are the constant coefficients of higher order terms; an algorithm that takes a time of 100n2 will still be faster than an algorithm that takes n3 for any value of n larger than 100. Since we're interested in the asymptotic behavior of the growth of the function, the constant factor can be ignored.
Let's define big-Oh more formally:
O(g(n)) = { the set of all f such that there exist positive constants c and n0 satisfying 0 <= f(n) <= cg(n) for all n >= n0 }.This means that, for example, O(n2) is a set, or family, of functions like n2 + n, 4n2 - n log n + 12, n2/5 - 100n, n log n, 50n, and so forth. Every function f(n) bounded above by some constant multiple g(n) for all values of n greater than a certain value is in O(g(n)).
Examples:
3n2 + 4n - 2 <= cn2 for all n >= n0 .Divide both sides by n2, getting:
3 + 4/n - 2/n2 <= c for all n >= n0 .If we choose n0 equal to 1, then we need a value of c such that:
3 + 4 - 2 <= cWe can set c equal to 6. Now we have:
3n2 + 4n - 2 <= 6n2 for all n >= 1 .
n3 = O(n2)Then there must exist constants c and n0 such that
n3 <= cn2 for all n >= n0.Dividing by n2, we get:
n <= c for all n >= n0.But this is not possible; we can never choose a constant c large enough that n will never exceed it, since n can grow without bound. Thus, the original assumption, that n3 = O(n2), must be wrong so n3 != O(n2).
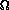 :
:
This gives us a somewhat different family of functions; now i any function f that grows strictly faster than g is in(g(n)) = { the set of all f such that there exist positive constants c and n0 satisfying 0 <= cg(n) < f(n) for all n >= n0 }.
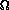 (g). So, for example,
n3 =
(g). So, for example,
n3 =
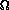 (n2).
(n2).
It is equivalent to say:(g(n)) = { the set of functions f(n) such that f(n) = O(g(n)) and f(n) =
(g(n)) } .
Whenever possible, we try to bound the running time of an algorithm from both above and below with Theta notation.(g(n)) = { the set of all f such that there exist positive constants c1, c2 and n0 satisfying 0 <= c1g(n) <= f(n) <= c2g(n) for all n >= n0 }.
 (p(n)).
(p(n)).
 (max (p(n), q(n)) .
(max (p(n), q(n)) .
 )n) for any
constant k and any positive constant
)n) for any
constant k and any positive constant
 (i.e., any polynomial is
bounded by any exponential).
(i.e., any polynomial is
bounded by any exponential).
Readings: Read Chapters 4, 6 and 7 in the book.