Lecture 16

Greedy Algorithms continued: Dÿkstra's Algorithm

(This is in Section 24.3 of the book, but has a lot to do with greedy algorithms.)

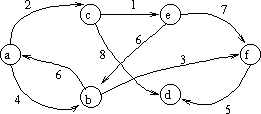
Consider a weighted, directed graph G = (V, E, w). V is the set of vertices. E is the set of edges that are ordered pairs linking the vertices. w is a function from E to the real numbers giving the weight of an edge.
For example, in the following graph:

picture of a graph
we have: In a practical application, the graph might represent cities and distances between them in terms of airplane ticket cost, road miles, or some other metric. Another example would be Internet nodes connected by transmission lines of different speeds.

A path through the graph is a sequence of vertices that are connected by edges. For instance, (a, b, f, d) is a path connecting vertex a to vertex d. The length or cost of a path is the sum of all the weights of the edges traversed. The length of (a, b, f, d) is w(a, b) + w(b, f) + w(f, d) = 4 + 3 + 5 = 12. Another path is (a, c, d), with length 2 + 8 = 10, so some paths are longer than other.

We would like to know, given a single source vertex, what the length of the shortest path to any other vertex is. This is the single-source shortest paths problem. It can be solved with a greedy algorithm called Dÿkstra's Algorithm.

In the algorithm, we will arrange V as an sequence from 1..n, with vertex #1 being the source vertex. We'll have an array D[2..n] keeping track of the current minimum distances; at any point in the algorithm, D[i] is the current minimum length of a path from vertex #1 to vertex #i. There is a priority queue Q that contains vertices whose priorities are their values in D (smaller value means higher priority). Note that the priority queue must be able to automatically account for adjustments to D, so we'll have to use something a little more sophisticated than a heap (but just a little). 

Dÿkstra (G, s)
	n = the size of V
	for i in 2..n do		// initially, D[i] is the weight
		D[i] = w (1, i)		// of the edge from vertex 1 to i,
	end for				// which might be infinite
	for all i >= 2 in V, insert i into Q,
		using D[i] as the priority
	repeat n-2 times
		v = Extract-Minimum (Q)	// v is the closest vertex to #1
		for each vertex w left in Q do
			D[w] = min (D[w], D[v] + w (v, w))
		end for
	end repeat
	return D
D starts out as the obvious first guess: the length of the edge from 1 to i for i in 2..n. This might not be the best guess, especially if there is no edge and the w function returns infinity. Q starts with all the vertices in it.

In a loop, we greedily go toward the vertex v closest to 1, the minimum element in the queue. At this point, we know the length of the minimum path from 1 to v that doesn't go through any of the vertices in Q. We then update D, offering each other vertex w a possibly shorter path length from vertex 1 via v, i.e., path from 1 --> v --> w. If the length in D is greater than this length, we replace it.

At the end of the algorithm, all vertices but the farthest one from 1 have been removed from the queue, thus D has the lengths of the shortest paths through any vertex.

Let's use the above graph for an example of Dÿkstra's Algorithm starting from vertex a: 

Initially:
Q = { b, c, d, e, f} (think of them as 2..5)
	    b  c  d  e  f
D[2..5] = [ 4  2 oo oo oo ]

repeat loop starts:

minimum v from Q = c, with D[c] = 2.  Now Q = { b, d, e, f }.
Look at path lengths from a through c to { b, d, e, f }
	D[b] = 4,  D[c] + w (c, b) = oo, no change.
	D[d] = oo, D[c] + w (c, d) = 8, so now D[d] = 8 (a->c->d)
	D[e] = oo, D[c] + w (c, e) = 3, so now D[e] = 3 (a->c->e)
	D[f] = oo, D[c] + w (c, f) = oo, no change

          b  c  d  e  f 
Now D = [ 4  2  8  3 oo ]

minimum v from Q = e, with D[e] = 3.  Now Q = { b, d, f }
Look at path lengths from a through e to {b, d, f}
	D[b] = 4, D[e] + w (e, b) = 9, so no change.
	D[d] = 8, D[e] + w (e, d) = oo, so no change
	D[f] = oo, D[e] + w (e, f) = 10, D[f] = 10 (a->c->e->f)

          b  c  d  e  f 
Now D = [ 4  2  8  3 10 ]

minimum v from Q = b, with D[b] = 4.  Now Q = { d, f }
Look at path lengths from a through b to {d, f}
	D[d] = 8, D[b] + w (b, d) = oo, so no change.
	D[f] = 10, D[b] + w (b, f) = 7, so D[f] = 9 (a->b->f)

          b  c  d  e  f 
Now D = [ 4  2  8  3  9 ]

minimum v from Q = d, with D[d] = 8.  Now Q = { f }
Look at path length from a through b to f
	D[f] = 9, D[d] + w (d, f) = oo, so no change.

We are done; f is the only element of the queue, so it can't help make
any other path lengths shorter.

      b  c  d  e  f 
D = [ 4  2  8  3  9 ]

Analysis

An analysis of Dÿkstra's Algorithm depends heavily on the particular implementation of graphs and the priority queues.

If we assume an adjacency matrix representation, then w is just an O(1) array access and Q is a queue of array indices. Storage for an adjacency matrix is (n2). If we know that there are very few edges, an adjacency list representation would be more appropriate. We'll assume a matrix representation for the analysis.

If we want to use a heap-based priority queue, we'll have to call Heapify each time D is updated, which happens O(|Q|) times throughout the repeat loop and takes O(ln |Q|) time for each call.

The initialization of D is (n), the initialization of the queue is O(n ln n) (n inserts into a heap, each costing O(ln n) time).

The repeat loop happens n-2 times. Let e = |E|, i.e., the number of edges. No edge is considered more than once in the for each edge loop, so this is an upper bound on the number of possible updates to D and thus calls to Heapify, which each cost O(ln n) time. We must do an Extract-Minimum each time through the repeat loop, each of which also cost O(ln n) time. So we the algorithm runs in time O(n ln n) (for initializing the queue) + O(n ln n) (for the calls to Extract-Minimum) + O(e ln n) (for all the calls to Heapify when we update D), = max (O(n ln n), O(e ln n)).