There are many implementations of containers. For instance, we could use linked lists, or various kinds of trees. Today we'll see a special kind of container called a hash table. First, let's recall a simple data structure that acts as a container: binary search trees.
struct tree_node {
int k;
struct tree_node *left, *right;
};
void tree_insert (struct tree_node **r, int k) {
if (*r == NULL) {
*r = malloc (sizeof (struct tree_node));
(*r)->left = NULL;
(*r)->right = NULL;
(*r)->k = k;
} else if ((*r)->k < k) tree_insert (&((*r)->right), k);
else if ((*r)->k > k) tree_insert (&((*r)->left), k);
else ; // duplicate key
}
int tree_search (struct tree_node *r, int k) {
if (!r) return 0;
if (r->k < k) return tree_search (r->right, k);
if (r->k > k) return tree_search (r->left, k);
return 1;
}
(Remove is left as an exercise for the reader.)
The analysis of Search is similar. Search traces a path from the root to the sought node, or to some leaf if the node isn't there. In the worst case, this is a path from root to leaf, or O(log n) with an almost complete binary tree.
For completeness let us briefly mention the possible pathological behaviors of a binary search tree. Suppose there is a long run of mostly sorted data inserted into the tree; then most of the insertions will go to the left, and the tree will have linear instead of logarithmic height. Further insertions and searches will then also have linear behavior. However, as mentioned before, there are solutions to this problem that are beyond the scope of the current lecture.
Logarithmic behavior is very good, and we can solve the pathological cases, so what else could we ask from a container class?
To search for a key k in the hash table, we again let i = hash(k) and then look for k in the ith element of A.
If the hash function takes constant time to compute, then clearly both Insert and Search should take O(1) time since all they are doing is computing a constant function and accessing a single array element.
There's just one problem: what if two keys we insert both hash to the same array index? Then we have a collision. There are two main methods for dealing with collisions:
/* here is code for implementing linked lists */
struct list_node {
int k;
struct list_node *next;
};
void list_insert (struct list_node **l, int k) {
struct list_node *p = malloc (sizeof (struct list_node));
p->k = k;
p->next = *l;
*l = p;
}
int list_search (struct list_node *l, int k) {
if (!l) return 0;
if (l->k == k) return 1;
return list_search (l->next, k);
}
/* here is code for the hash table with chaining */
struct hash_table {
int nlists;
struct list_node **table;
};
void hash_table_init (struct hash_table *t, int nlists) {
int i;
t->nlists = nlists;
t->table = malloc (nlists * sizeof (struct list_node *));
for (i=0; i<nlists; i++) t->table[i] = NULL;
}
unsigned int hash (int k, int n) {
return ((k * 233) ^ k) % (unsigned int) n;
}
void hash_table_insert (struct hash_table *t, int k) {
unsigned int h = hash (k, t->nlists);
list_insert (&(t->table[h]), k);
}
int hash_table_search (struct hash_table *t, int k) {
int h = hash (k, t->nlists);
return list_search (t->table[h], k);
}
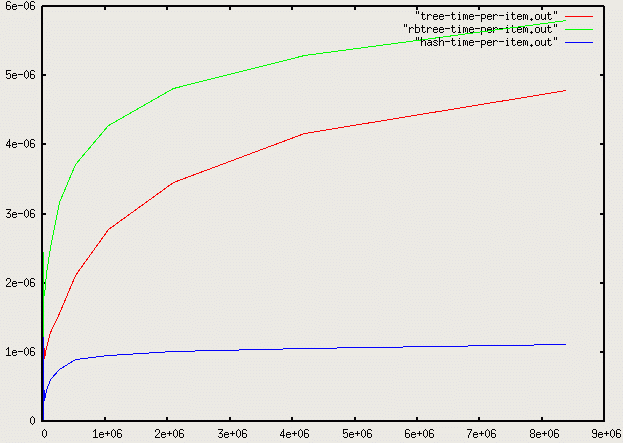
Let's look at a graph of the average access time per element of a program that inserts n numbers into a container and then performs n searches on each of the inserted numbers. We'll look at binary search trees, red-black trees, and hash tables:

Read Chapter 16 and 18.