Miscellaneous: Loops and Numerical Stuff

Here is a program to print a sine wave. Since we don't yet know how to do graphics in C, we'll print a sine wave by having text rows be the x-axis and text columns be the y-axis. Then we'll let an angle theta go through values from -2 Pi through 2 Pi in steps of 0.1, printing an asterisk after a number of spaces proportional to the sine of theta: 
#include <stdio.h>
#include <math.h>

/* AMP is an amplitude by which we'll multiply the sine value;
 * it's the number of columns from the x-axis (the line going down the
 * middle of the screen) to the rightmost part of the screen.
 */
#define AMP  40

/* defining PI */

#define PI 3.14159265358979323844

main () {
        double  theta, sine;
        int     i, nspaces;

	/* let theta step through values from -2PI through 2PI */

        for (theta=-2*PI; theta <= 2*PI; theta += 0.1) {

		/* find the sine of theta, scaled by AMP */

                sine = sin (theta) * AMP;

		/* make that into an integer */

                nspaces = (int) sine;

		/* half of the sine function is negative, so translate
		 * it up by AMP columns
		 */

                nspaces += AMP;

		/* print that number of spaces followed by an asterisk */

                for (i=0; i<nspaces; i++) printf (" ");

                printf ("*\n");
        }
	return 0;
}
This program uses the C sin function to compute the sine of an angle given in radians. The sin function is part of the Standard C Math Library, whose other members are declared along with sin in math.h. When compiling a program that uses the math library, you must link in the math library object files. You do this by appending -lm to your normal cc line, e.g.: 
	cc -o sine sine.c -lm
if you named your program file sine.c.

Here are some math functions from the math library:

Area Under a Curve

Consider the function f(x) = sin x + 1, from x = 0 through x = 2 Pi. The function is greater than 0 everywhere in this range. How would we compute the area underneath the curve? We could use Calculus to find the antiderivative and then apply the fundamental theorem of calculus, but this doesn't work for other functions that don't have a closed-form antiderivative, or if you just don't like Calculus. What we can do is sample the function at uniformly spaced intervals (let's call this interval Delta-x), then draw rectangles from the x-axis to the sampled points. We can then sum up the areas of the rectangles, each of which is just the width, Delta-x, times the height, f(x). In general, if we are looking at the interval on the x-axis from a to b, the following formula:

describes this sum, which approximates the area under the curve. In our case, a = 0 and b = 2 Pi. As we decrease Delta-x, this sum gets more and more precise.

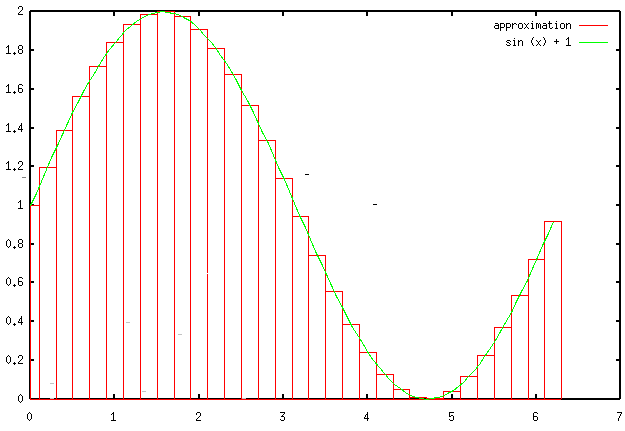
Here's a graph of the function and the rectangles whose sum approximates the area under the curve, with Delta-x = 0.2:
picture of sine wave
Here's a C program that computes the sum: 
#include <stdio.h>
#include <math.h>

#define PI 3.14159265358979323844

int main () {
	double	x, 
		dx, 	/* delta-x */
		a,
		b,
		sum;

	/* use very small delta-x */

	dx = 0.0001;
	a = 0.0;
	b = 2 * PI;
	sum = 0.0;

	/* go through all values of x from 0..2PI, in steps of 0.0001 */

	for (x=a; x<=b; x+=dx) 
		sum += (sin (x) + 1) * dx;

	/* output area */

	printf ("area = %f\n", sum);
	return 0;
}
When this program is run with Delta-x equal to 0.0001, the output produced is this: 
area = 6.283200
Let's think intuitively how this answer might seem right. Take the top portion of the wave, from x = 0 though Pi and y = 1 through 2, and cut it off. Invert it and place it in the convex portion of the side of the function from x = Pi through 2 Pi. You will have a rectangle of height 1 and length 2 Pi, so the area is 2 Pi, or about 6.283185. With a smaller Delta-x, the program's estimate would agree more closely with that figure, but would take longer.