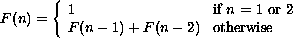More Functions Cont.

The Fibonacci Function

Here's another example of a mathematical function we can code in C. The Fibonacci sequence is a sequence of integers in which each number is the sum of the previous two. The first two are equal to 1. The Fibonacci function is a function F such that F(i) is equal to the ith Fibonacci number:

. So the sequence of numbers goes like this:

and so on. The Fibonacci functions comes up a lot in computer science and also in nature. It turns out that when you divide the nth Fibonacci number by the (n-1)th, you get an approximation to the Golden Ratio, or about 1.618033988, one of those important numbers like Pi and e. The higher the value of n, the better the approximation. Fibonacci numbers also have interesting number theoretical properties. Let's look at a function that computes the nth Fibonacci number:

int F (int n) {
        int     F_i, 		/* the "current" fibonacci number */
		F_i_minus_1, 	/* the "previous" one */
		tmp;		/* temporary */
        int     i;


	/* we start with i=2, so F(i-1) is 1, F(i) is 1 */

        F_i_minus_1 = 1;
        F_i = 1;

	/* we know F(1) and F(2), let's get F(3)..F(n) */

        for (i=3; i<=n; i++) {

		/* tmp is F(i) */

                tmp = F_i_minus_1 + F_i;

		/* F(i-1) is previous value */

                F_i_minus_1 = F_i;

		/* F(i) is current value */

                F_i = tmp;
        }

	/* all done... */

        return F_i;
}

So to get a table of Fibonacci numbers, we can have a simple main like this:

#include <stdio.h>

int main () {
	int	i;

	for (i=1; i<=46; i++) printf ("%d %d\n", i, F(i));
	return 0;
}

(Why 46? F(47) overflows a 32-bit integer; these numbers get big fast.)

Recursion

So far, when we have needed to do something repeatedly, we have done so with the iteration structure of structured programming. This is a characteristic of imperative programming, where step-by-step instructions are given to the computer.

Another way to get the computer to compute something is to simply give it the definition of a function, instead of a step-by-step method to compute it. Iteration can be eliminated by defining a function in terms of a simpler version of itself; this is called recursion, and this goes with a functional style of programming.

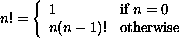For example, the factorial function can be defined n! = 1 if n=0, n(n-1)! otherwise

. Note that this definition is in terms of itself; it is recursive. We've already seen an iterative definition of factorial in C:

int factorial (int n) {
        int     i, product;

        product = 1;
        for (i=1; i<=n; i++) product = product * i;
        return product;
}

But we can just directly code the function from the definition instead of doing the algorithm:

int factorial (int n) {
	if (n == 0)
		return 1;
	else
		return n * factorial (n - 1);
}

So factorial is calling upon itself to figure out values of the factorial function for different values of n. You can think of each invokation of factorial as a separate "copy," with its own n parameter.

In each recursive function, there is a base case that stops the recursion. For factorial, this is when n is equal to 0. Without the base case, a recursive function might keep calling itself ad infinitum with nothing to stop it.

Let's try some more recursion. Remember the program we wrote that asks the user for two numbers, then prints all the integers between the two? We can rewrite it using a function:

#include <stdio.h>

void print_between (int first, int last) {
	int	i;

	for (i=first; i<=last; i++) printf ("%d\n", i);
}

int main () {
	int	n, m;

	printf ("Enter two numbers: ");
	scanf ("%d %d", &n, &m);
	print_between (n, m);
	return 0;
}

So far so good, it's pretty clear what's going on here. Now let's rewrite the print_between function, this time using recursion:

void print_between (int first, int last) {
	if (first <= last) { /* base case */
		printf ("%d\n", first);
		print_between (first+1, last);
	}
}

When we call this function with, say print_between (2, 6), the following sequence occurs:

Function Call			Output
print_between (2, 6);
 printf ("%d", 2);		2
 print_between (3, 6);
  printf ("%d", 3);		3
  print_between (4, 6);
  printf ("%d", 4);		4
   print_between (5, 6);
   printf ("%d", 5);		5
    print_between (6, 6);
    printf ("%d", 6);		6
    return
   return
  return
 return
return

(The returns are where each function call ends.) What good is this? Not much, it's just a contrived example of recursion. But what happens if we switch the order of the printf and recursive function call:

void print_between (int first, int last) {
	if (first <= last) { /* base case */
		print_between (first+1, last);
		printf ("%d\n", first);
	}
}

That simple change causes the function to print the sequence backwards:

Function Call			Output
print_between (2, 6);
 print_between (3, 6);
  print_between (4, 6);
   print_between (5, 6);
    print_between (6, 6);
    printf ("%d", 6);		6
    return
   printf ("%d", 5);		5
   return
  printf ("%d", 4);		4
  return
 printf ("%d", 3);		3
 return
printf ("%d", 2);		2
return

Each recursive function call "remembers" it's own value for last, and prints it out after recursively calling print_between. What good is this? Okay, it's still not much good; we could still do it with stuff we already know like a for loop.

What if we wanted to print a list of numbers the user types in backwards? Say the user types in 4 3 7 5 2, then the computer would print out 2 5 7 3 4. We could do it if we knew how many numbers the user were going to type in, but what if we don't? We could skip ahead to the chapter on arrays, but let's try this using just what we know. We'll have the user type -1 to signal the end of input as we have before:

#include <stdio.h>

void print_backwards (void) {
	float	f;

	/* read in a number */

	scanf ("%f", &f);

	/* if not the end of input... */

	if (f != -1.0) { /* f == -1 is the base case */

		/* recursively get more numbers */

		print_backwards ();

		/* print the current number */

		printf ("%f\n", f);
	}
}

int main () {
	printf ("Enter some numbers, followed by -1: ");
	print_backwards ();
}

Let's take another look at the Fibonacci function, this time recursively:

int F (int n) {
	if (n == 1 || n == 2) return 1;	/* base case */
	return F(n-1) + F(n-2);
}

The old version was about fourteen lines of C code. This is four lines, with no variables. More efficient, right? Wrong; this function takes a lot more time because it needlessly recomputes many factorial values. Although we can try to make this one faster using arrays (from the next chapter), in general recursive functions are a little more time consuming than their iterative cousins. Doing a function call in machine language takes a fair amount of time compared to doing one iteration of a loop, so sometimes recursion is less efficient. Sometimes, though, it is the most natural way of looking at a problem and makes the code more readable.

Please begin reading Chapter 5 in your book.