CSCE 312 Fall 2023
Computer Organization
Lecture 2
Digital Logic Design I
Topics for today:
- Digital signals
- Wires
- Transistors
- Truth tables
- Logic gates
- Symbols for gates
- Logic gates from transistors
- Combinational circuits
- Implementing Boolean functions with digital circuits
- Simulating other gates with NAND
- Computing with logic gates
- Full adder
- Adding two n-bit integers with combinational circuits
Digital signals
Electronic computers use Boolean logic for all computations. We need
something to electrically represent 0 and 1. We use different levels of
voltage, e.g. 0V and +5V. Boolean, i.e. binary, logic is used because
it's easiest to have two levels instead of, say, 10.
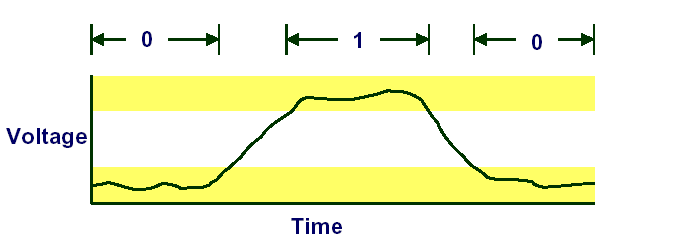
This graph shows an electric signal representing a change from 0 to 1 and
back to 0.
Wires
Wires implement communication of the digital signals in the computer.
Wires transport signals from one place to another. They are made of some
conductive metal. Although they have their limits and can be tricky, it's
OK for us to think of them as being arbitrarily long, narrow, inexpensive,
and fast as we build our mental model of what's going on inside the machine.
Transistors
In a digital computer, transistors are used as the most basic element of
computation. They are connected by wires. Transistors are tiny switches.
They have three terminals:
- Gate (G)
- Drain (D)
- Source (S)
When the gate terminal is triggered, current is allowed to flow from
the source to the drain. Otherwise, no current flows from the source
to the drain. Again, we can think of them for now as being arbitrarily
small, cheap, and fast. Transistors are connected to one another and to
power and ground by wires. Power and ground are concepts we don't really
need for our purposes; they're just necessary for keeping the machine on.
Just think of wires as pipes, like for water, that move information around,
and transistors as faucets that turn the water on and off (1 and 0).
There are two types of metal-oxide semiconductor (MOS) transistors used in the CMOS technology that
dominates current computer architecture:
- NMOS - triggered when 1 is appplied to G.
D
_|
G --||_
|
S
NMOS transistors are good at passing 0's, but not good at passing 1's.
- PMOS - triggered when 0 is applied to G.
D
_|
G -o||_
|
S
PMOS transistors are good at passing 1's, but not 0's.
We'll get back to transistors in a little bit.
Truth Tables
A Boolean function is a function whose domain is a vector of
bits and whose range is one bit. A Boolean function can be completely
described by a truth table giving the values of the function for each
combination of bits in the bit vectors.
Here's a truth table:
a b c f(a,b,c)
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
Logic Gates
Logic gates are physical components that implement logical functions like
AND and OR. They are connected by wires to inputs, other gates, and outputs
(as well as other things we will find out about later). Some important
gates are:
- AND, or &
a b a & b
0 0 0
0 1 0
1 0 0
1 1 1
- OR, or |
a b a | b
0 0 0
0 1 1
1 0 1
1 1 1
- exclusive OR, XOR, ^, or !=
a b a ^ b
0 0 0
0 1 1
1 0 1
1 1 0
- NAND
a b a NAND b
0 0 1
0 1 1
1 0 1
1 1 0
- NOR
a b a NOR b
0 0 1
0 1 0
1 0 0
1 1 0
- NOT, or ~
a ~a
0 1
1 0
Logic gates can have more than two inputs; what would those truth tables
look like?
Symbols for gates
When designing a digital logic circuit, we draw a circuit diagram showing
the various gates and wires connecting them. The following symbols represent
logic gates:
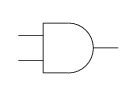
- AND
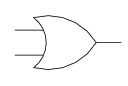
- OR
- XOR
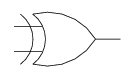
- NAND
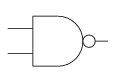
or alternately
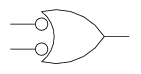
- NOR
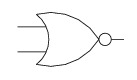
or alternately
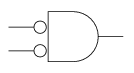
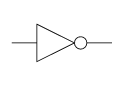
- NOT
Logic gates from transistors
How do we compute with transistors? We'd like to be able to work with AND,
OR, NOT, etc., not with "turn on" and "bad at passing 0."
For example, consider the NOT function:
in out
-- ---
0 1
1 0
Here is an example of a NOT gate (or inverter) implemented with
transistors:
1
_|
|-o||_
___in___| |__out___
| _|
|--||_
|
0
How about a more complex function like NOR? Recall that the truth table
for NOR is:
a b a NOR b
0 0 1
0 1 0
1 0 0
1 1 0
How would we implement this in transistors?
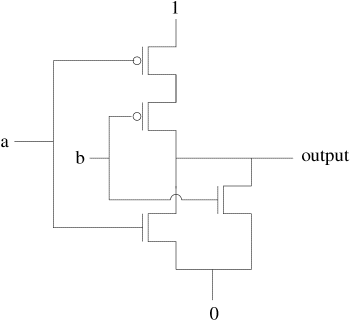
Combinational Circuits
Combinational circuits are acyclic directed graphs whose vertices are inputs, outputs, or gates and whose edges
are wires. They are drawn as circuit diagrams using the symbols we've seen. For instance, here is a
combinational circuit:
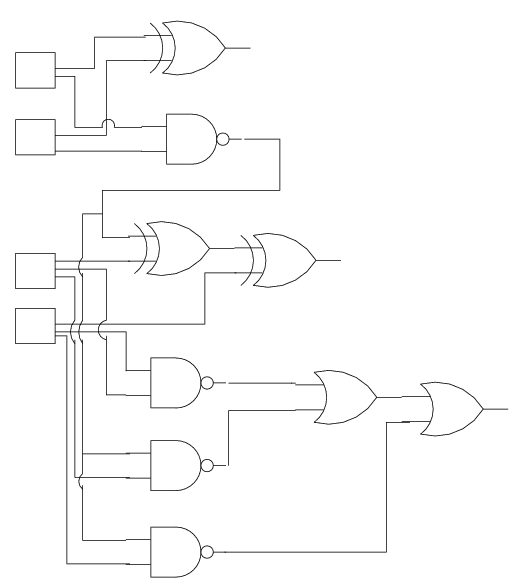
The squares represent inputs to the circuit, while the unattached outputs represent outputs from the
circuit. This circuit happens to be a 2-bit adder.
Implementing Boolean functions with digital circuits
Let's look at an interesting function we might want to compute using digital logic:
a b c f(a,b,c)
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
How would we implement this function with digital logic? First, we have
to figure out a formula that computes this function. How about this:
(a & b) | (b & c) | (a & c)
Yeah, that'll work. Now how do we implement this with logic gates?
Like this:
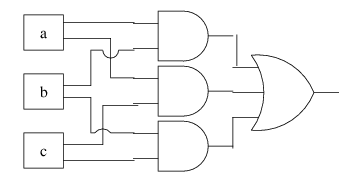
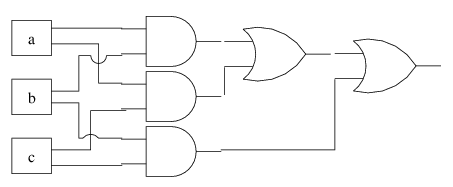 Another way would be to use a 3-input OR gate:
Another way would be to use a 3-input OR gate:
Simulating other gates with NAND
It turns out that NAND is a very useful gate. A 2-input NAND consumes
only 4 transistors, as opposed to AND and OR which each consume 6. Also,
NAND can be used to compute any other logic function, i.e., it is complete
for logic. How could we prove that?
The reasons why there are alternate symbols for NAND (as well as NOR)
is because those bubbles represent NOTs that can be placed in pairs on
wires to make normal ANDs and ORs into NAND (and NORs). For instance, the
circuit we just saw can be drawn with just NANDs like this:
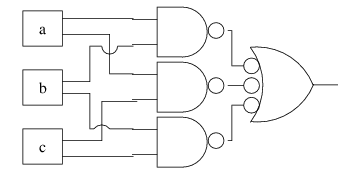
(Note that the 3-input gate is a NAND, just as an OR symbol with two
bubbles on the inputs is a 2-input NAND.)
Computing with logic gates
We can use logic gates to compute with binary numbers; that's how computers
do arithmetic. Imagine how you would design a circuit to do a bitwise OR,
or a bitwise AND.
Majority function
Another useful function to compute would be the majority function: this
function returns 1 if the majority of its inputs are 1, 0 otherwise.
The function we've been with working so far is the 3-input majority function.
Parity function
The parity function is useful for a variety of reasons. It is true if
and only if the number of inputs that are true is odd. How would you
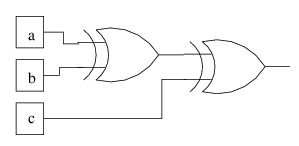
implement this function? Well, it turns out that XOR is the 2-input
parity function. What about the 3-input parity function? Here's the
truth table:
a b c parity(a,b,c)
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1
One way
to implement 3-input parity is using 2 XORs, like this:
Full adder
This brings us to a more useful computation: a full adder circuit.
This circuit takes as input three 1-bit numbers and produces the 2-bit sum,
which can be 0, 1, 2, or 3. It turns out that the least significant
Let's look at a truth table for this function:
a b c c0 s0
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
c0 is the most significant bit of the sum, and s0 is the
least significant bit. Notice anything? The most significant bit is the
majority of the input bits, and the least significant bit is the parity.
So we can build a full adder from parity and majority circuits.
Adding two n-bit numbers with combination circuits
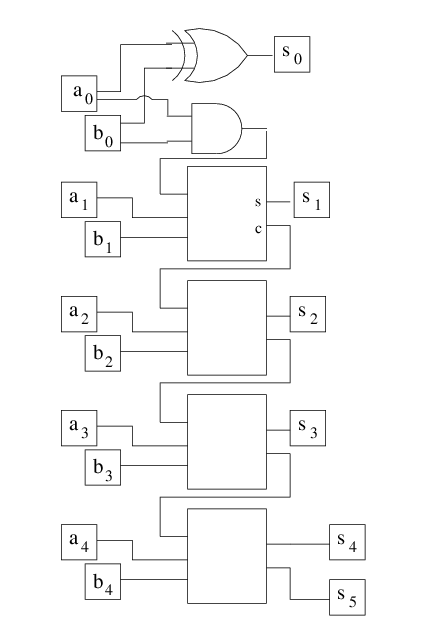
We can connect full adders to each other to form a ripple-carry adder.
Let's let a full adder be represented by this symbol:
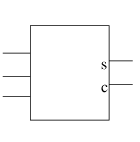
The 3 wires on the left lead from the inputs, and the wires on the right
lead from the outputs with the top output being the parity (or "sum") and
the bottom output being the majority (or "carry"). Then a 4-bit ripple
carry adder looks like this: