matrices

https://sparse.tamu.edu

Try the new SSGET interface for MATLAB and as a stand-alone Java application.

The new SSGET connects to sparse.tamu.edu instead of the UF site.

A matrix is sparse if it's mostly zero. Sparse matrices arise in many applications in science and engineering, and these applications dictate a very complex and elegant structure of where the nonzeros appear. So what does the structure of a mathematical equation look like? To answer that question, draw a dot on a page for each equation, and draw a line between two dots if the equations are related (dot 1 and dot 2 have a line if the (1,2) entry of the matrix is nonzero). What your picture looks like depends on where you draw the dots on the page, but the problem is the matrix doesn't tell you where to put the dots. To find out, give each dot an electrical charge, and make each line a spring. Drop the equations on the floor and let them wobble until they settle into a low-energy state, where everything is in balance. Then color the short lines red, the long ones blue, and the middle ones green. These are the images you see on display -- both mathematically illuminating and strikingly beautiful. The images below are created from the SuiteSparse Matrix Collection, by Yifan Hu of AT&T Research.

Sproing und Wobble: A Barrier Hessian Matrix from Convex Quadratic Programming (2009). Force-directed graph visualization places a positive electrical charge on each node and a spring on each edge and then computes a low-energy state for the graph, revealing the elegant structure of the mathematical relationships within this symmetric positive definite sparse matrix.

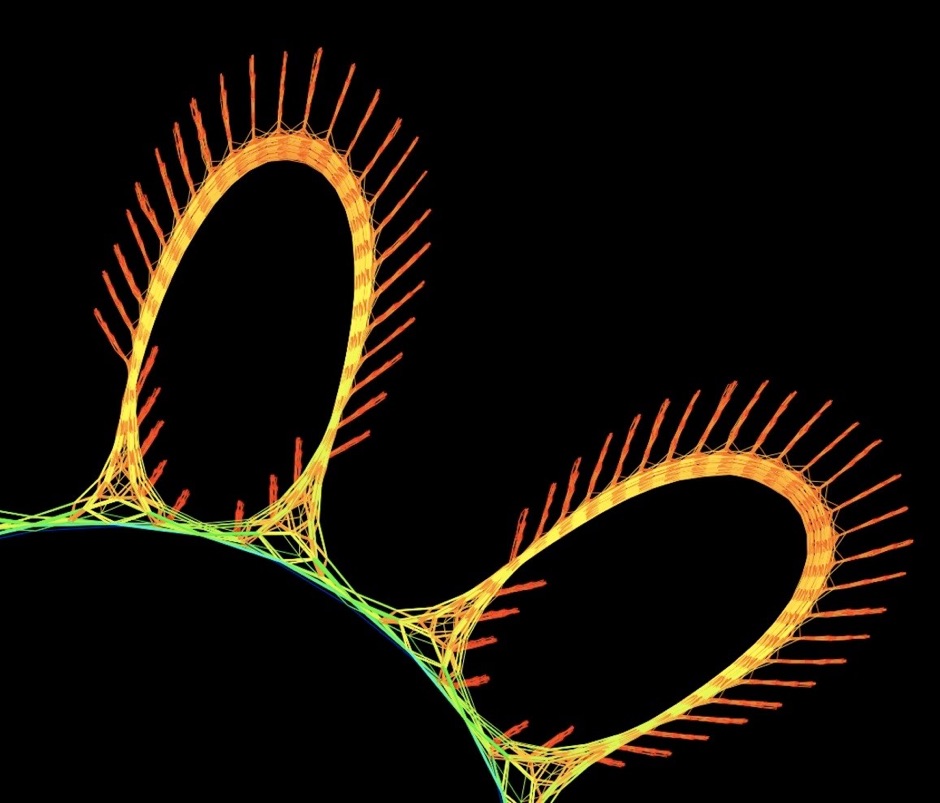
Daisy Chain: Financial Portfolio Optimization (2009). Optimizing a financial portfolio leads to a graph with many branches, each depicting a possible future economic scenario. Which path will your portfolio take?

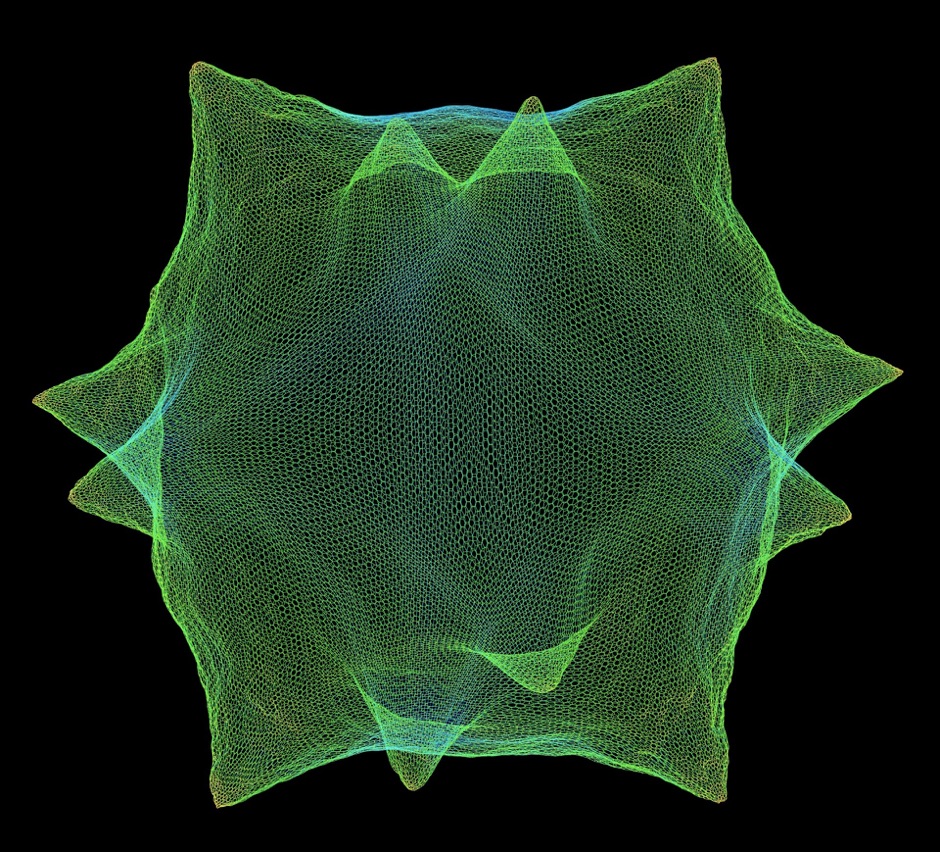
A Fishnet for Shallow Water Equations (2009) A computational fluid dynamics simulation of a shallow bay of water pretending to be a shimmering green fishnet.

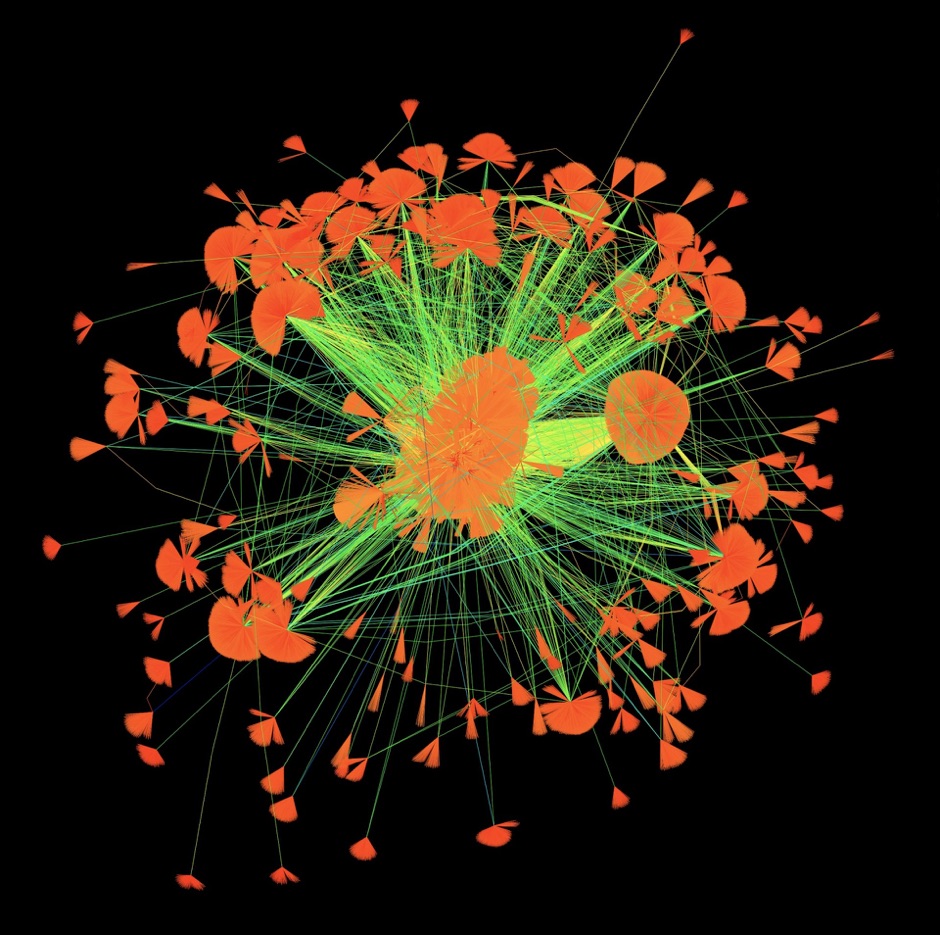
Web Poppies (2009) You like a web page and I like it too. 512 people like 394,792 web pages, do you like them too?

One Fish, Two Fish (2009) A blue constraint matrix from a linear programming problem meets a reddish-orange frequency-domain circuit simulation matrix constructed via the harmonic-balance method, swimming alongside.