Fault Tolerant Real-Time Connection Admission Control
for Mission Critical Applications over ATM-based Networks

B. Devalla	R. Bettati     W. Zhao
IP & ATM Network Planning	Department of Computer Science
Nortel Networks Systems Engineering	Texas A&M University
Richardson, TX	College Station, TX  77843-3112
bdevalla@nortelnetworks.com	{bettati,zhao}@cs.tamu.edu

Abstract

1  Introduction

Real-time communication is concerned with the problem of delivering messages by their deadlines. Such a communication service with delay guarantees is crucial for mission critical real-time applications. Fault tolerant real-time communication deals with delivery of messages by their deadlines even in the presence of faults. Mission critical applications in embedded systems (such as those in submarine, aircraft, or industrial process controllers) demand Quality of Service (QoS) guarantees in terms of bounded message transfer delays. These applications preferentially use connection-oriented services as they are well-suited for applications that demand performance guarantees [3]. A connection can be viewed as a contract between an application and the connection management system. A real-time connection is characterized by stringent deadline constraints imposed on its packet delivery time. Fault-tolerant real-time connections require that the messages be delivered within the deadlines even in the presence of faults. The defining characteristic of connection-oriented communication is the existence of a connection establishment phase preceding the actual data transfer. A critical part of connection management is the Connection Admission Control (CAC) procedure, which decides whether or not a connection can be admitted, based on the QoS requested and the resources available. We will concentrate on developing fault tolerant real-time connection management in this paper.

We design Fault Tolerant Connection Admission Control (FT CAC) algorithms that decide on whether a connection can be admitted or not depending on resources available, tightness of delay bounds, and the presence of faults. Two issues must be addressed in order to provide fault tolerant real-time communications: First, we have to devise mechanisms to tolerate faults. We also have to identify redundancy parameters necessary to support reliable delivery of messages within their deadlines. We consider an integrated approach to tolerate transient and permanent faults by combining space and temporal redundancy approaches. Second, a delay analysis methodology must be used compute the end-to-end delays suffered by connections in the worst case in order to guarantee message delivery by the deadline. We first develop a generic traffic model to describe the traffic of individual connections in the network and derive end-to-end delay bounds taking into account the impact of faults.

2  Previous Work

Network-centric approaches typically encompass network survivability and are more suited to networks that offer best-effort service like the Internet. Survivability of fiber networks is discussed in [10,13,22,23]. Self-healing networks are considered in [9]. Virtual Path (VP) routing and restoration is discussed in [1,14,20]. The techniques mentioned in this section are expensive and are used only in the network backbone. The host-centric approach is more suited to real-time communications. Typically a network manager element (either centralized or distributed among hosts) is present in real-time communications that guarantees the timeliness of messages. This manager now takes on the additional responsibility of ensuring reliable communications. The network manager is typically implemented as a middleware and resides between the applications and the operating system. Generic design principles on the integrated design of both fault tolerance and real-time constraints is discussed in [18,19,21]. The networks used can either be multiple-access LANs or point-to-point networks. Multiple access LANs used to support performance guarantees typically have the ring topology and FDDI is the most popular high speed network protocol. Integrated fault tolerant real-time communication has been addressed for in a variety of network settings in [2,4,8,11,16,17]. Han and Shin detail detect-and-recover approaches to fault tolerance by establishing D-connections (short for dependable real-time connection) in [7]. The D-connection consists of a primary channel and one or more backup channels. A backup channel remains a cold-standby until it is activated due to detection of faults. As with any detect and recover approach, data is lost during the time interval when the failure is handled.

Our work complements previous work in the area of fault tolerant real-time communications. We consider communications over ATM networks. The fault model includes transient and permanent faults. By using a proactive approach to mask the effects of faults, no data is lost as long as the faults are no more than the fault tolerance level requested a priori by the connection.

3  Models

Fault Model. We consider both transient and permanent faults. The difference is the length of duration of these faults and consequently how they affect the packets in a connection. The lifetime of a transient fault is small compared to the lifetime of a connection. In this work, we assume that a transient fault is temporary and affects at most one packet. A permanent fault occurs for a much longer duration and affects more than one packet.

Connection Model. A fault-tolerant connection management system relies heavily on appropriate connection specification, both in terms of connection QoS specification and fault requirements. The periodic model is traditionally used to specify the QoS of a connection. A connection is specified by the ordered triplet: (C,P,D), where C is the message size in bits generated periodically every P time units, and each message has a deadline D time units. Let d^msg be the worst-case delay suffered by the messages in the connection. The connection management system admits the connection only if there are enough resources to admit the connection such that d^msg £ D for the incoming and existing connections.

Additionally, a connection can also specify fault tolerance requirements. A connection is thus specified by the quintuplet: (C,P,D,X,Y) where X is the number of transient faults and Y is the number of permanent faults that the connection wants the connection management system to guard against. The fault specifications do not include the location of the fault nor do they include the time of occurrence or the status of the network. The contract between the real-time connection and the overseeing management system deems that if the connection is admitted then all the messages of the connection are guaranteed to be delivered within the deadline as long as the number of transient faults is no more than X and the number of the permanent faults is no more than Y.

4  Fault Tolerant Real-Time Connection Admission Control

We design fault tolerant connection admission control with a number of objectives in mind: First, it must provide delay guarantees in the presence of faults. Our goal is to ensure predictability and reliability. We allow for connection-level fault tolerance, where each connection specifies the fault tolerance necessary, rather than designing the entire system for a specific level of fault tolerance Next, we support dynamic connection arrivals. The connection arrival pattern is not known ahead of time. Connection admission decision is made each time a connection arrives and there is no restriction on when the connections can arrive. Proactive fault tolerance provides a priori guarantees at connection admission time. A further goal is the effective use of redundant resources to allow for high admission probability. Along with that, the CAC must be efficient, and respond promptly to connection requests. Finally, compatibility with existing platforms is important.

Traditionally, fault tolerance is achieved in one of the following two ways:

Spatial Redundancy: With this method, copies of a message are sent on redundant paths. Spatial redundancy is in terms of using redundant paths. A copy of a message is sent on redundant paths. The presence of redundant network elements ensure that there are redundant paths between communicating hosts. Spatial redundancy is the surest way to tolerate permanent faults. As long as at least one of the paths is functional, the message will be delivered. It is typical to provide redundant paths by multihoming hosts on multiple networks.

Temporal redundancy: With this method, copies of a message are retransmitted multiple times on the same path. This is very effective to overcome multiple transient faults. However, in real-time communications, time is a critical resource. The deadline requirements may not allow the luxury of multiple retransmissions.

Spatial redundancy utilizes the existence of redundant paths between communicating hosts and can effectively tolerate multiple permanent faults. However, this approach comes at a high cost, as it requires additional links and network elements. The temporal approach tries to use one path but redundant copies. This is an acceptable solution to tolerate transient faults provided the deadlines are not small. However, sending more than one copy on the same path does not increase the capability to tolerate permanent faults. Furthermore, temporal redundancy may not work well if the messages have short deadlines.

We use an integrated approach that combines both spatial and temporal redundancies. In the integrated approach, multiple copies of a message are sent on (multiple) redundant paths. The potential benefits lie in using the appropriate levels of spatial and temporal redundancies to tolerate permanent and transient faults. We inherit the advantages and disadvantages of each approach. We design the integrated scheme to exploit the benefits of effective fault tolerance and try to minimize the disadvantages. One may think of the integrated approach as a generic fault tolerance scheme with pure spatial and pure temporal approaches as being special cases. We present the details of our integrated approach in Section 5.

5  Integrated Fault Tolerant Connection Admission Control

Given an incoming connection admission request with the five parameters C,P,D,X,Y, the FT CAC has to make a series of decisions in order to test the admissibility of a connection.

Spatial redundancy requirement: We send copies of a message on several independent paths to tolerate faults. The degree of Spatial Redundancy, SR, of a connection is measured by the number of paths used and is bounded by:

Number of copies sent per path: We send multiple copies per path to tolerate transient faults. The number m of copies to be sent on each of the (Y + Z) paths is given by m = é(X+1)/Z ù. Once we find Z, we can directly compute the number of copies of the message to send.

Time interval between successive copies: The m copies on each path are sent D time units apart. We have to find D such that the worst case message delay, d^msg, is less than the corresponding deadline D for the new and existing connections. The effect of D varies depending on whether we are concerned about the new incoming connection or the existing connections. For the incoming connection, a smaller value of D implies better chances of meeting the deadline. However, a small value of D means more bursty traffic which has a detrimental effect on the delays of the existing connections.

5.1  Algorithms for the Selection of Spatial Redundancy

The choice of Z determines how much of spatial redundancy is used to tolerate faults. We will consider three different algorithms to select spatial redundancy, namely the Maximum, Minimum, and Adaptive Spatial Redundancy algorithms (MaxSR, MinSR, and ASR, respectively).

Maximum Spatial Redundancy Algorithm (MaxSR). this algorithm tries to provide fault tolerance using maximum spatial redundancy possible by choosing the largest value of Z allowed by available resources. Let Z^max be min(X+1,Q-Y), the maximum value of Z. The algorithm then selects a value for D, as described later. Once Z and D are selected, delay derivation gives the worst case delay. If the worst case delay is less than the deadline, we allocate resources and accept the connection. If, on the other hand, the worst case delay is greater than the deadline, the connection admission request is rejected. MaxSR tries to minimize load on the paths by selecting the maximum possible value for Z. Its execution time is low, due to its simplicity.

Minimum Spatial Redundancy Algorithm (MinSR). This algorithm tries to use as few paths as possible thus minimizing the spatial redundancy used to tolerate faults as follows: First, it checks to see if a new connection can be admitted when Z has the minimum value, Z^min of 1. If this test fails, MinSR tries to admit the connection with increasing values for Z, until either the connection is admitted, or Z reaches the maximum value Z^max. While this iteration increases the execution time of the algorithm, this is limited, as the numbers for Z is usually small (typically between 2 and 4). For larger values, binary search can be used. The use of Algorithm MinSR is to be preferred in cases where a minimum number of path should be used in order to keep more paths available for future arrivals.

Adaptive Spatial Redundancy Algorithm (ASR). We propose another algorithm with the express intent of increasing the likelihood of a connection being admitted. Since we use an integrated spatial and temporal approach, it is interesting to test connection admission when the different redundant paths carry a balanced load. One way to ensure that paths are equally loaded is to measure the variance of the load of the different paths. The smaller the variance, the more balanced the load on the paths are.

The first step is to use the MinSR and Algorithm MaxSR to determine Z^min and Z^max. If a range can be found, ASR searches for a Z Î [Z^min  Z^max] that results in the best load balance among the paths. We call this the Adaptive Spatial Redundancy algorithm because it selects Z dynamically to adjust (adapt) the fault tolerance to balance the load among the paths.

This load distribution affects the likelihood of admission of future connections. Note that if a connection is admitted, it adds load to (Y+Z) paths. With Z^min, fewer paths have this additional load but the load is unevenly distributed. It is possible that a future connection may need a smaller load but more paths. To admit a connection, the ASR algorithm first finds Z^min and Z^max at which a connection can be admitted.

5.2  Algorithm for the Selection of D

Recall that D is the time interval between successive copies of a message. The value of D is limited to D ³ D^min = T_pkt and D £ D^max = P/m. T_pkt is the minimum time taken to process a packet in an ATM network. The upper bound is due to the fact that the m copies are sent periodically apart by D while the messages have a period P. The m-th copy needs a chance to be delivered before the transmission of a copy of the next message.

For the incoming connection, a smaller value of D implies better chances of meeting the deadline. However, a small value of D means more bursty traffic which has a detrimental effect on the delays of the existing connections.

Fixed D Algorithm. Given the bounds of D, a simple choice is a fixed value, for example D = (D^min + D^max)/2. The traffic rate due to the copies is neither too high nor too low. Choosing a fixed value for D speeds up the execution time of the CAC algorithm.

Adaptive D Algorithm. A large value of D helps the existing connections while a smaller value may help the incoming connection. Thus, to help increase likelihood of a connection admission, the algorithm for selecting D can be made adaptive by selecting D iteratively from the range (D^min  D^max). The iteration starts with the initial value of D=D^max. If the connection cannot be admitted at D^max, we iterate until we find the largest possible value for D in the range (D^min  D^max). Iterating for D increases the likelihood of a connection being admitted because FT CAC now has a choice on the value of D. This method however increases the execution time of the algorithm.

5.3  Worst Case Delay Computation

All the FT CAC algorithms discussed in the previous section had a step called the computation of worst case delay. It is critical to be able to derive worst case delays suffered by messages. The connection admission control algorithm can admit a connection if the worst case delay suffered by the connection is less than its deadline.

The objective of delay computation is to derive the worst case value of the end-to-end delays of the messages in a connection. Let d^msg be the worst case end-to-end delay of messages of a connection. Recall that we send copies of a message on SR different paths to tolerate faults. Let d^copy_j be the worst case delay for a copy of a message of the connection along the j-th path (1 £ j £ SR). Depending on the load on the paths, d^copy_j is different on different paths. Let d^copy be the worst case delay of a copy of the message, that is, d^copy is the maximum among all d^copy_j's. Now, in the worst case, only the last (i.e. the m-th copy) reaches the destination. This thus gives the worst case message delay, d^msg.

In the following delay computations are based on the computation of local delays on the output ports of switches and routers. We treat these ports as multiplexor servers, and call them servers for short.

5.3.1  Traffic Functions

The local delay at each servers can be easily computed based on a description of the traffic arriving at that server. We use the traffic function F(I) to describe the worst-case amount of traffic (in bits) of a connection arriving at a server in the presence of faults over any time interval of length I. We first consider the traffic at the entry of the network. This gives the input traffic at the first server.

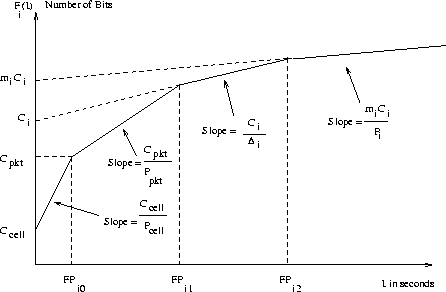
Let F_i(I) be the traffic function of the i-th connection. We note that the connection's traffic function can be approximated by a sequence of piecewise linear portions, that can be identified in turn as the cell-burst region, the packet-burst region, the region caused by multiple copies of a message, and the message region. One point for the approximation is given by measuring the cell length (C_cell) and the minimum distance between two consecutive cells (P_cell). Similarly, we also measure the packet length (C_pkt) in bits and the minimum distance between two consecutive packets (P_pkt) in time units, as the packets enter the network. This gives us the second point. The third point is given by the copies of the message each of size C_i bits sent D_i time units apart. m_i copies of the message sent every P_i time units gives the fourth point. We can therefore represent F_i(I) by a set of four linear portions, as depicted in Figure 1.

C_cell/P_cell is the LineSpeed of the network. For an OC3 ATM network, this is 155 Mbps. C_pkt/P_pkt was measured on a local ATM testbed by observing inter-packet distances, and we found it to be 42.87 Mbps. FP_i0, FP_i2, FP_i2 are called Flex Points. The slope of the line segments changes at each of these three flex points. This approximation is a relatively tight upper bound of the actual traffic in the network and helps in closed form computation of end-to-end delays of messages. For further details on the derivation of this traffic function please refer [6].

F_i(I) described thus far gives the input traffic at the first server (say Fⁱⁿ_i(I)). Using this input traffic function, we will derive the worst case delay at the server in Section 5.3.2. Let the worst case local message delay at the first server be d. We thus have the input traffic and the delay at the first server. The input traffic at the second server is nothing but the output traffic, F^out_i(I), of the first server. It is well known from previous work ([5]) that

5.3.2  Delay Computation

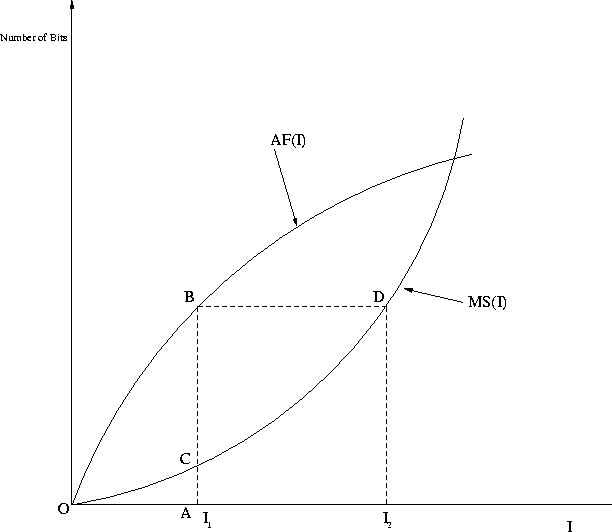
We now discuss how to derive worst case delays using the traffic function and the scheduling discipline at a server. In general, more than one connection can be passing through a server. Based on the scheduling discipline, the connections can be grouped according to the service priorities. We use the aggregate traffic function AF(I) as our traffic descriptor. Let AF(I) be the aggregate traffic function of a group of N connections multiplexed at a server.

For a given pair of AF(I) and MS(I), we can derive the worst case delay for a group of connections as illustrated in Figure 2: In an interval of length I₁, AF(I₁) = AB represents the maximum number of bits of a group of connections that can arrive at the server, and MS(I₁) = AC represents the minimum number of bits that can be served for the group. So AF(I₁)-MS(I₁) = BC represents the worst case queue length at the server in an interval of length I₁. The delay suffered by the bit is given by BD. Hence, the worst-case delay d^msg is given by:

The basic principles of delay analysis presented above are similar to that in  [12,15]. However, the derivation of delays in this paper is different from the previous work. We consider copies of a message and derive the worst case message delay from the worst case delays of the copies. Second and more importantly, the traffic function used in our work includes the effect of fault tolerance mechanism by accounting for the multiple copies of C_i bits sent D_i units apart in addition to the message itself being periodic.

6  Performance Evaluation

In this section, we discuss the evaluation of our fault tolerant connection admission control (FT CAC) algorithms by discrete event simulation. We consider a fault tolerant ATM switched network that provides 5 redundant paths between any pair of hosts. The link speed is 155 Mbps. Connection requests arrive at random with an exponential inter-arrival rate. We consider messages with an average C of 20,000 bits arriving periodically every 20 ms and having deadlines of 20ms. The connections also specify their fault requirements in terms of transient faults, X and permanent faults Y. X and Y are uniformly sampled from the ranges (0,1,2,3,4,5,6) and (0,1,2,3), respectively. The network itself is liable to experience faults. All links are equally likely to be faulty. FT CAC thus makes admission decisions based on both the requirements of a connection and existence of non-faulty paths. We have evaluated the performance of the FT CAC algorithms for other data sets in  [6]. The data presented here is representative of the performance.

In order to determine the effectiveness and the efficiency of the FT CAC algorithm, we measure Admission Probability (AP) and Average execution time (AET), respectively. The former is the ratio of accepted connections over the total number of connections requesting admission, while the average execution time is the amount of time an application has to wait to get a reply from FT CAC algorithm after submitting a connection admission request.

6.1  Performance Comparison of Fault Tolerance Approaches

We compare the performance of our integrated approach to pure spatial and pure temporal approaches. We choose Algorithm MaxSR for the selection of spatial redundancy with D selected adaptively as our candidate Integrated Approach (IA). Algorithm MaxSR is simple to implement and as will be seen from the next section, performs close to the more complex Algorithm ASR. To highlight the comparison, the connections require tolerance exclusively against transient faults (i.e., (Y = 0)). We thus compare how well the IA compares with a pure Spatial Approach (SA) and pure Temporal Approach (TA) as the number of transient faults to tolerate changes. If a connection demands a tolerance to X transient faults, SA uses X+1 paths, and TA transmits X+1 copies.

 
(a)  Admission Probability

 
(b)  Average Execution Time

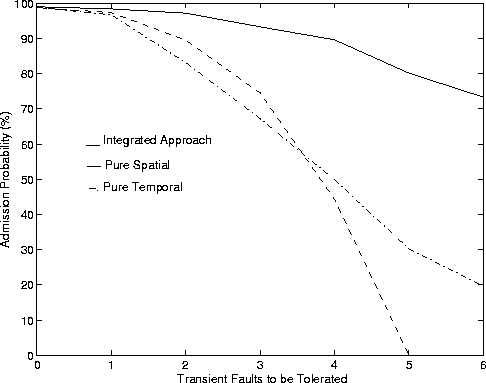
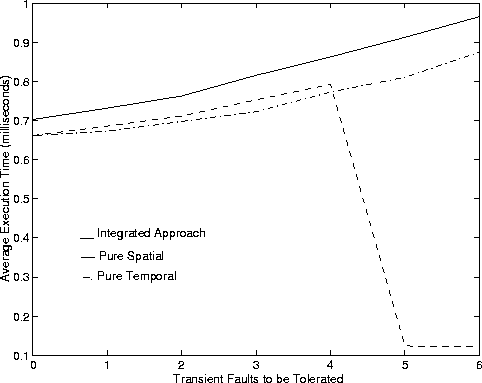
Figure 3 shows AP and AET of the three approaches plotted against the number of transient faults to be tolerated. We make the following inferences:

 
(a)  Admission Probability

 
(b)  Average Execution Time

 
(a)  Admission Probabiliy

 
(b)  Average Execution Time

First, the integrated approach performs far better than the pure spatial or pure temporal redundancy approaches. This is to be expected as the integrated approach tries to use a judicious mix of spatial and temporal redundancies for fault tolerance.

Second, when the number of transient faults to be tolerated is smaller, the spatial approach can find alternate paths rather easily and so it performs better than the temporal approach. As the number of transient faults is large (say 5 or more), the spatial approach tries to find (X+1 > 5) paths between communicating hosts. Since only a maximum of 5 is allowed by the configuration, it rejects all connections and hence, AP is zero. The temporal approach has a lower (but non-zero) AP for a larger number of transient faults because it tries to send multiple copies to satisfy the fault requirements of the incoming connection.

Finally, we do pay a price for using a more complex algorithm as the AET is more for the integrated scheme. The temporal approach is the quickest because it only has to select the value of the number of copies. The spatial approach takes more time than the temporal approach because of the time taken to select the multiple paths. The integrated approach takes more time because it takes more iterations of selecting redundancy configuration to try to accept more connections.

6.2  Performance Comparison of Algorithms to Select Redundancy Parameters

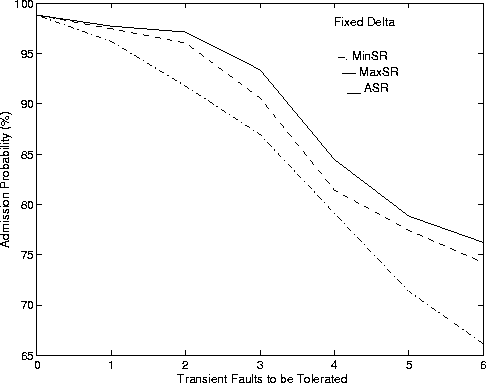
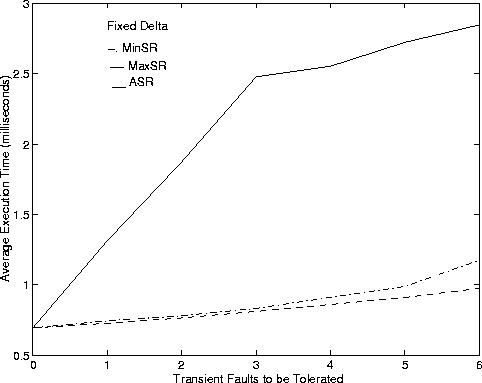
We evaluate the performance of the FT CAC algorithm for different choices of the redundancy parameters detailed in Section 5. We first show performance of algorithms by using a fixed value for D = (D_min + D_max)/2. Recall that Algorithm MinSR tries to choose a minimum value for Z while Algorithm MaxSR tries to choose the maximum value for Z. Algorithm ASR tries to keep the load balanced on all the paths. Figure 4 shows admission probability and average execution time against the number of transient faults to be tolerated.

Algorithm ASR has a better AP than the other two algorithms. This is to be expected. ASR tries to keep variance of the load among the paths to a minimum. This helps increase the likelihood of admission for future connections. Note that Algorithm MaxSR's performance compares well with that of Algorithm ASR. When the number of transient faults is no more than three, the AP reduces only by a small margin. When the number of transient faults is 4, the drop in AP is due to the manner in which fault tolerance is handled. Algorithm MaxSR, may be forced to send a second copy of the message to tolerate the larger number of transient faults. The AP of Algorithm MinSR drops as the number of transient faults increases. This is because more copies are used to ward off transient faults, which in turn increases the load on the network.

The AET reveals the penalty paid in using the highly iterative Algorithm ASR. Algorithm ASR iterates on to find the best value of Z that keeps load balanced in the network and this increases the average execution time. Algorithm MaxSR has the lowest average execution time because it tries to admit connections at just one value of Z. Algorithm MinSR has slightly larger AET as the algorithm iterates until it finds the smallest Z to admit a connection.

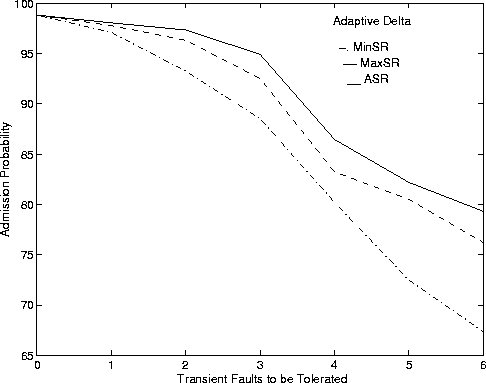
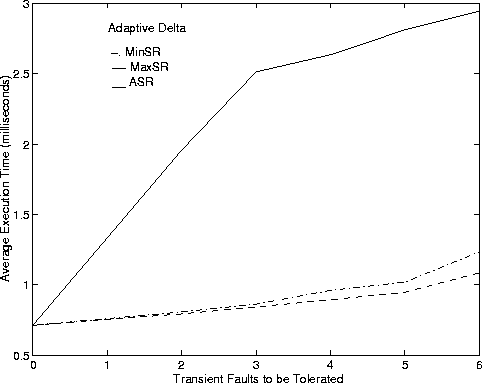
Figure 5 shows admission probability and average execution time against the number of transient faults when using the adaptive D algorithm. The APs with adaptive D are higher than the corresponding data with a fixed value of D. In addition, while the AET is higher with iterative D, the difference is not much (less than 0.1 milliseconds). The highest AET for Algorithm MaxSR is less than 1.5 milliseconds, a number considered very acceptable to get a response from the FT CAC algorithm.

From the results presented, it is clear that it is beneficial to use an integrated approach rather than a pure spatial or a pure temporal approach. The data from performance figures do not allow us to draw a conclusion that easily. We qualitatively classify the performance of the FT CAC algorithms in Table 1.

7  Conclusion

This paper presented a design FT CAC algorithms that admit connections with real-time and fault tolerance requirements contingent on resource availability. The main contributions of this research are as follows: We designed fault tolerant real-time connection admission control. Connections specify real-time and fault tolerance requirements and the connection admission control mechanism decides whether a connection can be admitted or not based on the resources available. The fault tolerance mechanism integrated both spatial and temporal redundancies. We discussed the computation of end-to-end delays of messages due to the fault tolerance mechanism. The path of a connection traverses multiple servers. A traffic function used to describe the worst case traffic at the input of a server was specified. The input traffic function and the scheduling discipline at the server are used to derive the worst case delays suffered by a message at the server and the output traffic from the server. We provided a methodology to derive end-to-end delays.

We evaluated the performance of fault tolerant real-time connection admission control procedure and showed that our approach, which integrates time and space redundancies, performs significantly better than either pure spatial or pure temporal approaches.

Our design is compatible with existing network technologies and can be implemented at user level without modification to the operating system kernel or network protocols. The methods proposed do not require proprietary hardware nor do they necessitate any changes to the system software.

References

[1]

J. Anderson, B. Doshi, S. Dravida, and P. Harshavadhana. Fast Restoration of ATM networks. IEEE Journal on Selected Areas in Communications, 12, Jan 1994.

[2]

Anindo Banerjea. Fault management for realtime networks. Technical Report UCB//CSD-95-861, EECS Computer Science Division, University of California, Berkeley, December 1995.

[3]

B.Devalla, C. Li, A. Sahoo, and W. Zhao. Connection oriented real-time communication for mission critical applications. In Proceedings of IEEE NAECON, pages 698-707, 1998.

[4]

B. Chen, S. Kamat, and W. Zhao. Fault-Tolerant Real-Time Communication in FDDI-based Networks. IEEE Computer, pages 83-90, April 1997.

[5]

Rene L. Cruz. A calculus for network delay, part II: Network analysis. IEEE Transactions on Information Theory, 37(1):132-141, January 1991.

[6]

B. Devalla. Fault Tolerant Real-Time Communications over ATM Networks. PhD thesis, Texas A&M University, College Station, Texas., 1999.

[7]

S. Han and K.G. Shin. A Primary-Backup Channel Approach to Dependable Real-Time Communication in Multi-hop Networks. IEEE Transactions on Computers, 47:46-61, Jan 1998.

[8]

S. Kamat and W. Zhao. An FDDI-based reconfigurable network for fault-tolerant real-time communications . In Proceedings of the Fault-Tolerant Parallel and Distributed Systems, pages 188-99, 1995.

[9]

R. Kawamura, K. Sato, and I. Tokizawa. Self-healing ATM networks based on Virtual Path Concept. IEEE Journal on Selected Areas in Communications, 12, Jan 1994.

[10]

R.J. Kochanski and J.L.Paige. Safenet: the standard and its application. In Proceedings of IEEE-LCS, pages 46-51, 1991.

[11]

H. Kopetz and G. Grunsteidl. TTP-a protocol for fault-tolerant real-time systems. Computer, pages 14-23, January 1994.

[12]

C. Li, R. Bettati, and W. Zhao. Static Priority Scheduling for ATM Networks. In Proc. of RTSS. IEEE, 1997.

[13]

K. Murakami. Survivable Network Management for High-Speed ATM Networks. PhD thesis, Carnegie-Mellon University, Pittsburgh, Pennsylvania, 1995.

[14]

K. Murakami and H.S. Kim. Virtual Path Routing for Survivable ATM Networks. IEEE/ACM Transactions on Networking, 4:22-39, Feb 1995.

[15]

H. Sariowan and R.L. Cruz. A Service-Curve Approach to Performance Guarantees in Integrated-Service Networks. In Proc. of the ICCCN. IEEE, 1995.

[16]

S. Schultze. Fault-tolerance in real-time communication. In Proceedings of the IEEE International Symposium on Industrial Electronics, pages 583-7, 1993.

[17]

K.G. Shin, L.-H.Ng, and T.P. Monaghan. A layered approach to fault-tolerance and timeliness issues in safenet. In Proceedings of Local Computer Networks, pages 146-155, 1994.

[18]

K.G. Shin and P. Ramanathan. Real-time computing: a new discipline of computer science and engineering. In Proceedings of the IEEE, pages 6-24, 1994.

[19]

John A. Stankovic. The integration of scheduling and fault tolerance in real-time systems. Technical Report COINS TR 92-49, University of Massachusetts, March 1992.

[20]

Technical Committee. PNNI Specification Version 1.0. The ATM Forum, 1996.

[21]

F. Wang, K. Ramamritham, and J.A. Stankovic. Determining Redundancy Levels for Fault Tolerant Real-Time Systems . IEEE Transactions on Computers, pages 292-301, February 1995.

[22]

T-H Wu and N. Yoshikai. ATM Transport and Network Integrity. Academic Press, 1998.

[23]

T.H. Wu. Emerging Technologies for fiber network survivability . IEEE Communications Magazine, Feb 1995.