Abstract
Large-scale distributed real-time systems are increasingly difficult to analyze within the Rate Monotonic Analysis framework. This is due partly to their heterogeneity, complex interaction between components, and variety of scheduling and queuing policies present in the system. In this paper we present a methodology to extend the traditional RMA approach by allowing general characterization of workload and flexible modeling of resources. We realize our approaches within ProtEx, a toolkit for the prototyping and schedulability analysis of distributed real-time systems. This toolkit focuses on a wider set of methodologies than the traditional RMA scheduling analysis tools.
Key words: Distributed Real-Time Systems, Schedulability Analysis, Prototyping
Unfortunately, the development of analysis methodologies to support the design and the verification of these emerging systems has not kept pace. The current technologies are mostly based on the Rate Monotonic Analysis (RMA) methodology. While RMA-based methods have proven to be effective for the analysis and verification of smaller systems, a number of shortcomings limit their usefulness for larger systems. We elaborate on three of them:
First, traditional design and analysis methodologies lack an integrated model for computation and communication. Practical considerations have traditionally led to very different ways of analyzing real-time computation and real-time communication. For example, the comparatively small granularity of units of workload in networks allows for round-robin-style scheduling (such as fair queuing and variations thereof) in switches and routers. These classes of schedulers are less appropriate in computation nodes because units of computation are rather large. Similarly, network elements, such as switches and routers, exhibit little or no blocking. Semaphores and other synchronization mechanisms in the endsystems can cause complicated blocking behavior with ensuing priority inversions. This artificial separation of computation and communication is awkward (for example, it leads to lower utilization,) and becomes more so as the boundary between the two becomes more fuzzy, as sophisticated communication primitives, for example reliable group communication, evolve.
Second, traditional design and analysis methodologies rely heavily on workload regulation. Formulas for delay computation make assumptions about worst-case workload; typically they assume periodic workloads. Various forms of regulators make sure that these assumptions are satisfied. For example, rate controllers in packet schedulers (e.g. [16]) enforce a minimum inter-arrival time of packets. Similarly, various forms of sporadic servers ensure that non-periodic real-time workload is executed in a controlled fashion (e.g., [9]). As another example, resource access protocols based on priority inheritance or priority ceiling [15] control the eligibility for execution of the critical sections by appropriately modifying the task's priority. The pervasive use of regulation is problematic for the class of systems described above, as it adds run-time overhead and very poorly handles integration of COTS components and hardware and software composition in general 2.
Third, traditional analysis methodologies make simplistic assumptions about resources. Active resources, such as CPUs or communication links, are typically modeled as constant-rate servers. In real systems, the rate at which jobs can be served is highly variable. Lower-level operating system layers, for example, add various forms of hidden scheduling and priority inversion [13,14]. Simply assuming a worst-case rate for active resources is a common technique, which unduly reduces resource utilization. Rather, resources must be modeled in a way that allows to flexibly describe the worst-case availability to particular jobs.
Over the last few years our group has developed a number of workload modeling techniques to analyze systems with widely varying workloads [6]. At the same time, we have investigated the applicability of service functions for the general modeling of communication and computation servers [4]. The result of these investigations became a set of techniques that can be used, possibly in conjunction with traditional RMA, to analyze large-scale heterogeneous systems that consist of a wide variety of workloads and servers. It also became apparent that some of these techniques (such as service-function based [12] or integration-based [5]) for end-to-end analysis are superior, to our knowledge, to all currently used methods.
We integrated these techniques into ProtEx, a toolkit for analysis of distributed real-time systems. ProtEx is a toolkit used for prototyping and performing schedulability analysis of distributed real-time system and is well adapted for a networking environment. The ProtEx toolkit is comprised of a set of resource, workload, schedulability analysis and user interface software modules. It gives the possibility to the user to design, prototype, and analyze a system with varying resource and workload characteristics. ProtEx is used during the design phase of a project. A number of workload characterization and delay analysis techniques developed by the Texas A&M Real-Time Research Group and by others are integrated in the ProtEx toolkit [4,5,6].
ProtEx performs end-to-end or individual schedulability analysis for a defined set of tasks based on a selected analysis methodology. It provides the user with the ability to incrementally work on an application prototype before going into the implementation, testing, and integration phases of the software life cycle. By performing extensive schedulability analysis during the design and prototyping phase, ProtEx can ultimately save time during the next phases of the application development.
In this paper we will first motivate the need for general workload characterization and for flexible resource modeling for end-to-end analysis of distributed real-time systems in Section 2. In the following sections we will describe the design of ProtEx. The structure of the toolkit is rather canonical, as it consists of modules for workload characterization, resource description, and analysis. In Section 3 we describe the modeling of the system resources and workload by decomposition into server graphs and task graphs. We also describe the schedulability analysis techniques used for single node and end-to-end analysis. A large number of schedulability analysis tools, most of them based on RMA, are available. We shortly describe two of them in Section 4. The overall design of ProtEx is described in Section 5 and we conclude in Section 6.
In order to meet the requirements for analysis methods for real-time systems, novel forms of modeling resources and workload must be used. In this section, we propose such methods, based on general characterizations of workload and flexible resource modeling.
Traditionally, work on schedulability analysis in endsystems focuses on periodic jobs, where the inter-arrival time of requests is fixed to be the period of the job. Non-periodic workload is typically transformed into periodic workload by either one of the following three ways: (i) by treating the non-periodic jobs as periodic jobs with the minimum inter-arrival time being the period, (ii) having server, which look like periodic jobs to the rest of the system, execute the non-periodic jobs (e.g. [9]), or (iii) splitting the non-periodic jobs each into collections of periodic jobs of different sizes and periods. In all three cases, well-known schedulability analysis methodologies for periodic workloads can be used.
Applying the same methodologies for distributed real-time systems, where jobs execute across multiple end-systems, shows poor results, even for periodic workloads. While the arrival of instances of a periodic job may indeed be periodic at the first processor, the completion of these instances almost certainly is not. If no special action is taken, and the completion of an instance indicates that the second processor can go ahead, the ärrival" of instances of the jobs on the second processor is not periodic.
By appropriately synchronizing, or regulating, the execution of the jobs on the processors, excessive bursts can be eliminated, which increases schedulability, and the job execution can be made to adhere to simple workload descriptors, which makes rigorous schedulability analysis possible. A number of such synchronization schemes were presented in [10]. They allow the use of traditional schedulability analysis methods for periodic workloads.
It is well known that appropriate regulation reduces the worst-case end-to-end response times as compared to systems without regulation. However, regulation adds overhead to the system and increases the average end-to-end response time for jobs. In addition, it is of limited applicability when the workload is inherently aperiodic.
Finally, not all components in the system may be accessible enough to allow for integrated regulation. Wrappers would then have to be realized, which may unduly increase overhead.
To deal with systems that have limited or no support for workload regulation, we use workload characterization: instead of regulating the workload after each processor to conform to a predetermined descriptor, we use general descriptors and compute the descriptor of the workload after each processor. The methods for this depend on the scheduling policies and the other workload present on the processor. Our group has applied these techniques in various forms at network level, and we are using some of these within ProtEx for the analysis of systems with both network and endsystem elements.
It is important to note that we do not envision workload re-characterization as a replacement for regulation. Rather, it is complementary and can be naturally combined with it, allowing for an integrated analysis methodology.
A model for processors must reflect that resources are not ideal. (i) Service to particular jobs may be interrupted or delayed because of various forms of priority inversion. (ii) Processors may be controlled by a variety of different scheduling policies. (iii) A modeling methodology must lend itself to effectively and accurately model hierarchical compositions of processors, be this a collection of processors, or processors in combination with operating system layers incorporating resource managers, or processors controlled by multi-level schedulers.
To achieve this, we make available a rich variety of different server types. In addition, we generalize the concept of service rate, which is traditionally used in processor modeling. Instead, we allow processors to be modeled by service functions, a well-known method to model service to traffic streams in networks [12]. As described later, service functions give a deterministic description of the worst-case processor availability to a particular job.
In addition, we take advantage of the flexible workload modeling described above as a means to compose systems with multiple different server types.
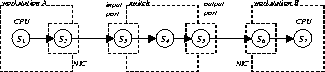
For analysis purposes, the system is decomposed into its basic resource components, which we call servers. Some servers can be mapped onto real hardware components (such as CPU, I/O ports, busses,) while others are logical in nature (such as workload regulators or servers for critical sections). We describe the collections of resources in form of a server graph, whose m nodes represent the available servers S1, S2, ¼, Sm, and the edges describe the connectivity among servers.

Figure 1 depicts a possible representation of a server graph of two workstations connected by an ATM switch. In this example, we model the ATM switch as a collection of input ports (S3), the switch fabric (S4), and a collection of output ports (S5). Each worksthation is described by a server representing the CPU and possible memory management and DMA machinery to the network interface card (S1 and S7) and one server representing the network interface card and the link to the ATM switch (S2 and S6).
We distinguish three classes of servers, depending on how they affect the analysis:
Similarly to previous prototyping and analysis tools, we model the workload, independently of whether it is computation workload in the end systems or routers, or traffic in the network, as a set of n tasks T1, T2, ¼, Tn. Each task Ti consists of a (typically infinite) sequence of invocations, called jobs, denoted by Ti(1), Ti(2), ¼, Ti(k), ¼ 3. Each invocation of Ti executes in sequence on one or more servers, and we call the portion j of each invocation k the subjob Ti,j(k). All invocations of portion j of Task Ti form the subtask Ti,j. We say that Ti,j executes on Server Si,j. Each subtask has a worst-case execution time of ei,j time units, meaning that each invocation executes for no more than ei,j time units on Si,j.
SERVERGRAPH sgexample: # Two workstations connected using a single switch
# Definition of component classes
CLASS SERVERGRAPH workstation # Definition of the workstation component
SERVER cpu:
TYPE = VARIABLE; POLICY = static_priority; # other parameters...
END;
SERVER network_interface_card:
TYPE =CONSTANT; # other parameters...
END;
# Definition of the connectivity within the workstation
cpu -> network_interface_card;
network_interface_card -> port1
END;
CLASS SERVERGRAPH ATMswitch # Definition of the ATM switch component
SERVER input_port:
TYPE = CONSTANT; # other parameters...
END;
SERVER switch_fabric:
TYPE =CONSTANT; # other parameters...
END;
SERVER output_port:
TYPE =VARIABLE; POLICY = FIFO; # other parameters...
END;
# Definition of the connectivity within the switch fabric
port1 -> input_port; input_port -> switch_fabric;
switch_fabric -> output_port; output_port -> port2;
END;
# Definition of the instances
SERVER wsA, wsB OF CLASS workstation;
SERVER switch OF CLASS ATMswitch;
# Definition of connectivity for the server graph using ports
wsA.port1 -> switch.portIN; switch.portOUT -> wsB.port1;
An invocation of task Ti on a server can spawn one or more invocations on one or more subsequent servers. Subjobs belonging to the same invocation are therefore in a dependency relation to each other that can be represented by a directed graph, which we call the task graph Gi for a given Task Ti. For simplicity of notation, we will limit ourselves to the discussion of task graphs that form chains of subtasks, and denote the first subtask as Ti,1, and an invocation of Ti,j+1 starting on its server only after the same invocation for Ti,j is finished on the previous server.
In order to allow for specification of non-periodic tasks and for uniform description of arrivals of tasks to servers in the system, we generalize the traditional periodic workload model by using arrival functions. The arrival function Fi,j,ARR(t) of subjob Ti,j is defined as the maximum number of invocations of Ti,j released during any interval of length t. A strictly periodic task arrival would therefore be represented by the arrival function
|
A number of different methods can be used to analyze the overall system, and the designer can pick the most appropriate method depending on the types of servers in the system and the system topology. All method rely explicitly or implicitly on the same approaches to analyze single-server systems. These approaches are then expanded to allow the analysis of end-to-end systems.
A number of delay formulas exist for workload that is defined by general arrival functions for a number of servers types. In its most general form, the delay dk,j for task Tk on Server Sj is given by the following formula:
|
|
In order to use these general formulas, the service function must be derived for each server type. Such service functions exist for FIFO and Preemptive Static-Priority Servers. Approximations exist for Non-Preemptive Static-Priority Servers [4]. For the various realizations of Generalized Processor Sharing Servers, the derivation of these functions is straightforward.
We note at this point that the use of these elaborate formulas is only necessary when the task arrival is bounded by a general arrival function. When tasks can be modeled as periodic, for example (this can be the case for periodic tasks at the first server, or just after a regulator server, or when the task arrival is conservatively modeled with a shorter period in order to take burstinness into account,) traditional time-demand analysis can be used to determine the local delay at a server.
The simplest form of end-to-end analysis partitions the system into isolated servers, computes the local delay on each server, and then computes the end-to-end delay by summing up all local delays along the critical path of a task. This method is called decomposition-based analysis, and has been first described in [11].
In order to compute the local delays at a server, the arrival functions for all tasks at that server must be known. These arrival functions are identical to the departure functions on the previous servers. Decomposition-based analysis can therefore be easily performed after the servers have been topologically ordered as defined by the task graph. If the task graph should contain cycles, this can be easily taken care of by using an iterative approach that terminates whenever the solution converges or when a deadline is missed.
Decomposition-based analysis is simple and suitable for systems with arbitrary topologies and server types. The drawback of this method is that it tends to overestimate the end-to-end delay suffered by the traffic. This is because it assumes that a task suffers the worst-case delay at every server along its connection path [5].
Better methods exist for special cases of workloads and servers. If service functions for all servers in the system exist, servers can be clustered by convoluting the service functions of the individual servers to generate service functions of aggregated servers [12]. The end-to-end analysis is then performed by performing a single-server analysis on the aggregated server. We call this method for ent-to-end analysis the Service Curve method.
Servers can be aggregated in special cases even when no service functions are provided. The Integrated Analysis method described in [5] aggregates pairs of FIFO or Static-Priority servers, and can be used to significantly improve the performance of decomposition-based analysis.
Schedulability analysis tools are typically used during the design phase to check and validate that these timing requirements are correctly enforced by the application. The core element of every schedulability analysis methodology is the processing and computation of the worst- case response times of the tasks defined in the system. After the calculation of the worst-case response time or delay, the calculated value is compared with the task's timing requirements.
Many prototyping and schedulability analysis tools in the domain of distributed real-time system have been and are currently developed in the industry and universities. We elaborate on two: Tri-Pacific offers a product suite of tools that include Rapid Rma, Rapid Sim, and Rapid Build [7]. This toolkit is based on research conducted at the University of Illinois at Urbana-Champaign [17], and uses a RMA approach. It allows the designers to test, simulate, and execute software models against various design scenarios and evaluate how different implementations might optimize the performance of a system.
TimeSys' TimeWiz [8] is another schedulability analysis tool that allows the user to build prototypes and validate them before implementation by analyzing and simulating the timing behavior of the system. This tool can analyze real-time applications to be run on network elements. As for TriPacific's toolkit, TimeWiz is based on the Rate Monotonic Analysis.
The main strength of these tools is that they provide convenient mechanisms for integrating and using multiple different tool characteristics, such as workload extraction and analysis into one single development environment. These tools also offer support for end-to-end analysis and simulation. However, they focus on a single schedulability analysis methodology approach, namely Rate Monotonic Analysis.
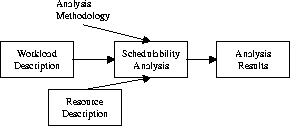
The ProtEx toolkit is divided into four separate modules, as described in Figure 3. The first module is the resource module, which provides the system definitions to be loaded and stored for analysis. The workload module, provides the task definition attributes to be executed on the defined resources. The third module is the schedulability analyzer, which performs the analysis based on the defined workload and resources, and selected methodology. Finally, the user interface module interacts and allows the user to define the resource and workload.
One of the core criteria of the tool is that the analyCalling ghostscript to convert, please wait ... Calling ghostscript to convert, please wait ... sis framework of ProtEx should be flexible. This feature allows the real-time software designer to select different types of methodologies when performing a schedulability analysis of the given resource and workload definitions. The user has the option to select three different types of methodologies. They consist of the decomposition-based, integrated-based and service curve-based analysis, along with the option of having discrete (for processor tasks, e.g.) or continuous (for network traffic) workload representation [5].
Another core criterion in the design of the ProtEx toolkit is to allow for modular resource and workload definition. Varying types of workloads can be modeled, and can be then executed on a variety of resource types. An additional criterion is to allow the designer to use and change different workload and resource characteristics during the prototyping phase of the application. This allows to determine any system bottlenecks and constraints early on in the software development life cycle. It also ensures a higher degree of flexibility when designing and analyzing an application.
The toolkit provides the ability to the user to define resources and workload in a fully hierarchical fashion. In fact, there is no real software limit on the level of hierarchy available. These resource and workload definitions are modular and adaptable since they can be changed at any time by the user. Except for the basic type of servers, no hard-coded resources are used by the schedulability analyzer. User defined resource and workload classes can be collected into libraries, and so give the user convenient access to high-level pre-defined components. This ensures extensive flexibility and modularity by having widely different components, servers, tasks and task types but still being able to perform a complete and precise real-time system schedulability analysis.
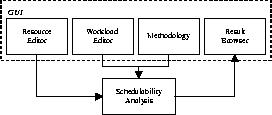
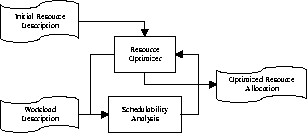
The ProtEx framework also defines a distinct separation or software de-coupling between the front end of the tool, i.e. the user interface and the back-end of the tool which handles the schedulability analysis and results. A clearly defined de-coupling scheme allows for easy integration of ProtEx with other tools. Figure 4 illustrates two possible uses of ProtEx: Figure 4(a) shows the standard configuration as stand-alone tool, with resource and workload specification done through editors, and the analysis being visualized by a browser. In Figure 4(b), ProtEx is integrated with other tools. Both workload and resource definition is generated by external tools, and a scripting environment drives ProtEx to optimize a set of resource parameters in this example. The loose coupling of the various ProtEx components also ensures smooth release upgrades of the toolkit
The initial ProtEx toolkit version has been developed to establish an infrastructure for large scale distributed real-time system prototyping and analysis. Resource and workload definitions with general characterization is a central aspect of the tool. The real-time software designer can use varying workload representation through service and arrival curves and specific schedulability analysis methodologies.
Through theoretical evaluations and results in [4,5], we have shown that this type of delay computation along with an appropriate methodology such as decomposition-based or integrated-based analysis generates better results for the schedulability analysis in terms of worst-case execution time and system utilization. Additionally, we have also built a framework that allows the user to hierarchically define and use resources and tasks for a given real-time application. Through clearly defined software module de-coupling, our tool is scalable for large scale distributed real-time system analysis.
1 Contact Information: R. Bettati, Department of Computer Science, Texas A&M University, H.R. Bright Building, College Station, TX 77843-3112, USA. Email: bettati@cs.tamu.edu, Phone: +1 (979) 845-5469, fax: +1 (979) 847-8578.
2 Whether the overhead is real or not is not relevant. The Mars Pathfinder Incident [18] is a well-publicized example where appropriate regulation in form of priority inheritance at a mutex was omitted because of perceived overhead.
3 In the following we will omit the invocation index (k) if it is not needed to distinguish individual invocations.