Providing Absolute Differentiated Services for Real-Time Applications in Static Priority Scheduling Networks
Shengquan Wang, Dong Xuan, Riccardo Bettati, and Wei Zhao1
Abstract
In this paper, we propose and analyze a methodology for providing absolute
differentiated services for real-time applications in networks that use
static priority scheduler.
We extend the previous work on the worst case delay analysis and develop a
method that can
be used to derive delay bound without specific information on flow population.
With this new method,
we are able to successfully employ Utilization-based Admission Control
(UBAC) approach
in flow admission. The UBAC does not require explicit delay computation at
admission time
and hence is scalable to large systems.
We also design and analyze several priority assignment algorithms, and
investigate their capability
of achieving higher utilization bounds. Traditional method of priority
assignment in this
domain has been one-to-one: all the flows in one class are assigned to one
priority. We find that
our newly designed algorithm many-to-many outperforms the one-to-one
algorithm significantly.
absolute differentiated services, static priority scheduling, utilization-based admission control, priority assignment.
Glossary
| Term | Description |
|
|
| f(i)p,k,j(t) | The amount of the traffic with priority p of Class i arriving at Server k at input link j during time interval [0,t) |
| F(i)p,k,j(I) | The traffic constraint function of f(i)p,k,j(t) |
| s(i) | The burst size of a flow of Class i |
| r(i) | The average rate of a flow of Class i |
| D(i) | The end-to-end deadline requirement of traffic of Class i |
| dp,k | The worst case queuing delay suffered by the traffic with priority p at Server k |
| G(i)p,j,k | The set of all flows with priority p of Class i going throught Server k from input link j |
| n(i)p,j,k | The number of flows in Group of Flow G(i)p,j,k |
| a(i)p,k | The ratio of the link server bandwidth allocated to traffic with priority p of Class i at Server k |
| Y(i)p,k | The maximum of the worst case delays experienced by all flows with priority p of Class i before arriving at Server k |
| N(i)p,k | The number of flows of Class i with priority p at Server k |
| M | The number of classes |
| N | The maximum number of available priorities |
| L | The number of input links for a router |
| V | The set of all link servers in network G |
| E | The set of edges in network G |
| C | The link capacity |
1 Introduction
In this paper, we study a methodology for providing absolute
differentiated services for real-time
applications in networks that uses static priority scheduler. We extend the
previous
results on delay analysis, address the priority assignment problem, and
hence are able to
provide a solution that is practical and effective.
1.1 Absolute Differentiated Services
The recent development of the differentiated service (Diffserv) Internet
model is aimed at supporting service
differentiation for aggregated traffic in a scalable manner. Many approaches
have been proposed to realize the Differv model.
At one end of the spectrum, absolute differentiated services [16,17,18]
seek to provide Intserv-type end-to-end absolute
performance measures without per-flow state in network core. In this
approach, the user receives an absolute service
profile (e.g., certain guarantees on bandwidth, or any end-to-end delay).
For example, assuming that no dynamic routing occurs, the premium service
can offer the user a performance level that is similar to that a
leased-line, as long as the user's traffic is limited to a given bandwidth [16].
At the other end of spectrum, relative differentiated services seek
to provide per-hop, per-class relative services [8]. Consequently, the
network cannot provide worst case bounds for a service metric. Instead,
each router only guarantees that the service invariant is locally
maintained, even though the absolute end-to-end service might vary with
networking conditions.
Many real-time applications, e.g., Voice over IP, DoD's C4I, and industrial
control systems,
demand efficient and effective communication services. In this context, by
real time we mean that a packet is delivered from its source to the
destination within a predefined end-to-end deadline. Packets delivered
beyond these end-to-end deadlines are considered useless. Real-time
applications need absolute differentiated services in order to have a
guarantee on the end-to-end delay. Consequently, in this paper, we will
focus on a quality-of-service architecture that provides end-to-end
absolute differentiated services.
Progress has been made to provide absolute differentiated services for
real-time applications in networks with rate-based scheduling algorithms
[18]. In this paper, we consider networks that use static priority
scheduler. Given the static priority schedulers have been supported in many
current routers, our approaches can be easily implemented in the existing
networks.
1.2 Admission Control
Clearly, admission control is critical to provide absolute differentiated
services. In the Diffserv domain, admission control must be realized in a
scalable fashion. We will use Utilization-based Admission Control (UBAC)
approach in this study. The key idea behind the UBAC approach is the
employment of a utilization bound which has the following physical meaning:
as long as the utilization values of links along the path of a flow is not beyond the
bound value, the end-to-end deadline requirement of the flow can be met.
The correctness of the utilization bound is
verified at the system configuration time. Once verified, the use of the
utilization bound
is relatively simple at flow admission time: Upon the arrival of a flow
establishment request,
the admission control admits the flow if the utilization values of links
along the path of the new flow are no more than the bound. Thus, the UBAC
approach eliminates explicit delay computation at admission time, and
helps the system to scale up.
1.3 Flow-Population-Insensitive Delay Analysis
The challenge of using the UBAC method is how to verify the correctness of
a utilization bound
at the configuration time. Obviously, the verification will have to be
involved with
delay analysis. We will follow the approach proposed by Cruz [5] for
analyzing delays.
While Cruz's approach has been widely investigated in many studies,
we need to modify
it in order to achieve our objective. In particular, the delay derivation
proposed in
[5] depends on the information of flow population, i.e., the number of
flows at input
links and the traffic characteristics (e.g., the average rate and burst
size) of flows.
However, in our case the delay analysis is done at the system configuration
time and hence
the information of flow population is not available. We will extend the Cruz's
approach and develop a method that allows us to analyze the delays without
depending on
the dynamic status of flow population.
1.4 Priority Assignment
Priority Assignment is an inherent issue in the networks with
static priority scheduling. As priority assignment has direct impact on the
delay performance of individual packets, it must be carefully addressed. In
Diffserv domain, applications are differentiated by their classes.
Accordingly, many previous studies assume that
priorities are assigned based on classes only, typically, the flows in a
class are assigned by the same priority [4]. Flows from different classes are
given different priority. We study more
generalized priority assignment algorithms. We allow that the flows in a
class may be
assigned by different priorities and flows from different classes may share a
same priority. While the proposed algorithms are still relatively
simple and efficient,
we find they are effective in achieving higher utilization bounds.
1.5 Organization of this Paper
The rest of the paper is organized as follows. In Section II, we describe
previous work that is related to our work. The underlying network and
traffic models for this study are introduced in Section III. In Section IV,
we introduce our proposed architecture on providing absolute differentiated
services in the networks with static priority scheduling.
In Section V, we derive delay computation formula that is insensitive to
the information of flow population. In Section VI, we discuss our heuristic
algorithms for
priority assignments. In Section VII, we illustrate with extensive
experimental data that the utilization achieved by our new algorithms is
much higher than traditional methods. A summary of this paper and
motivation of future work are given in Section VIII.
2 Previous Works
2.1 Absolute Differentiated Services
A good survey to the recent work on absolute differentiated services and relative
differentiated services has been done in [17]. Here, we compare
our work with others from the view point of providing absolute differentiated services. Nicols et. al. [16] have proposed
premium service model that provides the equivalent of a dedicated link between two
access routers. It provides absolute differentiated
services in
priority-driven scheduling networks with two priorities, in which the high
priority is reserved for premium service. The algorithm in [6] provides both guaranteed and statistical rate and delay bounds, and
addresses scalability through traffic aggregation and statistical multiplexing.
Stoica and Zhang describe
an architecture to provide guaranteed service without per-flow state management by
using a technique called dynamic packet state (DPS) [18]. Our work is
based on static priority scheduling algorithm, which is relatively simple and widely
supported.
2.2 Admission Control
Admission control is a mean to provide service guarantees. Admission control has
been investigated widely [7,9,15]. They are different from each other in the senses of the
different scheduling schemes involved, and their complexity.
The traditional admission control in the static priority scheduling network is very
complicated. Due to absence of flow separation, for any new arrival flow request, the
traditional admission control need perform an explicit delay computation and verification
for all existing flows plus the new flow. This procedure introduces
significant flow-number-dependent run-time overhead. In this paper, Utilization-based
Admission Control (UBAC) is adopted, and the complexity is reduced dramatically.
Utilization-based Admission Control (UBAC) was first proposed in
[14] on preemptive scheduling of periodic tasks. A variety
of the utilization levels for different settings have been found,
e.g., 69% and 100% for periodic tasks on a single
server using rate-monotonic and earliest-deadline-first scheduling,
respectively[14], or 33% for synchronous traffic over FDDI networks [22].
In this paper, we adopt this approach in providing absolute differentiated services in static
priority scheduling networks.
2.3 Priority Assignment
This paper focuses on priority assignment in static priority scheduling networks for real-time communication applications, within Diffserv domain. [5] proposed a two-priority assignment scheme for a ring network. [13] described and examined various priority assignment methods for ATM networks. Our work is the very first on priority assignment for proving absolute differentiated services.
3 Network and Traffic Models
In this section, we describe the model and define the terminology that will be used in the rest of this paper.
- Network, Routers, and Links:
The Diffserv architecture distinguishes two types of routers:
Edge routers are located at the boundary of the network, and provide support for traffic policing. Core routers are within the interior of the network. We assume all routers are L ×L, and all output links are of capacity C, in bits per second.
- Server:
For the purpose of delay computation, we follow standard practice and model a router as a set of servers, one for each router component, where packets can experience delays. Packets are typically queued at the output buffers, where they compete for the output link. We, therefore, model a router as a set of output link servers. All other servers (input buffers, non-blocking switch fabric, wires, etc.) can be eliminated by appropriately subtracting constant delays incurred on them from the deadline requirements of the traffic.
- Server Graph:
Consequently, the network can be modeled as a graph G = (V, E) of connected link servers. The link servers in set V are connected through either links in the network or paths within routers, which both make up the set of edges E in the graph.
- Flows:
We call a stream of packets between a sender and receiver a flow. Packets of a flow are transmitted along a single path, which we model as a list of link servers.
- Classes of Traffic:
Following the Diffserv architecture, flows are partitioned into classes. QoS requirement and traffic specifications of flows are defined on a class-by-class basis. We use M to denote the total number of classes in a network. We assume that at each link server, a certain percentage of bandwidth is reserved for individual traffic classes. Let a(i) denote the percentage of bandwidth reserved for Class i at evry server.
- Priorities of Services:
In a router with static priority scheduler, packets are served based on
their priorities. Packets with higher priorities will be served prior to those with lower priorities. We use N to denote the total number of priorities that a static priority scheduler can support in a router. We use a(i)p, k to denote the ratio of bandwidth reserved for traffic with priority p of Class i going through Server k. Thus for any k, 1 £ k £ |V|, a(i) = åp = 1Na(i)p,k. The admission control uses a(i)p,k to determine if a flow with priority p of Class i can be admitted. We assume that the priority assignment algorithm (to be discussed in Section VI) will also partition a(i) into a sequence of values a(i)p,k for each server. In this paper, all flows with priority p in Class i going through Server k from input link j form a Group of Flows G(i)p,j,k.
In order to appropriately characterize traffic both at the ingress
router and within the network, we use a general traffic descriptor in form of traffic functions and their independent counterpart, maximum traffic functions.
DEFINITION 1
The traffic function f(i)p,k,j(t) is defined as the amount of the traffic with priority p of Class i arriving at Server k at input link j during time interval [0,t).
Traffic functions are cumbersome to handle and not of much help in admission control, as they are time dependent. A time-independent traffic characterization is given by the traffic constraint function, which is defined as follows [5]:
DEFINITION 2
Function F(i)p,k,j(I) is called the traffic constraint function of f(i)p,k,j(t) if
|
f(i)p,k,j(t+I) - f(i)p,k,j(t) £ F(i)p,k,j(I). |
| (1) |
for any t > 0 and I > 0.
We assume that the source traffic of a flow in Class i is controlled by a leaky bucket with burst size s(i) and average rate r(i). The total amount of traffic generated by this source during any time interval [t,t+I) is bounded by min{CI, s(i) + r(i) I}.
The QoS requirements of flows (in our case, end-to-end delay requirements) are specified on a class-by-class basis as well. For our purpose, we define the end-to-end deadline requirement of Class i traffic to be D(i) and use a triple ás(i),r(i), D(i) ñ to represent Class i traffic.
As no distinction is made between flows belonging to the same class, all flows in the same class are guaranteed the same delay. We use dp,k to denote the worst-case delay suffered by flows with priority p at Server k. We use vector [d\vec] to denote the upper bounds of the delays suffered by the traffic with all priorities at all servers:
|
| |
|
|
|
(d1,1, d1,2, ¼, d1,|V|, d2,1, d2,2, ¼, d2,|V|, |
| |
|
| ¼, dN,1, dN,2, ¼, dN,|V|) |
| (2) |
| |
|
In the following discussion, we will rely heavily on vector notation. If the symbol a(i) denotes some value specific to Class i traffic, then the notation [a\vec] denotes the M-dimensional vector
(a(1),a(2),...,a(M)). We will use the operator ``°" for the inner product and the operator ``|| ·||" for the zero norm, that is,
|
|
|
®
a
|
° |
®
b
|
= |
M
å
i = 1
|
a(i)b(i) |
| (3) |
| |
|
and
|
|
| || |
®
a
|
|| = |
M
å
i = 1
|
|a(i)| . |
| (4) |
| |
|
4 A QoS Architecture for Absolute Differentiated Services
In this section, we introduce an architecture which is used to provide absolute differentiated services in static priority scheduling networks. This architecture consists of three major modules:
- Flow-population-insensitive delay computation and utilization bound verification:
This module is invoked at configuration time. An ingenious flow-population-insensitive delay method is used to
estimate the delay upper bound for every class at each router. This module
verifies whether the
end-to-end delay bound in each feasible path of the network satisfies the
deadline requirement as long as the bandwidth usage on the path is within
a pre-defined limit,i.e. the utilization bound.
- Efficient admission control:
Utilization-based admission control is adopted. As the delay has been verified at configuration time, this module checks only if the bandwidth is available along the path of the new flow.
- Packet forwarding control:
In a router, packets are transmitted according to their priorities which are marked in their header. Within the same priority, packets are served in FIFO order.
For simplicity, we also consider this architecture within a single domain. For each domain, we designate a domain resource manager (DRM), which
is performed after the Bandwidth Broker in [16].
The DRM has access to the whole domain topology and link capacity information. It performs the delay computation and verification at configuration time as well as
admission control at run time.
In addition to forwarding packets, the edge routers participate in
the flow establishment. They are responsible for communicating with the DRM. For communication between edge routers and the DRM, we use the policy client-server protocol, such as COPS [2].
Upon receiving a flow admission request, the ingress router forwards it requests
to the DRM. The DRM invokes its admission control function, and sends a policy (for
example, the admission decision and traffic shaping policing parameters)
to the edge router.
Once a flow is admitted, the edge routers will appropriately filter
the incoming traffic
according to the policies just set. For each packet
passing through the filter, the priority is marked
in the TOS field in the packet header and the packet is forwarded to the appropriate
output links. Core routers then honor the priority in their packet forwarding scheduling.
The information maintained in the DRM is limited to one counter for
each class per priority per link server, requiring very little
memory storage. Also, in admission control the DRM need only check the bandwidth usage along the path of the flow in its local database, making the run time overhead very low. Based on this consideration, we believe that the DRM will
not be a bottleneck for the performance of network.
In the rest of this paper, we will focus on two critical issues that must be addressed in order to realize this architecture: flow-population-insensitive delay computation analysis and priority assignment.
5 Flow-Population-Insensitive Delay Computation
In this section, we will present our new delay computation formula that is insensitive to flow population. We then discuss the approach with which this delay formula is derived.
5.1 Main Result
Generally speaking, with static priority scheduling, the worst-case delays on link servers depend on the number and traffic characteristics of flows competing for the server. Inside the network, the traffic characteristics of a flow at the input of a server depends on the amount of contention experienced upstream by that flow. Intuitively, all the flows currently established in the network must be known in order to compute delays when no flow separation is provided, which is the case when static priority scheduling is used. Delay formulas for this type of systems have been derived for a variety of scheduling algorithms [12]. While such formulas could be used (at quite some expense) for flow establishment at system run-time, they are not applicable for delay computation during configuration time, as they rely on information about flows population.
As the information is not available at configuration time, the worst case delays may be determined under the assumption of the worst case combination of flows has been established. An impractical way is to exhaustively enumerate all possible combinations of flows in the system and compute the delays on the servers for the every possible combination to gain the worst case delays. Fortunately, we can derive an upper bound on the worst case delay without having to exhaust all the flow combinations as shown in the following theorem:
Theorem 1
The worst case queuing delay dp,k suffered by the traffic with priority p at Server k is bounded by
|
|
| dp,k £ |
|
|
å
q £ p
|
( |
®
a
|
q,k
|
° |
®
Z
|
q,k
|
) - (1 - |
å
q £ p
|
|| |
®
a
|
q,k
|
||) |
|
L-|| |
®
a
|
p,k<���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������/font>
|
|| |
|
|
|
|
| (5) |
| |
|
where
|
| |
|
|
| (6) | |
|
|
max
R Î S(i)q,k
|
|
å
j Î R
|
dq,j, |
| (7) |
| |
|
[(a)\vec]q,k is a vector that specifies the ratio of bandwidth reserved for traffic with priority p of all classes going through Server k, and S(i)q,k is the set of all routes passed by the packets of Class i with priority p before arriving at Server k.
Derivation of (5) will be discussed in Section IV.B. Here we would like to make the following observations on Theorem 1.
- Usually a delay computation formula for a server would depend on the state of the server, i.e., the number of flows that are admitted and pass through the server. We note that our new delay formula (5) is independent from this kind of information and just depend on [(s)\vec], [(r)\vec], [(a)\vec]p,k, and L. However, the values of these parameters are available at the time when the system is (re-)configured. Hence, the delay computation formula is insensitive to the flow population information.
- In the delay computation formula in [4], there was an implicit limitation on the relationship of traffic classes and priorities, that is, one traffic class can only have a single priority, and one priority can only be assigned to a single class traffic. This limitation puts a constraint on differentiating service. The new delay formula remove this limitation, providing more flexibility of differentiating service. Our priority assignment algorithms will take advantage of this flexibility and achieve higher network utilization.
- We note that in (5) dp,k depends on Y(i)q,k. Then, according to (7), the value of Y(i)q,k, in turn, depends on the delays experienced at servers other than Server k. In general, we have a circular dependency, as [d\vec] depends on Y(i)q,k, and Y(i)q,k depends on [d\vec]. Hence, the delay values depend on each other and must be computed simultaneously. Define the right hand side of (5) as Fp,k([d\vec]), and
|
| |
|
|
|
(F1,1( |
®
d
|
), F1,2( |
®
d
|
), ¼, F1,|V|( |
®
d
|
), |
| |
|
|
F2,1( |
®
d
|
), F2,2( |
®
d
|
), ¼, F2,|V|( |
®
d
|
), |
| |
|
| ¼,FN,1( |
®
d
|
), FN,2( |
®
d
|
), ¼, FN,|V|( |
®
d
|
)) |
| (8) |
| |
|
The queuing delay bound vector [d\vec] can then be determined by the following vector equation:
Since the unknown vector [d\vec] appears on both sides of (9), an iterative procedure is needed to compute [d\vec].
5.2 The Approach Used to Derive the Delay Formula
In this subsection, we discuss how to derive the delay formula given in (5). We will start with a formula for delay computation that depends on flow population, which we call the general delay formula. We will focus on how to remove its dependency on information of flow population.
For Server k, suppose that the Group of Flows G(i)p,j,k, at some time moment, has n(i)p,j,k traffic flows coming through. Let F(i)p,j,k(I) be the constraint function for the aggregated traffic of G(i)p,j,k. This constraint function can be formulated as the sum of the constraint functions of individual flows, that is,
|
|
| F(i)p,j,k(I) = |
n(i)p,j,k
å
x = 1
|
H(i)p,j,k,x(I) |
| (10) |
| |
|
where H(i)p,j,k,x(I) is the constraint function for the xth flow in G(i)p,j,k. Further, the aggregate traffic of all G(i)p,j,k's , for i = 1,...,M, is constrained by
|
Fp,j,k(I) = |
min
| {C *I , |
M
å
i = 1
|
F(i)p,j,k} |
| (11) |
The worst case delay dp,k of priority p flows at Server k can then easily be formulated in terms of the aggregated traffic constraint functions and the service rate C of the server as follows [12]:
|
dp,k = |
max
I > 0
|
( |
1
C
|
( |
å
q < p
|
|
L
å
j = 1
|
Fq,j,k(I+dp,k) + |
L
å
j = 1
|
Fp,j,k(I) ) - I). |
| (12) |
Substituting (10) and (11) into (12), we observe that the above delay formula depends on flow population, i.e., (12) depends on n(i)p,j,k, the number of flows at each input link, and on the traffic constraint functions H(i)p,j,k,x(I) of the individual flows. This kind of dependency on the dynamic system status must be removed in order to perform delay computations at configuration time.
In the following sections, we describe how we first eliminate the dependency on the traffic constraint functions. Then we eliminate the dependency on the number of flows on each link. The result is a delay formula that can be applied without knowledge of the flow population.
5.2.1 Removing Dependency on Individual Traffic Constraint Functions
We now show that the aggregated traffic function F(i)p,j,k(I) can be bounded by replacing the individual traffic constraint functions H(i)p,j,k,x(I) by a common upper bound H(i)p,k, where H(i)p,k is defined to be the traffic constraint function of that flow with priority p in Class i experiencing the longest delay upstream from Server k.
The delay on each server can now be formulated without relying on traffic constraint functions within the network of individual flows. The following theorem in fact states that the delay for each flow on each server can be computed by using the constraint traffic functions at the entrance to the network only.
Theorem 2
The aggregated traffic of all Group of Flows G(i)q,j,k's , for i = 1,...,M, is constrained by
|
Fq,j,k(I) = |
ì
ï
ï
í
ï
ï
î
| |
|
| |
| |
|
®
n
|
q,j,k
|
°( |
®
h
|
q,k
|
+ |
®
r
|
I), |
|
|
| |
| (13) |
for q = 1,...,p, where
and the worst case delay dp,k of priority p flows at Server k can be bounded by
|
|
| dp,k £ |
Up,k - Vp,k Wp,k
Xp,k
|
|
| (16) |
| |
|
where
|
| |
|
|
|
|
å
q £ p
|
|
L
å
j = 1
|
( |
®
n
|
q,j,k
|
° |
®
h
|
q,k
|
), |
| (17) | |
|
|
C - |
å
q £ p
|
|
L
å
j = 1
|
( |
®
n
|
q,j,k
|
° |
®
r
|
), |
| (18) | |
|
| C - |
å
q < p
|
|
L
å
j = 1
|
( |
®
n
|
q,j,k
|
° |
®
r
|
), |
| (19) |
| |
|
and
Proof of Theorem 2 is given in Appendix A.
The delay computation using Equation (16) still depends on the number of flows on all input links. In the next section, we describe how to remove this dependency.
5.2.2 Removing Dependency on the Number of Flows on Each Input Link
As we described earlier, admission control at run-time makes sure that the utilization of Server k allocated to flows with priority p of Class i does not exceed a(i)p,k. In other words, the following inequality always holds:
|
|
L
å
j = 1
|
n(i)p,j,k r(i) £ a(i)p,k C. |
| (21) |
The number of flows on each input link is, therefore, subject to the following constraint:
|
N(i)p,k = |
L
å
j = 1
|
n(i)p,j,k £ |
a(i)p,k
r(i)
|
C, |
| (22) |
where a(i)p,k is the ratio of the link bandwidth allocated to Class i traffic with priority p at Server k.
To maximize the right hand side of (16), we should maximize Up,k and minimize Vp,k, Xp,k, and Wp,k. Under the constraint of (22), these parameters can be bounded for all possible distribution n(i)p,j,k of numbers of active flows on all input links, as the following theorem shows:
Theorem 3
If the worst case queuing delay is experienced by the traffic with priority p at Server k, then,
|
| |
|
|
|
|
å
q £ p
|
( |
®
a
|
q,k
|
° |
®
Z
|
q,k
|
) C, |
| (23) | |
|
|
(1 - |
å
q £ p
|
|| |
®
a
|
q,k
|
||) C, , |
| (24) | |
|
| (1 - |
å
q < p
|
|| |
®
a
|
q,k
|
||) C, |
| (25) |
| |
|
and
where Up,k, Vp,k, Xp,k, and Wp,k are defined in (17), (18), (19), and (20).
Proof of Theorem 3 is given in Appendix B. Now, if we substitute all the bounds in (23), (24), (25), and (26) into (16), then (5) follows.
6 Priority Assignment
In this section, we address priority assignment algorithms. Our priority
assignment algorithms utilizes the flow-population-insensitive delay
formula derived in the previous section. This makes it possible to determine
the priorities for the flows at the configuration time, reducing the
run-time overhead of flow admission control.
6.1 Outline of Algorithm
Note that upon arrival of a request for a flow establishment, the
network management assigns a priority to the flow (that is, all the packets
of this flow will be transmitted with this priority, if the flow is
admitted) and performs the admission control. The priority assignment
algorithms can be classified into two categories: dynamic and
static. With a dynamic priority assignment algorithm, the system
examines the dynamic status of the network (e.g., the active flows and
their characteristics) and decides a priority that may best meet its needs.
Needless to say, the dynamic algorithms will have better network
performance (in terms of admission probability and network utilization),
but may suffer for the runtime overhead.
In this paper, we adopt the static approach. With a static priority
assignment, the mapping from a flow to a priority is pre-determined. Once ���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������a
mapping from flow to priority is determined, the assignment of a priority
to a flow, becomes simply a table look up, which has much
less overhead than many dynamic methods.
Depending on how a class of flows are mapped to priorities, we investigate
three kinds of methods for priority assignments:
- Algorithm one-to-one: With this algorithm, all the flows in a class
are mapped into the same priority. Flows in different classes are mapped
into different priorities. Given that we want to meet the deadline
requirements of the flows, we let the class with the least deadline take
the highest priority. The advantage of this method is its simplicity. But,
it assigns priorities based on the information of classes only and does not
take into account the fact that even within the same class, a flow may needs a
higher priority than another because, say, the former takes a longer route. In [4], this algorithm is adopted.
-
Algorithm one-to-many: With this algorithm, flows from a class may be
assigned to different priorities. But, flows in different class may not
share a priority. In Section VI.B we present a version of this algorithm.
Generally speaking, this algorithm can recognize the different requirements
of flows in a class and assign them different priorities, hence improving
the network performance. The algorithm is still relatively simple, but it
may use too many priorities given it does not allow priorities to be shared
by flows from different classes.
-
Algorithm many-to-many: This is the most general form of priority
assignment algorithms we study here. It is the same as the one-to-many
algorithm but sharing priorities is allowed by flows even if they are from
different classes. Given its generality, this algorithm can achieve better
performance than other two.
6.2 Details of Algorithms
We will first focus on Algorithm one-to-many. We will then show that
Algorithms one-to-one and
many-to-many are
a special case and generalization of Algorithm one-to-many, respectively.
As mentioned above, in this paper, we adopt static priority assignment
approach. With this approach, the mapping from flow to priority is
pre-determined, and stored in a table (to be used by the admission control module at admission time and
by edge routers upon a packet arrival. The purpose of our static priority
assignment algorithm is to generate a priority assignment table. A priority
assignment table consists of a list of entries. An
entry contains fields of class, source, destination, and priority, etc. Note that the first three fields of an entry áclass, source, destination ñ represent a group of
potential flows which belongs to the same traffic class, and uses the
same path from the source and to the destination.
Table 1:
A Example of Priority Assignment Table
| Class | Source | Destination | Priority |
|
|
| 1 | Node 2 | Node 3 | 2 |
| 1 | Node 4 | Node 7 | 3 |
| ... | ... | ... | ... |
| 2 | Node 6 | Node 1 | 1 |
INPUT: network server graph G = (V, E), flow traffic and
deadline parameters for all the classes, a network
utilization a(i), i = 1,...,M.
1. Initialize the priority assignment table, and fill the proper
value into the fields of entries except that the priority
field is initialized ``undefined''.
2. for i from M to 1 do
assign all entries ái, source, destination, priority ñ
of Class i into subset Si and push subset Si into Stack SS;
3. p = 0;
4. While Stack SS is not empty
4.1. p = p+1;
4.2. if p > N /* no more priority available */
return ``false'';
4.3. Pop a subset S from Stack SS;
4.4. Assign p to the priority field of all the entries in S;
4.5. Use delay formula computed by using in (9)
to update the end-to-end delay of potential flows
represented by entries in S;
4.6. If no flow represented by an entry in S misses its
deadline
Continue;
4.7. else
4.7.1. if S consists of a single entry
return ``false'';
4.7.2. else
4.7.2.1. call Procedure Bi-Partition(S),
and obtain two subsets: Sx, Sy
4.7.2.2. push Sy and Sx into Stack SS;
5. return the current priority assignment table and values of a(i)p,k;
Figure 1: Algorithm One-to-Many
Figure 1 show our one-to-many priority assignment algorithm.
The algorithm uses a stack to store subsets of entries of which the priority fields
are to be
assigned. Entries in each subset can potentially assigned to the same
priority. The subsets are
ordered in the stack in accordance to their real-time requirements. The
subset with entries that
represent flows with the most tight deadline and/or laxity is at the top of
the stack.
After its initialization, the algorithm works iteratively. In an iteration,
the program stops
and declares "failure"
if it is found that no more priority is available (Step 4.2). Otherwise,
a subset is popped
out from the stack. The algorithm then assigns the best (highest) available
priority to the
entries in the subset if the deadlines of the flows represented by those
entries can be met.
However, if some of the deadline tests cannot be passed, a procedure
Bi-Partition is called
to partition the subset into two subsets: one contains those entries with
relatively shorter laxity and
another with relatively larger laxity. The idea here is that if we assign a
higher priority
to the former and a lower priority to the latter, we may pass the deadline
tests for both.
This is realized by pushing two new subsets into the stack in the proper
order and letting the
future iteration deal with the priority assignment. Procedure Bi-Partition
also properly splits values in a(i)p, k to reflect the partitioned
subsets.
There is a case in which
partitioning a subset cannot be done: a subset may contain only one entry
and hence it is too small to be
partitioned (Step 4.7.1). In this case, the program declares "failure". The program
iterates until either it declares "failure" or it exhausts all the subsets in
the stack. In this case, a successful
priority assignment has been found and the program returns the assignment
table.
Because the size of a subset is
halved at every iteration step, the worst case time complexity of the
algorithm is in the
order of O(M log|V|) in the number of delay computations. In spite
of its low time complexity,
as we will see, this algorithm does perform reasonably well.
Algorithm one-to-one is a special case of algorithm one-to-many presented
in Figure 1. For
algorithm one-to-one, no subset partition is allowed (otherwise entries in
one class will be assigned to different priorities - a violation of the
one-to-one principle).
Thus, if we modify the code in Figure 1 so that it returns "fail" whenever
a failure on deadline test is found (Step 4.7), it becomes the
code for Algorithm one-to-one.
On the other hand, we can generalize algorithm one-to-many to become algorithm
many-to-many.
Recall that algorithm many-to-many allows the priorities to be shared by
flows in different
classes. Note that sharing a priority is not necessary
unless the priorities have been used up. Following this idea, we can
modify the code
in Figure 1 so that it becomes the code for algorithm many-to-many. At Step 4.2, when it is
discovered that all the available priorities have been used up, do not
return "fail", but
assign the entries with the priority that has just be used. In the case the
deadline test fails,
assign these entries with a higher priority (until the highest priority has
been assigned).
Due to the space limitations, we will not present the complete code of
algorithms one-to-one and
many-to-many here. Nevertheless, we will study the performance of all the
three algorithms in
the next section.
7 Experimental Evaluation
In this section, we evaluate the performance of the systems that use our new delay analysis techniques and priority assignment algorithms discussed in the previous sections. We will first define a performance metric, then describe the system configuration and present the performance results.
7.1 Experimental Model
- Performance Metric:
Recall that we use Utilization-based Admission Control (UBAC) in our study. This approach define a utilization level, as long as the link utilization along the path of a flow is not beyond the bound value, the end-to-end deadline of the flow is guaranteed. Define the worst-case achievable utilization (WCAU) to be the maximum of total utilization bound for all classes. We
use this metric to measure the performance of the systems. For a given network with a priority assignment algorithm, its WCAU value is obtained by performing a binary sreach in conjunction with the priority assignment algorithm discussed in Section VI.
- Network:
We evaluate our priority assignment algorithms in two suites of networks: one suite is the classical MCI network; another suite is randomly generated networks. In this experiment, we adopt GT-ITM to generate network topologies [20]. Particularly, we generate 50 samples for each kind of networks with different number of nodes ranging from 10 to 20 2. We assume that all links in the simulated networks have the same capacity of 100 Mbps. All link servers in the simulated networks support the scheduling algorithm with 8 priorities.
- Traffic Model:
We assume that there are three classes of traffic: á 640 bits, 32,000 bps, 50 ms ñ, á 1,280 bits, 64,000 bps, 100 ms ñ, and á 1,920 bits, 96,000 bps, 150 ms ñ. Any pairs of nodes in the simulated networks may request a flow in any class. All the traffic will be routed along the shortest paths in term of number of hops from source to destination.
7.2 Numerical Results and Observations
- MCI network:
The numerical results on MCI network are shown as follows
Table 2: The WCAU Values of the MCI Network
| Algorithm | One-to-One | One-to-Many | Many-to-Many |
| WCAU | 0.48 | 0.63 | 0.73 |
From Table II, we can observe that Algorithm Many-to-Many can achieve the highest WCAU among the three priority assignment algorithms, and Algorithm One-to-Many can achieve better WCAU than Algorithm One-to-One, in the MCI networks. This is expected because Algorithm Many-to-Many makes full use of the flexibility of delay computation in priority assignment.
- Randomly generated networks:
Figure 2 shows the maximum utilization results for the networks with the different numbers of nodes. Particularly, Figure 2 (a) is corresponding to the case when the diameter of networks is less than or equal to 6, and Figure 2 (b) is corresponding to the case when the diameter of networks is larger than 6.
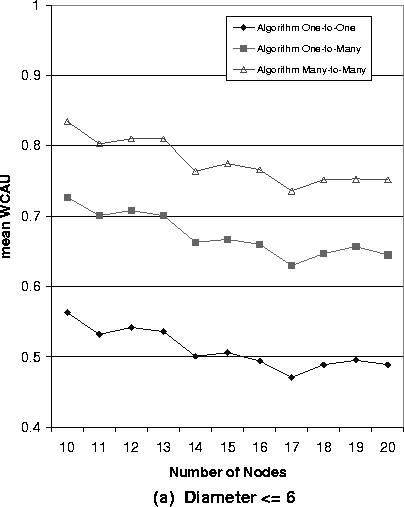
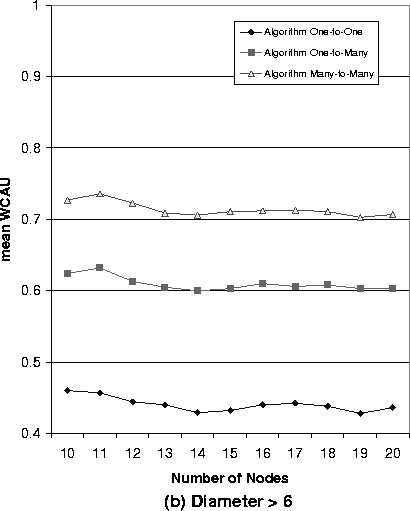
Figure 2:
The WCAU Values of Randomly Generated Networks
From Figure 2, we can make the following observations:
- We found that Algorithm Many-to-Many can always achieve the highest WCAU
among the three algorithms, and Algorithm One-to-Many can achieve better max
utilization than Algorithm One-to-One, in the networks with the same number of
nodes. For example, when the number of nodes is 15, for the case of Diameter
£ 6, the mean WCAU of Algorithm Many-to-Many is 10.6%
higher than that of Algorithm One-to-Many, and is 26.7% higher than that of
Algorithm One-to-One. These observations can be explained by the fact that
Algorithm Many-to-Many has the highest flexibility in assigning priorities among
the three algorithms.
- the diameter of network has an evident impact on the maximum utilization
performance to all the priority assignment algorithms. The network with a large
diameter in the same algorithm always has less maximum utilization than the one
with small diameter. For example, when the the number of nodes is 15, the WCAU
of Algorithm One-to-Many in the case of Diameter £
6, is 7.4% higher than that in the case of Diameter £ 6. The reason is that flows in big networks (in the sense of diameter)
usually suffer larger end-to-end delay than flows do in small networks.
8 Conclusions
In this paper, we have proposed a methodology for providing absolute
Differentiated Services for real-time applications in networks that uses static
priority scheduler. Given the static priority schedulers are widely supported by
the current routers, we believe that our approach has resulted in is a practical
and effective solution to support real-time applications in the existing
network.
We have used Utilization-based Admission Control (UBAC) approach which uses
a configuration-time verification to determine a safe utilization level of
servers. Admission control at runtime then is reduced to simple utilization
tests on the servers along the path of the new flow. Hence, the approach is
scalable.
Obviously, the verification will have to be involved with delay analysis.
Cruz's delay derivation depends on flow population information, which is not
available at the system configuration time. We have extended Cruz's approach and
developed a method that allows us to analyze the delays without depending on the
dynamic status of flow population. Furthermore, we have designed several
priority assignment algorithms, which are shown to be effective in achieving
higher utilization bounds.
Extensive performance evaluation is made to the systems that used our new
delay analysis techniques and priority assignment algorithms. We found that
Algorithm Many-to-Many could achieve very high network utilization both in a
well-known network and randomly generated networks.
Our methodology presented in this paper can be easily extended to deal with
statistical delay guarantees. Much progress has been made in derivation of
statistical delay bounds [10,3,11,19]. However,
all these previous results require information on flow population to obtain the
statistical delay bounds. For example, in [10] statistical delay bounds are obtained by using
approximated normal distribution, of which the parameters, in turn, depend on
the flow population. Our method on eliminating flow-population dependency in
delay computation can be applied in this situation to make delay derivation
insensitive to flow population. This should help to provide absolute
differentiated services to applications that require statistical delay
guarantee.
Appendix A: Proof of Theorem 2
Theorem 2:
The aggregated traffic of all Group of Flows G(i)q,j,k's , for i = 1,...,M, is constrained by
|
Fq,j,k(I) = |
ì
ï
ï
í
ï
ï
î
| |
|
| |
| |
|
®
n
|
q,j,k
|
°( |
®
h
|
q,k
|
+ |
®
r
|
I), |
|
|
| |
| (27) |
for q = 1,...,p, where
and the worst case delay dp,k of priority p flows at Server k can be bounded by
|
|
| dp,k £ |
Up,k - Vp,k Wp,k
Xp,k
|
|
| (29) |
| |
|
where
|
| |
|
|
|
|
å
q £ p
|
|
L
å
j = 1
|
( |
®
n
|
q,j,k
|
° |
®
h
|
q,k
|
), |
| (30) | |
|
|
C - |
å
q £ p
|
|
L
å
j = 1
|
( |
®
n
|
q,j,k
|
° |
®
r
|
), |
| (31) | |
|
| C - |
å
q < p
|
|
L
å
j = 1
|
( |
®
n
|
q,j,k
|
° |
®
r
|
), |
| (32) |
| |
|
and
In order to prove Theorem 2, we need following lemmas:
LEMMA 1
The aggregated traffic of Group of Flows G(i)p,j,k is constrained by
|
F(i)p,j,k(I) = |
ì
ï
í
ï
î
| |
|
| |
| |
n(i)p,j,k (h(i)p,k + r(i) I), |
|
|
| |
| (34) |
where
|
t(i)p,j,k = |
n(i)p,j,k h(i)p,k
C - n(i)p,j,k r(i)
|
|
| (35) |
Recall that we assume that all flows of Class i have the same constraint function H(i)(I) at the entrance to the network, that is,
|
H(i)(I) = |
min
| {C I, s(i)+ r(i) I}. |
| (36) |
Let Y(i)p,j,k,x be the total worst case queuing delay experienced by the xth flow before arriving at Server k. Recall that Y(i)p,k is the maximum of the worst case queueing delays:
According to Theorem 2.1 in [5],
|
H(i)p,j,k,x(I) £ H(i)(I+Y(i)p,j,k,x) £ H(i)(I+Y(i)p,k). |
| (38) |
We can, therefore, bound F(i)p,j,k as follows:
|
|
| F(i)p,j,k(I) £ |
n(i)p,j,k
å
x = 1
|
H(i)p,j,k,x(I) £ |
n(i)p,j,k
å
x = 1
|
H(i)(I+Y(i)p,k). |
| (39) |
| |
|
Substituting (36) into (39), we have
|
F(i)p,j,k(I) £ |
min
| {n(i)p,j,k C, n(i)p,j,k (h(i)p,k + r(i) �����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������I)}. |
| (40) |
On the other hand, the total amount of traffic that can be transmitted over Input Link j of Server k during any time interval I is constrained by the link capacity C. Therefore, we have
Synthesizing (40) and (41), we verify the values of F(i)p,j,k(I) and t(i)p,j,k(I) to be as claimed.
Similarly, bounds can be defined for the aggregated traffic on an input link of all classes with given priority, as the following lemma shows.
LEMMA 2
The aggregated traffic of all Groups of Flows G(i)p,j,k's , for i = 1,...,M, is constrained by
|
Fp,j,k(I) = |
ì
ï
ï
í
ï
ï
î
| |
|
| |
| |
|
®
n
|
p,j,k
|
°( |
®
h
|
p,k
|
+ |
®
r
|
I), |
|
|
| |
| (42) |
where
Similar to the proof of Lemma 1, we have
|
Fp,j,k(I) = |
min
| {C I , |
M
å
i = 1
|
F(i)p,j,k} |
| (44) |
Note that each F(i)p,j,k(I) is a two-piecewise linear continuous function of I, and åi = 1MF(i)p,j,k(I) is still a piecewise linear continuous function of I. The value t(i)p,j,k identifies the intersection of the two linear segments, and is called the flex point of F(i)p,j,k(I). All t(i)p,j,k's are also flex points of åi = 1MF(i)p,j,k(I).
We can find that tp,j,k ³ t(i)p,j,k for all classes i, and if I £ tp,j,k, then åi = 1MF(i)p,j,k(I) ³ C I; if I > tp,j,k, then åi = 1MF(i)p,j,k(I) = [n\vec]p,j,k°([(h)\vec]p,j,k+ [(r)\vec] I). Therefore,
|
Fp,j,k(I) = |
ì
ï
ï
í
ï
ï
î
| |
|
| |
| |
|
®
n
|
p,j,k
|
°( |
®
h
|
p,k
|
+ |
®
r
|
I), |
|
|
| |
| (45) |
Now we are ready to prove Theorem 2.
Let
Then, Fq,j,k can be rewritten as
for q = 1,...,p, with
|
tq,j,k = |
Aq,j,k
C-Bq,j,k
|
. |
| (49) |
Following [12], we have the following formula that indicates how long an newly arrival packet with priority p of Class i can be delayed at Server k, assuming that a static priority scheduling discipline at the server:
|
dp,k = |
1
C
|
|
max
I > 0
|
( |
å
q < p
|
|
L
å
j = 1
|
Fq,j,k(I+dp,k) + |
L
å
j = 1
|
Fp,j,k(I) ) - I. |
| (50) |
Let tq < p,j,k and tp,j,k be the flex points of traffic constraint function for traffic coming from the Input Link j of Server k with priority higher than p and with priority p, respectively. Further, let Tq < p,j,k be the maximum busy interval of the traffic constraint function for traffic coming from Input Link j of Server j with priority higher than p, and tmax is the maximum flex point for the total aggregate traffic in (50). Define
|
t1 = |
L
max
j = 1
|
{tq < p,j,k}, t2 = |
L
max
j = 1
|
{tp,j,k} |
| (51) |
We know that tmax = max(t1-dp,k, t2). Here t1-dp,k £ 0 since dp,k ³ Tq < p,j,k ³ t1. So tmax = t2. Let s be the slope of the aggregate traffic function. We find that s £ C if I £ tmax; s ³ C if I ³ tmax. Therefore, the worst-case queuing delay dp,k suffered by the traffic with priority p at Server k will happen at
|
I = tmax = |
L
max
j = 1
|
{tp,j,k} |
| (52) |
We can, therefore, eliminate the max operator from (50). By appropriately substitute (52) into (50), we have
|
| |
|
|
|
|
1
C
|
( |
å
q < p
|
|
L
å
j = 1
|
Fq,j,k( |
L
max
j = 1
|
{tp,j,k}+dp,k) |
| |
|
|
+ |
L
å
j = 1
|
Fp,j,k( |
L
max
j = 1
|
{tp,j,k}) ) - |
L
max
j = 1
|
{tp,j,k} |
| (53) | |
|
|
|
1
C
|
( |
å
q £ p
|
|
L
å
j = 1
|
Aq,j,k+ |
å
q £ p
|
|
L
å
j = 1
|
Bq,j,k |
L
max
j = 1
|
{tp,j,k})) |
| |
|
| + (C - |
å
q < p
|
|
L
å
j = 1
|
Bq,j,k) dp,k |
| (54) |
| |
|
Solving dp,k from (54), substituting (46) and (47), with some algebraic manipulation we have
|
dp,k = |
Up,k - Vp,k Wp,k
Xp,k
|
|
| (55) |
where Up,k, Vp,k, Wp,k, and Xp,k are defined in (30), (31), (32) and (33), respectively.
Appendix B: Proof of Theorem 3
Theorem 3:
If the worst case queuing delay is experienced by the traffic with priority p at Server k, then,
|
| |
|
|
|
|
å
q £ p
|
( |
®
a
|
q,k
|
° |
®
Z
|
q,k
|
) C, |
| (56) | |
|
|
(1 - |
å
q £ p
|
|| |
®
a
|
q,k
|
||) C, , |
| (57) | |
|
| (1 - |
å
q < p
|
|| |
®
a
|
q,k
|
||) C, |
| (58) |
| |
|
and
where Up,k, Vp,k, Xp,k, and Wp,k are defined in (30), (31), (32) and (33).
In order to prove Theorem 3, we need the following lemma:
LEMMA 3
The worst case queuing delay at Server k by traffic with priority p of Class i is experienced when the number of flows N(i)q,k on each input link is maximized; that is, for all i = 1, ¼, M, N(i)q,k reaches its upper bound
3
where
|
b(i)p,k = |
a(i)p,k
r(i)p,k
|
|
| (61) |
Since
|
dp,k = |
1
C
|
|
max
I > 0
|
( |
å
q < p
|
|
L
å
j = 1
|
Fq,j,k(I+dp,k) + |
L
å
j = 1
|
Fp,j,k(I) ) - I |
| (62) |
we know that the larger Fq,j,k(I), the larger dp,k. Furthermore, since Fq,j,k(I) is the aggregated traffic of Class i with priority p at Server k, we know that the larger N(i)q,k, the larger Fq,j,k(I). Therefore, when the number of flows on each link is maximized, then the traffic of Class i with priority p will experience the worst case queuing delay at the server.
Now we are ready to prove Theorem 3.
Since N(i)p,k = b(i)p,k C, substituting it into Equation (56), we then have
|
| |
|
|
|
|
å
q £ p
|
( |
®
N
|
q,k
|
° |
®
h
|
q,k
|
) = |
å
q £ p
|
( |
®
b
|
q,k
|
C° |
®
h
|
q,k
|
) |
| (63) | |
|
| C - |
å
q £ p
|
( |
®
N
|
q,k
|
° |
®
r
|
) = C - |
å
q £ p
|
( |
®
b
|
q,k
|
C° |
®
r
|
) |
| (64) |
| |
|
and
|
| |
|
|
| C - |
å
q < p
|
( |
®
N
|
q,k
|
° |
®
r
|
) = C - |
å
q < p
|
( |
®
b
|
q,k
|
C° |
®
r
|
) |
| (65) |
| |
|
since [(b)\vec]p,k��������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������°[(r)\vec] = ||[(a)\vec]p,k|| and [(b)\vec]p,k°[(h)\vec]p,k = [(a)\vec]p,k°[Z\vec]p,k, Up,k, Vp,k, Xp,k can be verified as claimed.
For Wp,k, we have the following argument. If we will treat all variables n(i)p,j,k to be real numbers, then we have the following optimization problem.
|
| |
|
|
|
Wp,k = |
N
max
j = 1
|
{tp,j,k} |
| (66) | |
|
| (67) | |
|
|
|
®
n
|
p,j,k
|
³ |
®
0
|
, j = 1,...,L |
| (68) | |
|
|
L
å
j = 1
|
|
®
n
|
p,j,k
|
= |
®
b
|
p,k
|
C, i = 1,...,M |
| (69) |
| |
|
Without loss of generality, we assume that the input links are ordered according to the size of the flex points:
|
Wp,k = tp,1,k ³ tp,2,k ³ ... ³ tp,L,k |
| (70) |
- Firstly, We can show that when the problem reaches its optimal value Wp,k = tp,1,k, all inequalities in (70) will become equalities. Otherwise, there exists some inequality tp,j0,k > tp,j0+1,k. It's easy to show that with respect to any n(i)p,j,k, tp,j,k is an increasing continuous function. There must exists a nonzero n(i0)p,j0,k. Then by choosing sufficiently small e, decreasing n(i0)p,j0,k by e, increasing n(i0)p,j0+1,k by e, and keeping them nonnegative, we have tp,j0,k ³ tp,j0+1,k. We see that (70) is still true, but tp,j0,k is decreased, and tp,j0-1,k > tp,j0,k. Following this way, eventually we can decrease Wp,k = tp,1,k. This contradicts to (66). Thus, we have
|
Wp,k = tp,1,k = tp,2,k = ... = tp,L,k |
| (71) |
- Applying the formula w = [(a1)/( b1)] = [(a2)/( b2)] = ... = [(aL)/( bL)] = [(a1+a2+...+aL)/( b1+b2+...+bL)] in (71), we have
|
Wp,k = |
|
|
L
å
j = 1
|
|
®
n
|
p,j,k
|
° |
®
h
|
p,k
|
|
|
C- |
L
å
j = 1
|
|
®
n
|
p,j,k
|
° |
®
r
|
|
|
= |
|
|
| (72) |
From (71), we find that for any assignment of n(i)p,j,k satisfying (68) and (69), there exists only one optimal Wp,k, even though there exist multiple assignments of n(i)p,j,k. We find that
|
|
®
n
|
p,j,k
|
= |
®
b
|
p,k
|
|
C
L
|
, j = 1,...,L |
| (73) |
is one of assignments to the optimal solution.
For the original problem, the values of all n(i)p,j,k are integers, then the optimal Wp,k in this case should be the least integer larger than the one in the real solution, since generally the optimal solution with more constrains will become worse. Thus
References
- [1]
-
S. Blake, D. Black, M. Carlson, E. Davies, Z. Wang, and W. Weiss,
An Architecture for Differentiated Service,
RFC 2474, Dec. 1998.
- [2]
-
J. Boyle, R. Cohen, D. Durham, S. Herzog, R. Rajan, and A. Sastry,
The COPS (Common Open Policy Service) Protocol,
Internet-Draft, Feb. 1999.
- [3]
-
C. Chang,
Stability, queue length, and delay of deterministic and stochastic queueing networks,
IEEE Transactions on Automatic Control, 39(5):913-931, May 1994.
- [4]
-
B. Choi, D. Xuan, C. Li, R. Bettati and W. Zhao,
Scalable QoS Guaranteed Communication Services for Real-Time,
Proc. of ICDCS, 2000.
- [5]
-
Rene L. Cruz,
A Calculus for Network Delay, Part I and Part II,
IEEE Transactions on Information Theory, Vol. 37. Jan. 1991.
- [6]
-
R. L. Cruz.
SCED+: efficient management of quality of service guarantees,
Proceedings of INFOCOM'98, 1998.
- [7]
-
A. Dailianas and A. Bovopoulis,
Real-time admission control algorithms with delay and loss guarantees
in ATM networks,
Proceedings of INFOCOM'94, pages 1065-1072, 1994.
- [8]
-
C. Dovrolis, D. Stiliadis and P. Ramanathan,
Proportional Differnetiated Serives: Delay Differentation
and Packet Scheduling
ACM SIGCOMM 1999.
- [9]
-
V. Firoiu, J. Kurose, and D. Towsley,
Efficient admission control for EDF schedulers,
Proceedings of Inforcom'97, 1997.
- [10]
-
E. Knightly,
Enforceable quality of service guarantees for bursty traffic streams,
Proceedings of Inforcom'98, 1998.
- [11]
-
J. Kurose,
On computing per-session performance boundes in high-speed multi-hop computer networks,
ACM Sigmetrics'92, pages 128-139, 1992.
- [12]
-
C. Li, R. Bettati, and W. Zhao,
Static priority scheduling for ATM networks,
Proceedings of the 18th IEEE Real-Time Systems Symposium, 1997.
- [13]
-
C. Li, R. Bettati, and W. Zhao
Static priority scheduling for ATM networks,
Proc. of the 18th IEEE Real-Time Systems Symposium, 1997.
- [14]
-
C. L. Liu and J. W. Layland,
Scheduling algorithms for multiprogramming in a
hard real time environment,
J. ACM, Vol. 20, No. 1, 1973, pp.46-61.
- [15]
-
J. Liebeherr, D.E. Wrege, and D. Ferrari,
Exact admission control in networks with bounded delay services,
IEEE/ACM Transactions on Networking, 1996.
- [16]
-
K. Nicols, V. Jacobson, L. Zhang,
A Two-bit Differentiated Services Architecture for the Internet,
Internet-Draft, Nov. 1997.
- [17]
-
R. Sivakumar, T. Kim, N. Venkitaraman and V. Bharghavan,
Achieving Per-Flow Weighted Rate Fairness in a Core Stateless Network,
IEEE Conference on Distributed Computing Systems 2000, Taipei, Taiwan, March 2000.
- [18]
-
I. Stoica, H. Zhang,
Providing Guaranteed Services Without Per Flow Management,
ACM SIGCOMM 1999.
- [19]
-
O. Yaron and M. Sidi,
Performance and stability of communication networks via robust exponential bounds,
IEEE/ACM Transactions on Networking, 1(3):372-385, June 1993.
- [20]
-
Eleen W. Zegura, etc.,
http://www.cc.gatech.edu/projects/gtitm/
- [21]
-
Z.-L. Zhang, D. Towsley, and J. Kurose,
Statistical analysis of the generalized processor sharing scheduling discipline,
IEEE Journal of Selected Areas in Communications, 13(6):1071-1080, Aug. 1995.
- [22]
- G. Agrawal, B. Chen, W. Zhao, and S. Davari,
Guaranteeing Synchronous Message Deadlines with the Timed Token Protocol,
IEEE International Conference on Distributed Computing Systems, 1992, pp.468-475.
Footnotes:
1 The authors are with the Department of Computer Science, Texas A&M University, College Station, TX 77843. E-mail: {swang, dxuan, bettati, zhao}@cs.tamu.edu .
2 99 We adopt Waxman 2 method for generating edges.
3 In general, b(i)p,k C is not necessarily an integer. However, in a modern practical system it is very large. For example, if we consider a Gigabit router, C = 109 bps. For voice traffic r(i) = 3.2×104 bps, if a(i)q,k = 15%, b(i)p,k C = [(a(i)q,k)/( r(i))] C = 4687.5. Therefore, in order to simplify notation, we assume that ëb(i)p,k C û » b(i)p,k C.
File translated from TEX by TTH, version 2.25.
On 05 Aug 2002, 12:05.

