Analytical
and Empirical Analysis of Countermeasures to
Traffic Analysis Attacks
Xinwen Fu ,
Bryan Graham, Riccardo Bettati and Wei
Zhao
Department of of Computer Science, Texas
A&M University
E-mail: {xinwenfu, bwg7173, bettati,
zhao}@cs.tamu.edu
Dong Xuan
Department of Computer and Information Science, Ohio
State University
E-mail: xuan@cis.ohio-state.edu
Abstract
This paper studies countermeasures to traffic analysis attacks. A common strategy for such countermeasures is link padding. We consider systems where payload traffic is padded so that packets have either constant inter-arrival times or variable inter-arrival times. The adversary applies statistical recognition techniques to detect the payload traffic rates by using statistical measures like sample mean, sample variance, or sample entropy. We evaluate quantitatively the ability of the adversary to make a correct detection and derive closed-form formulas for the detection rate based on analytical models. Extensive experiments were carried out to validate the system performance predicted by the analytical method. Based on the systematic evaluations, we develop design guidelines for the proper configuration of a system in order to minimize the detection rate.
1 Introduction
A significant portion of the Internet traffic today is encrypted, and there are strong indications that this portion will increase at a high rate. However, encryption alone may not be sufficient for secured communications. A number of non-cryptographic attacks ([5,10,15,,19]) have illustrated how the observations of traffic behavior allow an adversary to infer significant information about participants and their communications. For example, [18] shows that timing analysis of SSH traffic can greatly simplify the breaking of passwords. This paper deals with timing based traffic analysis attacks and their countermeasures.
Link padding is one effective approach in countering traffic
analysis attacks. The idea is based on
Differing from the previous studies, we establish a formal theoretical framework for link padding systems and derive closed-form formulae for estimation of detection rates. Our formulae correctly describe the relationship between detection rate and system parameters such as the padded traffic type, sample size, and location in the network where the adversary can collect traffic samples. We report results from extensive experiments in various situations including local area network in a laboratory, campus networks, and wide area networks. Our data consistently demonstrates the usefulness of our formal model and correctness of performance predicted by the closed-form formulae. Based on the observations, we develop design guidelines that allow a manager to properly configure a system in order to minimize the detection rate.
The rest of this paper is organized as follows. Section 2 briefly reviews the related work and
summarizes that
2 Related
Work
The study of traffic analysis and its countermeasures for computer networks is not new. Baran [2] proposed the use of heavy unclassified traffic to interfere with the adversary's tampering on the links of a security network system for classified communication, and suggested adding dummy, i.e. fraudulent, traffic between fictitious users of the system to conceal traffic loads.
To protect the anonymity of email transmission, Chaum
[3]
proposed the use of a
A survey of countermeasures for traffic analysis is given in [25]. To mask the
frequency, length, and origin-destination patterns of end-to-end communication,
the use of dummy messages is suggested to make the traffic adhere to a
predefined pattern. From the discussion of
The authors in ([12,13,24]) give a mathematical framework to optimize the bandwidth usage while preventing traffic analysis of the end-to-end traffic rates. Timmerman [23] proposes an adaptive traffic masking (hiding) model to reduce the overhead caused by link padding. But, when the rate of real traffic is low, the link padding rate is reduced as well, in order to conserve link bandwidth. Perfect secrecy is violated in this case, as large-scale variations in traffic rates become observable.
Raymond in [15] gives an informal survey of many ad hoc traffic analysis attacks on systems providing anonymous service. One conclusion is that dummy messages must be used to achieve high information assurance for the system. It is even claimed [1] that we have to use padding to each link of an anonymity network (although more research is needed to clear this claim).
In our previous work, NetCamo [9], we describe how to provide end-to-end prevention of traffic analysis while at the same time guaranteeing QoS (worst-case delay of message flows). It turns out that the delay experienced by packets of a protected flow is tightly coupled to the bandwidth required to send both payload and dummy packets. We propose methods such as QoS routing to tackle the QoS problem for systems using link padding strategies.
3 The
System M odel
In this section, we present the model of the network in our study and then discuss link padding mechanisms that are used as a countermeasure for traffic analysis attacks. Finally we formally define the model of the adversary, who uses statistical pattern recognition strategies for traffic analysis attacks.
3.1 Network M odel
In this work, we assume that the network consists of protected subnets, which are interconnected by unprotected networks. Traffic within protected subnets is assumed to be shielded from observers. Unprotected network can be public networks (e.g., the Internet), or networks that are deployed over an easily accessible broadcast medium. These networks are accessible to observation by third-parties, and are therefore open to traffic analysis. This model captures a variety of situations, ranging from battleship convoys (where the large-scale shipboard networks are protected and the inter-ship communication is wireless) to communicating PDAs (where the protected networks consist of single nodes).
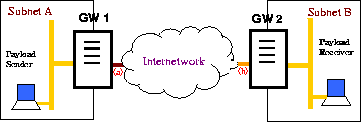
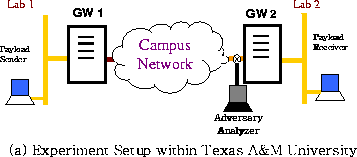
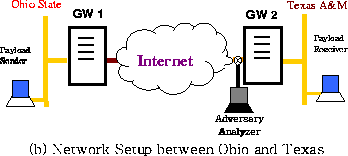
Figure 1 illustrates the setup of the network in this study. Two security gateways GW1 and GW2 are placed at the two boundaries of the unprotected network and provide the link padding necessary to prevent traffic analysis of the payload traffic exchanged between the protected subnets A and B.
Note that the gateways can be realized either as stand-alone boxes, modules on routers or switches, software additions to network stacks, or device drivers at the end hosts. In this paper, we assume that they are stand-alone boxes. Nevertheless, the analysis in this paper is also effective for other implementations. To simplify the discussion, the communication is one-way from Subnet A to Subnet B. Consequently, GW1 and GW2 are also called sender gateway and receiver gateway respectively.
3.2 Link Padding M echanism
The goal of the adversary is to perform traffic analysis and infer critical characteristics of the payload traffic exchanged between protected subnets over the unprotected network. We limit the interest of the adversary to the payload traffic rate, that is, the rate at which payload traffic is exchanged between protected networks. The traffic rate is a piece of important information in many mission-critical communication applications [15]. Specifically, we assume that there is a set of discrete payload traffic rates {w1, ¼, wm }. The rate of payload traffic from the sender may be one of those m rates at a given time. Consequently, the objective of the adversary is to identify at which of the m rates the payload is being sent.
One way to counter the traffic analysis attacks is to ``pad" the payload traffic, that is, to properly insert ``dummy" packets in the payload traffic stream so that the real payload status is camouflaged. There are many possible implementations of link padding algorithms on the two gateways in Figure 1. The most common method uses a timer to control packet sending, and works as follows: (a) On GW1, incoming payload packets from the sender are placed in a queue. (b) An interrupt-driven timer is set up on GW1. When the timer times out, the interrupt processing routine checks if there is a payload packet in the queue: (1) If there are payload packets, one is removed from the queue and transmitted to GW2; (2) Otherwise, a dummy packet is transmitted to GW2.
We need to make a few remarks before we proceed further.
(1) In this paper, we assume that packet contents are perfectly encrypted (e.g., by IPSec with appropriate options) and are thus non-observable. In particular, the adversary cannot distinguish between payload packets and ``dummy" packets used for padding.
(2) It is obvious from the implementation described above, the only tunable parameter is the time interval between timer interrupts. The choice of this parameter discriminates different padding approaches. A system is said to have a constant interval timer (CIT) if the timer is a periodic one, i.e., the interval between two consecutive timer interrupts is constant. This is the most common method used for padding. On the other hand, a system is said to have a variable interval timer (VIT) whenever the interval between two consecutive timer interrupts is a random variable and satisfies some distribution.
As we will see in the later part of this paper, CIT and VIT systems may perform significantly differently in preventing traffic analysis attacks.
(3) We assume that all packets have a constant size. Thus, observing the packet size will not provide any useful information to the adversary. The only information available for the adversary to observe and analyze is the timing of packets. This assumption should simplify the discussion without loss of the generality. See [7] for a discussion on how to extend our results in this paper to the case where packets may have variable sizes.
3.3 Adversary Strategies
Recall that we assume that the objective of the adversary is to identify at which of the m possible rates the payload is being sent, and the adversary limits himself to passive attacks, i.e., observations of the traffic. In addition, the adversary's access to the system is limited to the unprotected networks. The protected subnets and hosts within are not accessible. Neither is the link padding infrastructure. This means that, in Figure 1, the adversary can only tap somewhere between gateways GW1 and GW2.
We also assume that the adversary has complete knowledge about the gateway machines and the countermeasure algorithms used for preventing traffic analysis. For example, the adversary can simulate the whole system, including the gateway machines, to obtain a priori knowledge about traffic behavior. In many studies on information security, it is a convention that we make worst-case assumptions like this.
Based on these assumptions, the adversary can deploy a strategy based on Bayes decision theory [4]. The entire attack strategy consists of two parts: Off-line training and run-time classification. We now describe them below.
Off-line training The off-line training part can be decomposed into the following steps:
(1) The adversary selects a statistical feature of the Packet Inter-Arrival Time (PIAT) that will be used for traffic rate classification. Possible features we study in this paper are sample mean, sample variance, and sample entropy.
(2) The adversary reconstructs the entire link padding system and collects timing inforamtion at different payload traffic rates. From this information, the adversary derives the Probability Density Functions (PDF) of the selected statistical feature. As histograms are usually too coarse for the distribution estimation, we assume that the adversary uses the Gaussian kernel estimator of PDF [17], which is effective in our problem domain.
(3) Based on the PDFs of statistical features for different payload traffic rates, Bayes decision rules are derived. Recall that there are m possible payload traffic rates w1, ¼, wm . The Bayes decision rule can be stated as follows:
The sample represented by feature s corresponds to payload rate wi if
|
|
for all j = 1, ¼, m.
Here P(wi) is the a priori probability that the payload traffic is sent at rate wi, and P(wi|s) is the post priori probability that the payload traffic is sent at rate wi when the collected sample has the measured feature s.
Run-time Classifcation Once the adversary completes its training phase, he can start the classification at run time. We assume the adversary uses some means to tap the network between gateways GW1 and GW2. In particular, when he wants to determine the current payload rate, the adversary collects a sample of packet inter-arrival times. He calculates the value of the statistical feature from the collected sample, and then uses the Bayes decision rules derived in the training phase to match the collected sample to one of the previously defined payload traffic rates.
4 Derivation
of Detection Rate
4.1 Overview
4.1.1 Definition of Detection Rate
Given the models described in the previous section, we would like to evaluate the sCalling ghostscript to convert, please wait ... ystem security in terms of detection rate. Detection rate is defined as the probability that the adversary can correctly identify the payload traffic rate. In this section, we derive the closed-form formulae for detection rates when the adversary uses sample mean, sample variance, or sample entropy, as the statistical feature, respectively. Our formulae will be approximate ones due to the complexity of the problem. Nevertheless, these formulae do correctly reflect the impact of various system parameters, including the type of padded traffic, sample size, and statistical feature used. These relationships are extremely useful in design of a link padding system so that the overall detection rate can be minimized. In the next section, we will see that experimental data well matchs the performance predicated by our approximation formulae.
We will focus our discussion on systems with only two payload traffic rates, namely wl as the low traffic rate and wh as the high traffic rate, and assume that both traffic rates occur with equal probability. Extensions on this will be discussed in Section 6.
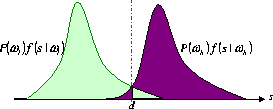
Figure 2: Bayes Decision
Figure 2 shows the PDFs of the statistical features conditioned on two alternative payload traffic rates. Let d be the solution of the equation
|
(3) |
and assume that there is a unique solution to the equation. Consequently, the Bayes decision rule now becomes
|
The error rate for the Bayes decision rule can be calculated as follows:
|
The detection rate is then given by
|
While numerical methods can be applied to calculate the detection rates, for example with the use of (), our goal here is to derive close-form formulae that can reveal the relationship between the detection rate and other system parameters.
4.1.2 Decomposition of Packet Inter-Arrival Time
Recall that the adversary collects a sample of packet inter-arrival time at run time in order to perform the classification. Thus, to derive the detection rate, we need to formally model the packet inter-arrival time. For a given system, let random variable X be the packet inter-arrival time. X can be considered as the sum of three other random variables:
|
where T is the designed interval of two consecutive timer interrupts for the timer, and dgw and dnet reflect the noise added by disturbance in the gateway system and by congestion in the internetwork, respectively.
Note that T is defined by the link padding policy. T is constant for CIT link padding but follows a specific distribution for VIT link padding.
dgw is caused by a number of factors, which may impact the accuracy of the timer's interrupt: (1) First, the context switching from other running process to the timer's interrupt routine may take a random time. (2) Furthermore, a timer interrupt may be temporally blocked due to other activities. For example, if an payload packet from the sender is arriving at the network interface card of the gateway, the network interface card would generate an interrupt request, which can block all the processes including the (scheduled) timer interrupt 1. Thus, the timer's interrupts may be subtly but randomly delayed by incoming payload packets. This implies that the padded traffic's PIAT may be correlated with the payload traffic.
dnet captures the disturbance on the padded traffic's PIAT caused by crossover traffic at routers and switches. Clearly, dnet depends on the position at which the adversary collects its sample. If the collection is done right at the output of the sender gateway, this noise may be ignored. However, if the adversary collects its sample far away from the sender gateway, the noise level can be high as crossover traffic may significantly interfere with the padded traffic.
In this paper, we assume that both T, dgw and dnet are normally distributed. These assumptions simplify analysis without loss of generality and will be validated by our experiments in Section 5. Specifically,
|
(9) |
where sT2 = 0 in the case of CIT link padding. And
|
(10) |
where snet2 = 0 when the adversary observes the padded traffic at a position next to the sender's gateway GW1. Similarly
|
(11) |
As dgw may be correlated to the payload traffic, we denote sgw, l2 and sgw, h2 as the variances of dgw when the payload traffic rate is low and high, respectively. Consequently, we denote Xl and Xh are random variable X when the payload traffic rate is low and high, respectively. Thus,
|
(12) |
|
Similarly,
|
|
Here we assume that Xl and Xh have the same mean. This assumption will be validated by our experiments later.
For the convenience of the discussion in the rest of this paper, we need to introduce the ratio
|
where sT2, snet2, sgw,l2 and sgw,h2 are defined in (9), (10), (13), and (15), respectively. The use of r will become clear when we derive the formulae for detection rates for three different statistical features, namely, sample mean, sample variance, and sample entropy.
4.2 The Case of Sample M ean
Let { X1, X2, ¼, Xn } be a random sample of packet inter-arrival times. The sample mean is the average of the elements in the sample:
|
Note that sample mean [`(X)] is a random variable, and an unbiased estimation of X's mean m.
The following theorem provides a closed-form formula for estimation of detection rate when the adversary uses sample mean as the feature statistic.
Theorem 1 The detection rate by sample mean can be
estimated as follows
|
where r is defined in (16).
The proof of Theorem 1 can be found in the first part of Appendix A in [6]. From Theorem 1 the following observations can be made:
(1) The detection rate in (18) is independent on sample size n. That is, when sample mean is used as feature statistic, changing the sample size has no impact on detection rates.
(2) As shown in the second part of Appendix A in [6], the detection rate v[`(X)] is an increasing function of r, where r ³ 1. That is, the smaller r, the lower the corresponding detection rate. When r = 1, the detection rate reaches 50% - its absolute lower bound. In reality, r = 1 may occur when sT2 is sufficiently large. This corresponds to the case when the VIT padding is used.
4.3 The Case of Sample Variance
Let { X1, X2, ¼, Xn } be a random sample of size n from the distribution of X. The sample variance Y is defined as follows
|
Note that sample variance Y is a random variable, and an unbiased estimation of X's variance.
Recall that sh2 is the variance of padded traffic's PIAT conditioned on the high payload traffic rate and sl2 the variance of padded traffic's PIAT conditioned on the low payload traffic rate. sh2 is slightly larger than sl2, which is validated by our experiments in Section 5. Based on these observations, the following theorem provides a closed-form formula for estimation of detection rate when the adversary uses sample variance as the feature statistic.
Theorem 2 Using sample variance with sample size n
as the classification feature gives rise to an estimated detection rate vY
|
where C is calculated
in (21).
|
and r = [(sh2)/( sl2)] as defined in (16).
The proof of Theorem 2 can be found in the first part of Appendix B in [6]. From Theorem 2 the following observations can be made:
(1) The detection rate vY is an increasing function in terms of sample size n. When n ® ¥, the detection rate is 100%. This means that the payload traffic lasts for a long time at one rate, either low or high, the adversary gets such a sample and may detect the payload traffic rate by sample variance of padded traffic's PIAT.
(2) As shown in the second part of Appendix B in [6], the detection rate vY is an increasing function of r in (16), where r ³ 1. That is, the smaller r, the lower the corresponding detection rate. When r = 1, the detection rate is 50%. This corresponds to the case when VIT padding with sufficiently large sT2. This suggests that although the adversary may use a big size of sample to detect the payload rate by sample variance, using a VIT padding with a large interval variance can make such an attack impossible, since no payload traffic can last very long at a fixed rate in practice and the adversary cannot get a sample big enough.
4.4 The Case of Sample Entropy
While there are many empirical entropy estimators available, it's generally very difficult to get those estimators' PDFs. In this work, we take advantage of the relation between entropy and variance of a normal distribution in order to describe sample entropy's effectiveness as the feature statistic. We will then use an empirical robust histogram-based entropy estimator for our experiments.
The following theorem provides a closed-form formula for estimation of detection rate when the adversary uses sample entropy as the feature statistic.
Theorem 3 Sample
entropy with sample size n has an estimated detection rate v[(H)\tilde]
|
where C[(H)\tilde]
is calculated in (23)
|
and r = [(sh2)/( sl2)] as defined in (16).
The proof of Theorem 3 can be found in the first part of Appendix C in [6]. From Theorem 3 we can make a similar set of observations to that of the case of sample variance.
(1) Detection rate v[(H)\tilde] is an increasing function in terms of sample size n.
(2) As shown in the second part of Appendix C in [6], the detection rate v[(H)\tilde] is an increasing function of r in (16), where r ³ 1. When r = 1, the detection rate reaches 50%. In reality, r = 1 may occur when sT2 is sufficiently large. This corresponds to the case when VIT padding with sufficiently large sT2 is used.
From statistical knowledge, we know sample variance is very sensitive to outliers2. In order for empirical estimation of sample entropy to be robust against outliers, we use the method developed in [11]: First, we create a histogram of the PIAT sample for a given bin size (say, Dh). Then, according to [11], the differential entropy estimator of a random variable X's continuous distribution is
|
(24) |
where n is the sample size, ki is the number of sample points in the ith bin, and Dh is the histogram's bin size. If a constant bin size is used throughout the experiment, the term logDh in (24) is a constant and hence does not influence the recognition result. It can therefore be discarded, and the entropy estimation formula simplifies to
|
(25) |
This entropy estimator is robust in the sense that it is based on
probability weighted sum. Generally, outliers have a small probability to
occur. So the probability weight reduces the noise's impact on the entropy
estimation.
5 Evaluations
In this section, we report results on evaluating system security in terms of detection rate. The evaluations will be based on both theoretical analysis (from the previous section) and experiments.
In the experiments, we assume that the adversary uses a high-performance network analyzer, such as Agilent's J6841A [21], to dump the padded traffic for traffic analysis. A series of experiments were carried out: In tCalling ghostscript to convert, please wait ... Calling ghostscript to convert, please wait ... Calling ghostscript to convert, please wait ... erms of padded traffic type, we measure both systems with CIT and VIT padding, In terms of experimental environments, we consider the following cases: a) a laboratory environment, b) a campus network, and c) a wide area network.
GW1 and GW2 in Figure 1 are installed with TimeSys Linux/Real-Time [22]. Both CIT and VIT paddings use a timer with interrupt interval mean equal to 10ms, i.e., E(T) = 10ms with T in (8). The payload has two rate states: 10 packet per second (pps) and 40pps. We assume both rates occur in equal probability, that is, P(wl) = P(wh) = 50% in (7). Note that for such a system with two possible payload traffic rates, the detection rate for the adversary is lower-bounded at 50% corresponding to random guessing.
5.1 Experiments in a Laboratory Environment
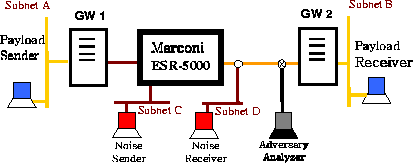
Figure 3: Experiment setup
in laboratory
The advantage of performing the experiments in a laboratory environment is that we can control the cross traffic over the network. The disadvantage is that the generated cross traffic may not have the same characteristics as that in a real network. Nevertheless, our experiment setup is shown in Figure 3.
The two gateways
are connected by a
5.1.1 The Case
of Zero Cross Traffic
For the case of no cross traffic, the workstation in subnet C does not transmit, and the router only deals with the padded traffic from GW1. That is, snet in (16) is 0. Hence, the variance ratio r becomes
|
This situation is a best case for the adversary as he can observe traffic with minimum disturbance. Hence this is the worst-case for us who wants to prevent traffic analysis attacks.
CIT Link Padding
Figure 4: CIT Padding without cross traffic
First, we analyze systems that use CIT link padding. That is, sT2 in (16) is zero. Hence, (26) is further simplified as
|
From the theorems in Section 4, we see that the detection rate is a functions of sample size n and the ratio r.
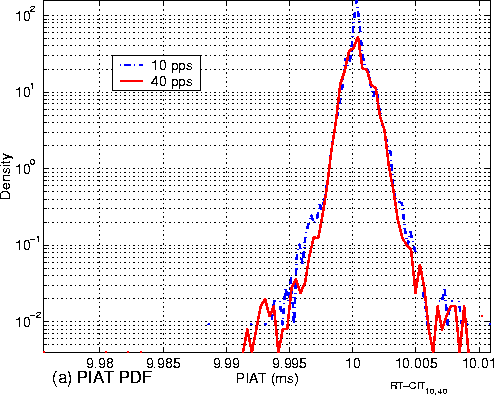
Figure 4 (a) shows the distributions of padded traffic's PIAT under low-rate (10pps) and high-rate (40pps) payload traffic. We have the following observations:
(1) The two distributions are almost bell-shaped. This partially validates our assumption that the padded traffic's PIAT has a normal distribution.
(2) The means of padded traffic's PIAT under different rates of payload traffic are the same. This is also consistent with the assumption made in Section 4.2.
(3) The two distributions are slightly different. The variance of padded traffic's PIAT conditioned on the high-rate payload traffic, sgw, h2 in (15) is slightly larger than the variance of padded traffic's PIAT conditioned on the low-rate payload traffic, sgw, l2 in (13). This implies
|
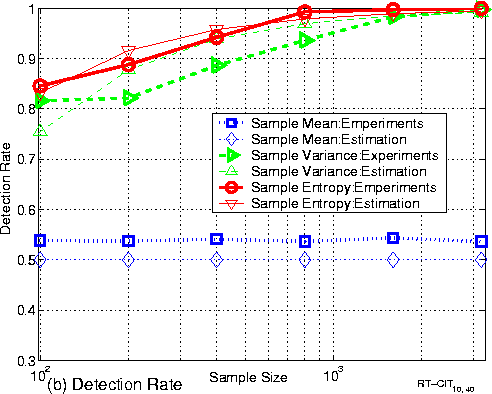
Figure 4 (b) shows both empirical and theoretical curves of detection rate for different feature statistics. We have the following observations:
(1) The empirical detection rate curves coincide well with their theoretical curves. This validates our theories. The empirical detection rate curve of sample variance is a little lower than its theoretical curve because sample variance is very sensitive to outliers in the data.
(2) The detection rate of sample mean is almost 50%. Sample mean is not an effective feature for the adversary.
(3) On the other hand, as the sample size increases, detection rates for both sample variance and sample entropy increase as predicted by our theorems 1 and 3. At sample size of 1,000, both features achieve almost 100% detection rate. This means that CIT padding fails if the adversary uses sample variance or sample entropy as feature statistic. Generally speaking, sample entropy performs empirically better than sample variance in terms of detection rate.
VIT Link Padding
Recall from (26) how the variance ratio r in (16) is given by
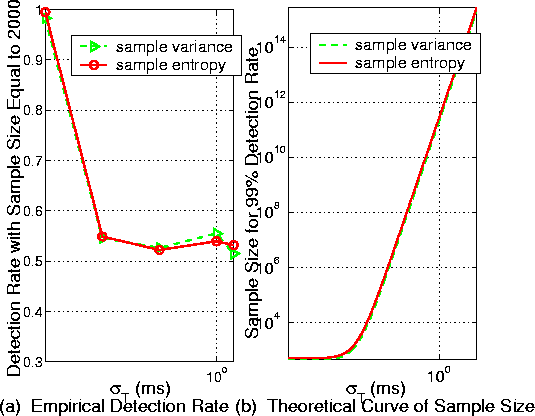
where sT2 ³ 0 since we are using VIT padding. Theorems in Section 4 show that when r approaches 1, the detection rates approach 50% for all the three feature statistics. We note that for CIT padding, the value of r decreases with increasing values of sT2. Figure 5 (a) displays the empirical curves of detection rate in terms of sT for a fixed sample size of 2,000. We can see that when sT increases, the detection rate quickly drops and approaches 50%, as expected. Clearly, a system with VIT padding performs better (i.e., with lower detection rate) than one with CIT padding. Figure 5: VIT padding - detection
rate vs. sample size In any case, as shown in (18) and (22), when the size of sample increases, the detection rate increases as well. An interesting question is: How large a sample has to be in order for the adversary to have sufficient high probability in making a correct detection? Let n(p) be the sample size that can achieve a detection rate of p percent. Figure 5 (b) provides the theoretical curve of n(99%) vs. sT. We can see that with a reasonable value of sT, the sample size needs to be extremely large in order to achieve a 99% detection rate. For example, when the timer interval standard deviation sT = 1ms, to achieve 99% detection rate, the sample size has to be greater than 1011. It is virtually impossible for an attacker to retrieve such a large sample. This clearly shows the effectiveness of VIT padding. 5.2 The Case of Non-Zero
Cross Traffic
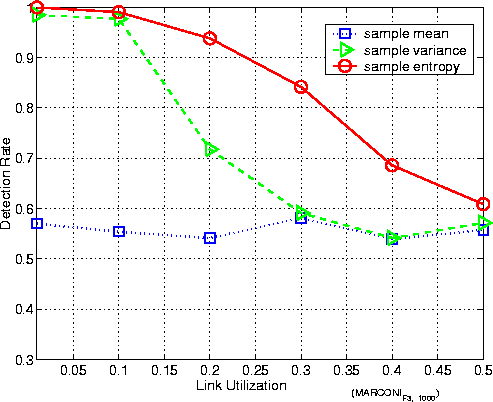
Figure 6: Empirical detection rate with cross traffic in laboratory Recall that the case of zero cross traffic is the best case for the adversary. As VIT has shown to be effective in the case of zero cross traffic, we will no longer have to consider systems with VIT padding here since VIT has been shown to be effective even for the adversary's best-case scenario (zero cross-traffic with a line tap very near the sender gateway). We thus concentrate on the system with CIT padding. In a system with cross traffic, snet2 in (16) may no longer be zero. As for CIT padding, where sT2 = 0, the variance ratio r in (16) now becomes
We observe that r decreases with increasing snet2, resulting in a low detection rate for all feature statistics. Thus, the bigger snet2, the smaller the detection rate. In the experiments described here, cross traffic generated from in subnet C causes the router's congestion, which in turn affects the observation by the adversary. Figure 6 shows how the detection rate is impacted by the amount of cross traffic. We can make the following observations: (1) Note that the PIAT for the padded traffic is 10ms. Hence, the amount of cross traffic is directly proportional to the utilization of the link shared between Subnet B and Subnet D. The data shows that as the link utilization increases, the detection rate by sample entropy and sample variance decrease. Intuitively, this is because the crossover traffic between Subnet C and Subnet D interferes with the padded traffic between GW1 and GW2, and snet2 increases with the shared link's utilization. The sample mean's detection rate remains low, as expected. (2) We observe that sample entropy results in a better detection rate than sample variance does. It can be perceived that, with the increase of shared link's utilization, outliers have more chance of occurring. Sample variance is much more sensitive to outliers and, hence, it has a low detection rate. (3) Even with the link utilization of 40%, sample entropy still can have about a detection rate of 70%, implying that CIT padding may still not be effective in this kind of situation. 5.3 Experiments over Campus and Wide Area NetworksFigure 7: Experiment setup over campus and wide
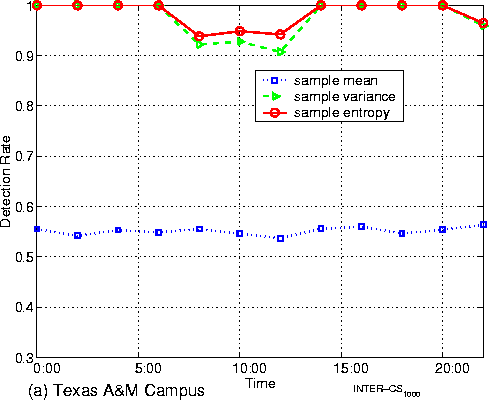
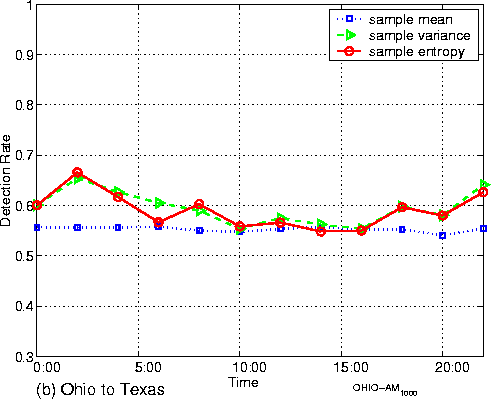
area networks (WAN) Figure 7 shows the setup for the
experiments discussed in this subsections. Figure 7 (a) is a setup for
experiments over the Texas A& Figure
8: Empirical detection rates for experiments over
campus and WAN (sample size=1000) In each case, we
collect data continuously for a complete day (24 hours). The data for the
case of Texas A& Figures 8 (a) and (b) display the detection rate throughout the observation period. We make the following observations: (1)
When the padded traffic traverses just the Texas A& (2)
When the padded traffic traverses more network elements, such as the span of
the Internet between (1) In the case of
wide area networks, sample entropy and sample variance can still get over 65%
detection rates during periods of relatively low network activity (such as at
2:00A 6 Conclusions and Final Remarks
By
statistical analysis of different feature statistics (sample mean, sample
variance and sample entropy) of the padded traffic's packet interarrival times and a lot of experiments, we found
that sample variance and sample entropy can exploit the correlation between
payload traffic rate and packet interarrival times
of padded traffic when the padded traffic is dumped and explored next to the
sender gateway or at a remote site across one or more congested routers. The
reason for CIT padding's failure is that user
traffic causes small disturbances to the timer's interval, which is used to
control packet sending. After a careful analysis, we propose VIT link padding as an alternative to the most common CIT link padding. Both theoretical analysis and empirical results validate the effectiveness of VIT padding strategy. The importance of VIT padding technique is validated by extensive experiments showing that CIT link padding may be compromised even at a remote site behind noisy routers. In this paper we discuss the simple case where two classes of traffic rates should be distinguished. Our technique can be easily extended to multiple ones by performing more off-line training. particular to the environment), the user traffic fitting these distributions can be simulated. This allows the design of link padding schemes that are tuned to this a priori knowledge to prevent traffic analysis. Acknowledgements
We thank Gerry Creager, Nolan Flowers and Xun Wang for the help of setting up the testing enviroment. References
[1] Onion Routing Development Achives. Link padding and the intersection attack. http://archives.seul.org/or/dev/Aug-2002/msg00004.html, 8 2002. [2] P. Baran. On
distributed communications: Ix security, secrecy, and tamper-free
considerations. [3] D. L. Chaum.
Untraceable electronic mail, return addresses, and digital pseudonyms. Communications
of the AC [4] R. O. Duda and P. E. Hart. Pattern Classification. John Wiley & Sons, 2001. [5] Edward W. Felten and [6] [7] [8] S. Ghosh and R. Rajkumar. Resource management of the os network subsystem. Proceedings of the Fifth IEEE International Symposium on Object-Oriented Real-Time Distribute Computing, April 2002. [9] Y. Guan, X. Fu, D. Xuan,
P. U. Shenoy, R. Bettati, and
W. Zhao. Netcamo: Camouflaging network traffic
for qos-guaranteed critical allplications.
In IEEE Transactions on Systems, [10] SafeWeb inc. Safeweb. http://www.safewebinc.com/, 2002. [11] R. [12] R. E. Newman-Wolfe and B. R. Venkatraman. High level prevention of traffic analysis. Computer Security Applications Conference, Seventh Annual, pages 102 -109, 1991. [13] R. E. Newman-Wolfe and B. R. Venkatraman. Performance analysis of a method for high level prevention of traffic analysis. Computer Security Applications Conference, Eighth Annual, pages 123 -130, 1992. [14] [15] J. Raymond. Traffic analysis: Protocols, attacks, design issues and open problems. In H. Federrath, editor, Designing Privacy Enhancing Technologies: Proceedings of International Workshop on Design Issues in Anonymity and Unobservability, volume 2009 of LNCS, pages 10-29. Springer-Verlag, 2001. [16] C. E. Shannon. Communication
theory of secrecy systems. [17] B. W.
Silverman. Density estimation for statistics and data analysis.
Chapman and Hall, [18] D. X. Song, D. Wagner, and X. Tian. Timing analysis of keystrokes and timing attacks on ssh. 10th USENIX Security Symposium, 2001. [19] Qixiang Sun,
Daniel R. Simon, Yi- [20] P. F.
Syverson, D. [21] Agilent
Technologies. Agilent j6841a network analyzer
software. http://onenetworks.comms.agilent.com/NetworkAnalyzer
/J6841A.asp, [22] TimeSys. Timesys linux docs. http://www.timesys.com/index.cfm? hdr=home_header.cfm&bdy=home_bdy_library.cfm, 2003. [23] Brenda Timmerman. a security model for dynamic adaptive traffic masking. New Security Paradigms Workshop, 1997. [24] B. R. Venkatraman and R. E. Newman-Wolfe. Performance analysis of a method for high level prevention of traffic analysis using measurements from a campus network. Computer Security Applications Conference, 10th Annual, pages 288 -297, 1994. [25] V. Voydoc and Footnotes:1 For TimeSys Linux [22] used in our experiments, this request proceeds before the incoming packet reaches the IP layer [8]. From that instant on, the network subsystem in the kernel becomes preemptive. Other high priority tasks such as the timer interrupt routine can then proceed as scheduled. 2 An outlier is an observation that lies an abnormal distance from other values in the sample of the padded traffic PIAT. File
translated from |