An Optimal Strategy for Anonymous Communication Protocols

Yong Guan, Xinwen Fu, Riccardo Bettati, Wei Zhao
Department of Computer Science
Texas A&M University
College Station, TX 77843-3112
E-mail:{yguan, xinwenfu, bettati, zhao}@cs.tamu.edu

1  Introduction

This paper addresses issues related to design and implementation of an optimal strategy for anonymous communications. This optimal strategy is based on a quantitative analysis of the behavior of the anonymous communication systems.

With the rapid growth and public acceptance of the Internet as a means of communication and information dissemination, concerns about privacy and security on the Internet have grown. Anonymity becomes a essential requirement for many on-line Internet applications, such as E-Voting, E-Banking, E-Commerce, and E-Auctions. Anonymity protects the identity of a participant in a networked application. Many anonymous communication systems have been developed, which protect the identity of the participants in various forms: sender anonymity protects the identity of the sender, while receiver anonymity does this for the receiver. Mutual anonymity guarantees that both parties of a communication remain anonymous to each other.

Among these various forms of anonymity, sender anonymity is most critical in many current Internet applications. In E-Voting, for example, a cast vote should not be traceable back to the voter. Similarly, users may generally not want to disclose their identities when visiting web sites. In this paper, we will therefore focus primarily on sender anonymity.

Sender anonymity is most commonly achieved by transmitting a message to its destination through one or more intermediate nodes in order to hide the true identity of the sender. The message thus is effectively rerouted along what is called a rerouting path. In this paper, we study rerouting-based anonymous communication systems in terms of their ability to protect sender anonymity. The selection of rerouting paths is critical for this kind of systems. We study how different path selection strategies affect the ability to protect sender anonymity. For a given anonymous communication system, we measure this ability by determining how much uncertainty this system can provide to hide the true identity of a sender. We call this measure the anonymity degree.

In our investigation, we assume a passive adversary model: The adversary can compromise one or more nodes in the system. An adversary agent at such a compromised node can gather information about messages that traverse the node. If the compromised node is involved in the message rerouting, it can discover and report the immediate predecessor and successor node for each message traversing the compromised node. We assume that the adversary collects all the information from its agents at the compromised nodes and attempts to derive the identity of the sender of a message.

In the following sections, we will elaborate on two observations that we made based on a quantitative analysis of the anonymity degree of systems.

• Common sense indicates that the anonymity degree increases with increasing number of intermediate nodes between the sender and the receiver. (We call this number of intermediate nodes the path length of the rerouting path.) There is a point, however, beyond which increasing the path length actually decreases the anonymity degree. We will give a quantitative analysis of how path length affects the anonymity degree.

• Rerouting schemes give rise to either paths with fixed length (where messages are forwarded to the receiver after traversing a fixed number of intermediate nodes) or variable length (where every intermediate node randomly decides whether to forward the message to the receiver directly or to another intermediate node, for example.). We will show that variable path length strategies perform better than fixed path length strategies in term of anonymity degree. However, when the expected path length is sufficiently large, the difference of anonymity degree is relatively small between different variable and fixed path length strategies.

The remainder of this paper is organized as follows. Section 2 gives an overview of the previous work on anonymous communication systems. In Section 3, we present the system model and discuss the key issues in path selection in such systems. In Section 4, we describe the threat model. In Section 5, we define a security metric, called anonymity degree, to evaluate the anonymity behavior of anonymous communication systems. In Section 6, we report our numerical results. Finally, in Section 7, we present our conclusions.

2  Overview of Anonymous Communication Systems

In this section, we survey the past work related to anonymity, including DC-Net [4,22], Mixes [3,10,11], Anonymizer [1], Anonymous Remailer [2], LPWA [6], Onion Routing [8,17,19,20], Crowds [14], Hordes [15], Freedom [7], and PipeNet [5].

Many existing anonymous communication systems provide various forms of anonymity, such as sender anonymity, receiver anonymity, and mutual anonymity, unlinkability of sender and receiver, or combinations thereof. As mentioned in Section 1, sender anonymity is typically most in demand for current Internet applications.

Systems that provide sender anonymity can be categorized into two classes: rerouting-based systems and non-rerouting-based systems. To the best of our knowledge, DC-Net [4] is the only non-rerouting-based anonymous communication system. In DC-Net, each participant shares secret coin flips with other pairs and announces the parity of the observed flips to all other participants and to the receiver. The total parity should be even, since each flip is announced twice. By incorrectly stating the parity the sender has seen, this causes the total parity to be odd. Thus the sender can send a message to the receiver. The receiver gets the message if it finds that the total parity is odd. Nobody except the sender herself knows who sent it. The advantage of DC-Net over rerouting-based systems is that it does not introduce extra overhead in term of longer rerouting delays and extra amount of rerouting traffic. It relies, however, on an underlying broadcast medium, which comes at great expense as the number of participants increases. Due to this lack of scalability in practice, none of the current on-line applications employs this method. In the remainder of this paper, we will therefore focus on rerouting-based systems.

Most widely-used anonymous communication systems reroute messages through a series of intermediate nodes: The sender sends the message to such an intermediate node first. This node then forwards the message either to the receiver, or to another intermediate node, which then forwards the message again. Once the message traverses the first intermediate node, the sender cannot be identified solely based on the information kept in the header of the message alone. Even though rerouting introduces extra delay and typically increases the amount of traffic due to longer routes, this approach is scalable and practical when such overheads are within tolerable limits. In the following, we will briefly overview a number of such communication systems. They differ from each other mainly by the way the rerouting path is selected. We will therefore categorize them according to their path selection strategies.

Anonymizer [1] provides fast, anonymous, interactive communication services. Anonymizer in this approach is essentially a web proxy that filters out the identifying headers and source addresses from web client requests. Instead of a user's true identity, a web server can only learn the identity of the Anonymizer Server. In this approach, all rerouting paths have a single intermediate node, which is the Anonymizer Server. Similar to Anonymizer, Lucent Personalized Web Assistant [6] also uses the rerouting path with only one intermediate node.

Anonymous Remailer [2] is mainly used for email anonymity. It employs rerouting of an email through a sequence of mail remailers and then to the recipient such that the true origin of the email can be hidden.

Onion-routing [8,17,20,19] provides anonymous Internet connection services. It builds a rerouting path within a network of onion routers, which in turn are similar to real-time Chaum Mixes [3]. A Mix is a store-and-forward device that accepts a number of fixed-length messages from different sources, discards repeats, performs a cryptographic transformation on the messages, and then outputs the message to the next destination in an order not predictable from the order of inputs. A Mix based approach then sends messages over a series of independent such mixes.

Onion Routing I [17,20,19] uses a network of five Onion Routing nodes operating at the Naval Research Laboratory. It forces a fixed length (five hops) for all routes.

Onion Routing II [19] can support a network of up to 50 core Onion Routers. For each rerouting path through an onion routing network, each hop is chosen at random. Rerouting paths may contain cycles. The path selection approach is borrowed from Crowds [14], and the expected route length is completely determined by the weight of flipping a coin.

Crowds [14] aims at protecting the users' web-browsing anonymity. Like Onion Routing, the Crowds protocol uses a series of cooperating proxies (called jondos) to maintain anonymity within the group. Unlike Onion Routing, the sender does not determine the entire path. Instead, the path is chosen randomly on a hop-by-hop basis. Cycles are allowed on the path. Once a path is chosen, it is used for all the anonymous communication from the sender to the receiver within a 24-hour period. At some specific time instant, new members can join the crowd and new paths can be formed.

Freedom Network [7] also aims at providing anonymity for web browsing. Freedom is similar to Onion Routing. It consists of a set of proxies that run on top of the existing Internet infrastructure. To communicate with a web server, the user first selects a sequence of proxies to form a rerouting path, and then uses this path to forward the requests to its destination. The Freedom Route Creation Protocol allows the sender to randomly choose the path, but the path length is fixed at three intermediate nodes [21]. The Freedom client user interface does not allow the user to specify a path containing cycles.

Hordes [15] employs multiple jondos similar to those used in the Crowds protocol to anonymously route a packet towards the receiver. It uses multicast services, however, to anonymously route the reply back to the sender instead of using the reverse path of the request. Similar to Crowds, Hordes also allows cycles on the forwarding path.

PipeNet [5] is a simple anonymous protocol. It is based on the idea of virtual link encryption. Before the sender starts to send the data, it establishes a rerouting path. PipeNet always generates a rerouting path with three or four intermediate nodes.

3  System Model and Path Selection

The system model used in the following discussion is an abstraction of the systems mentioned above. It will therefore lend itself well to discussing the key issues in rerouting-based anonymous communication systems.

3.1  System Model

A rerouting-based anonymous communication system consists of a set of N nodes V = {v_i: 0 £ i < N }, which collaborate with each other to achieve anonymity. Following general practice, we assume that the receiver R is always compromised and we therefore do not include it to be part of the N nodes. For our purposes, we model the network at the transport layer and assume that every host can communicate with every other host. The network therefore can be modeled as a clique. An edge in this graph represents a direct path (i.e., with no intermediate nodes) from a source host to a destination host (possibly through some routers in the network). To hide the true identity of the sender, the message is transmitted from source to destination through one or mCalling ghostscript to convert, please wait ... ore intermediate nodes. We call the path traversed by the message, rerouting path, describe it as follows:

Figure 1: System Model

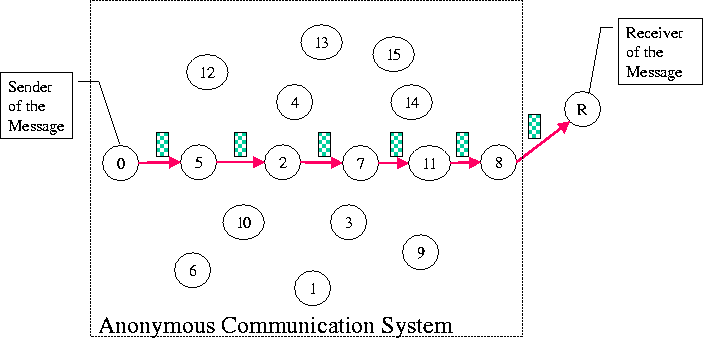
Figure 1 shows a system of 16 nodes, and Node 0 is the sender of a message. The message is transmitted along the rerouting path < 0,5,2,7,11,8,R > determined by the anonymous communication system, and finally arrives at Node R. In this example, the message has traversed 5 intermediate nodes. We define the path length to be the number of intermediate nodes on the path, and we therefore say that the path length is 5 in this case.

3.2  Path Selection

Either before or during the transmission of a message, the rerouting-based anonymous communication system must construct a rerouting path from the source to the destination. Figure 2 shows a framework for how this can be done. (The steps in Figure 2 are often made only implicitly in real systems. For example, the protocol may impose a path length of a given fixed size, and a limited number of rerouting nodes may make a selection of a rerouting sequence irrelevant.)

From Figure 2, it is clear that the key steps in path selection are (1) to choose the length of the rerouting path (path length) and (2) to choose the sequence of intermediate nodes on the path.

There are two kinds of strategies that can be used: fixed length and variable length. In the case of variable length, the path length is a random variable conforming to a specific probability distribution. Onion-Routing I and Freedom use fixed-length strategies, whereas Crowds and Onion-Routing II use variable-length strategies.

It is up to the system developer to decide the type of path length selection (fixed or variable) and its parameters. Since the fixed-length strategy can be regarded as a special case of variable-length strategy, we will focus on the variable path length case in the remainder of this paper.

Once the path length is defined, the rerouting path is chosen by randomly selecting intermediate nodes. Depending on whether a node can be chosen on a rerouting path more than once, we classify paths either as simple paths (no cycle is allowed) or complicated paths (cycles are allowed). Comparing to path length selection, choosing intermediate nodes is rather straightforward when the underlying topology is a clique. So in this paper, we will focus on path lengths. In particular, we study path length distributions that maximize the degree of anonymity of these systems.

4  Threat Model

In this section, we first define the adversary's capabilities in terms of a threat model. We then describe how the adversary can take advantage of these capabilities to monitor the network activities, and use the collected information to derive the probability that each node is the sender of a message.

In this paper, we consider a passive adversary model: By passively monitoring messages in transit, the adversary collects information and derives the probability that a node in the system can be identified as the sender of a message. In order to have access to messages, the adversary has previously compromised a number of nodes. We assume that an anonymous communication system consists of N nodes, of which M are compromised {C_k:1 £ k £ M, C_k Î V }. We assume that the receiver is compromised as well¹. An agent of the adversary at a compromised node observes and collects all the information in the message and so reports the immediate predecessor and successor node for each message traversing the compromised node. We assume that the adversary collects this information from all the compromised nodes and uses it to derive the probability that each node can be identified as the true sender.

Our analysis is based on the worst case assumption in the following sense:

• The sender has no information about number and identities of compromised nodes. The route selection therefore does not rely on knowledge about which nodes are compromised. Thus, some compromised nodes may be on the rerouting path.

• The adversary has full knowledge of the path selection algorithm. In particular, the adversary knows the path length distribution.

• To simplify our discussion, without loss of much generality, we assume that messages that traverse these compromised nodes on the path can be correlated. That is, a message A received by a compromised node can be determined whether it is same as the one A^¢ received by another compromised node on the path at an earlier time. For some anonymous communication systems, for example, Crowds, this is possible by comparing the payload no matter whether it is encrypted or not. For more complicate cases in which the messages can not be definitely correlated, for example, Onion-Routing and other MIX-type systems, we believe that correlation between messages (e.g., probability that messages A and A^¢ are the same one) can be analyzed even if messages can not be completely correlated. We will leave it as our future work.

In previous studies of anonymous communication systems, various attack models were assumed [14,15,19]. As it turns out, many of these models are special cases of our model described above. For example:

• Attack by observing respondent [15] and end server [14]: These two cases correspond to the case in our model where the receiver is compromised.

• Attack by active and passive path traceback [15] and collaborating jondos [14]: These two examples correspond to the case in our model where the rerouting path can be reconstructed by the attacker using the routing information or other monitoring information from at least é^L/₂ ù nodes on the rerouting path compromised (L is the path length).

• Attack by local eavesdropper [14,15]: This corresponds to the case in our model that the sender of the message is compromised.

First of all, the adversary collects the information about the path selection algorithm and its parameters, and all the information about network activities from those compromised nodes. The information collected by the adversary can be classified into two types: static (off-line) information and dynamic (on-line) information. Static information includes the knowledge about the path selection algorithm and its parameters, especially the path length distribution. Dynamic information is collected at run-time and is based on network activities, e.g., when and where messages come from and go to.

Dynamic information is collected by the compromised nodes in the system as follows: every compromised node on the path, say Node C_i, reports the following tuple

Following this, the adversary attempts to derive the probability that each node in the system is the true sender, i.e.,

How to calculate Pr{S = v|F = w} can be found in [9].

5  Measurement and Optimization of Anonymity Degree

In this section, we first define a metric, anonymity degree, to evaluate the ability of anonymous communication systems to protect the identity of a sender. We then describe how to compute the anonymity degree of a system and present the analytical results for a number of special cases. Based on these, we formalize an optimization problem to determine a path length distribution that maximizes the anonymity degree of a system.

5.1  Anonymity Degree

For each node v Î V, the probability Pr{ S = v|F = w} indicates how likely Node v can be identified as the true sender given that the adversary has collected information w (i.e., the tuple sequence given in Section 4).

We assume that, from the adversary's perspective, all nodes have the same a priori probability of being the sender before the collected information can be evaluated. With the additional collected information w, the adversary can derive a more accurate a posteriori probability that nodes can be the true sender.

To evaluate the overall average uncertainty of each node being the true sender given the additional collected information w, we need to define a single value measure on the anonymity that a system can provide. Following Shannon's measure of information, we can define the entropy H(S|F = w) over Pr{S = v|F = w} as follows:

H(S|F = w) gives a precise measurement on the anonymity. When H(S|F = w) is larger, there is greater uncertainty about which of the nodes is the true sender. It has the upper bound log₂ N, which corresponds to the case that there is no compromised node in the system and thus the adversary has no knowledge about what is going on in the system (i.e., each node has equal probability ¹/_N of being the sender). On the other hand, H(S|F = w) has lower bound 0, which means that some node in the system has been identified as the true sender.

By now, considering a given event w (Here, event is a set of experiments whose outcomes (i.e., paths created by the sender) conform to collected information w.), one can use H(S|F = w) to measure the average uncertainty that each node in the system can be identified as the true sender. For an anonymous communication systems, there might be multiple different events the adversary may observe.

Considering all the possible events, we define the anonymity degree H^*(S) of an anonymous communication system as follows:

where

and H(S|F = w) is calculated in Formula (4). Here we assume that the variable path length conforms to the probability distribution Pr{ L = l }, where 0 £ a £ l £ b and a and b are lower and upper bounds on the path lengths, respectively.

The anonymity degree H^*(S) defined in Formula (5) represents the overall average anonymity in the system and will be used as a system security metric in the following.

5.2  Computation of Anonymity Degree H^*(S)

From the definition of anonymity degree in Formula 5, we have to calculate H(S|F = w) and Pr{F = w} for each event w Î W. Here W is the set of all possible events the adversary may observe.

While Pr{F = w} can be easily derived by appropriately partitioning the event space, the computation of H(S|F = w) is not straightforward. Pr{S = v|F = w} for each node v Î V must be calculated. By the law of total probability, for each node v Î V, Pr{S = v|F = w} is given by

where

for a £ l^¢ £ b.

The derivation of Pr{S = v|F = w, L^¢ = l^¢} can be found in [9].

5.3  Analytical Result for Special Cases

In Section 5.2, we have derived the general results for computing anonymity degree. Here, we analyze three special cases that allow for closed-form formulas. While these special cases are simple, the closed-form formulas will help us to analytically verify a number of properties that we observe in the numerical analysis presented in Section 6.

In the first special case, we consider a system using a fixed-length simple path with exactly one compromised node. As discussed in Section 3, we know that L £ N-1. The anonymity degree H^*(S) achieved by this system can be easily determined as follows: For a system having exactly one compromised node and using a fixed-length simple path, when 1 £ N £ 3, we have

When N = 4, we have

When N ³ 5, we have

In the second special case, we consider a system that uses variable-length paths conforming to the following distribution:

In this case, the following theorem can be obtained. For a system that uses variable-length paths with a length distribution conforming to (12), we have

When the path length conforms to the uniform distribution over the interval [a,b] with 3 < a < b, we have

The anonymity degree of a system with a uniform path length distribution over the interval [a,b] with 3 < a < b can be computed as follows:

where l_a = [(a+b)/ 2].

We note that the anonymity degree only depends on the expected value of the path length.

The proofs of the above three theorems can be found in [9].

5.4  Optimization of Anonymity Degree H^*(S)

It is clear that H^*(S) is a function of the path length distribution Pr{L = l}. The goal of this study is to derive an optimal path length distribution that can maximize the anonymity degree of a system. This can be formalized as the following optimization problem:

By solving this optimization problem, we can determine a path length distribution that maximizes the anonymity degree H^*(S).

6  Numerical Analysis

In this section, we focus on analyzing how different path length distributions impact the value of the anonymity degree H^*(S). H^*(S) is numerically computed for systems with different path selection strategies.

Throughout this section, we use N for the number of nodes and M for the number of compromised nodes in the system. We denote by F(l) the fixed-length path selection strategy with paths of fixed length l, whereas U(a,b) is for strategy using paths of variable length that are uniformly distributed over the interval [a,b]. Thus, H^*_F(l) and H^*_U(a,b) stand for anonymity degree of a system using strategy F(l) and U(a,b), respectively.

6.1  Effect of Path Length for Case of Fixed Length Paths

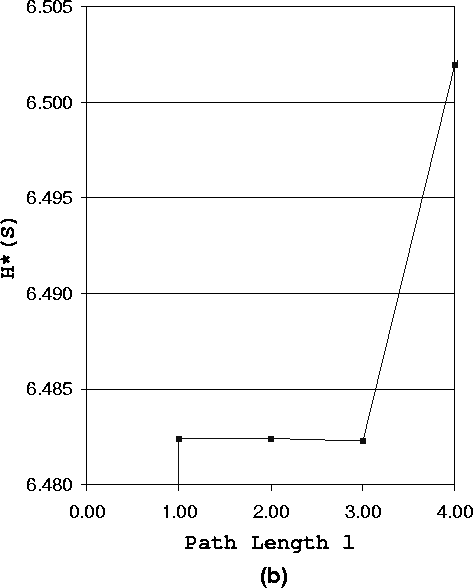
First we study the anonymity degree of a system using fixed length paths. Figure 3 (a) shows how the anonymity degree of the system changes as the path length increases. Figure 3 (b) is a magnified representation of Figure 3 (a) when 1 £ l £ 4.

Figure 3: Anonymity Degree vs. Path Length. (N = 100 and M = 1)

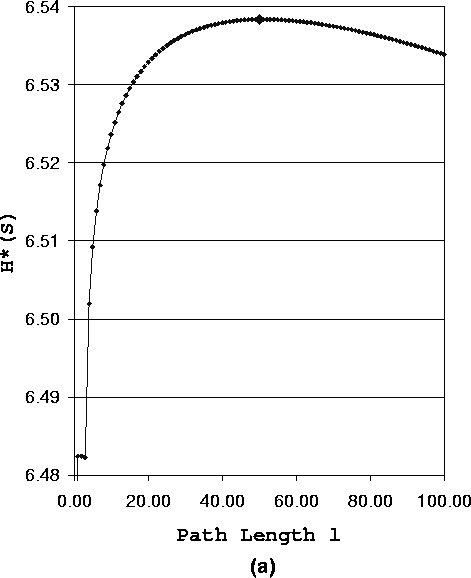
We have the following observations from Figure 3 (a):

• When 3 £ l £ 51, the value of H^*(S) increases as the path length increases. This coincides with general intuition: the more a message is rerouted, the more difficult it is for the adversary to infer the sender.
• However, H^*(S) is not always monotonically increasing as the path length increases. For a system with 100 nodes and 1 compromised node, H^*(S) reaches its maximum value when path length l = 51. When l > 51, H^*(S) becomes a decreasing function. We call this long path effect. This observation is against intuition. One would expect that anonymity would be better with longer paths. Our results show that this is NOT always true. This phenomenon can actually be explained: As the path length increases, the possibility that compromised nodes are on the path increases too. So the adversary would gain better information about the path and his chance to identify the sender is improved. This explains why H^*(S) becomes an decreasing function when l > 51.

Figure 3 (b) shows, when l £ 3, the anonymity degree of the system has a special varying trend. We call this phenomenon short path effect. Short path (l £ 3) increases the chance that the adversary identifies the sender. However, this is NOT always true. From Figure 3 (b), we have the following observations:

• The value H^*_F(4) is larger than that when 1 £ l £ 3. This coincides with general intuition: Length 4 introduces more uncertainty for the cases when the compromised node is the first or second intermediate node on the path. The adversary can not know exactly where the compromised node is on the path.

• For fixed path length 1 and 2, the anonymity degree are identical. Although this contradicts intuition, it can be explained: The main reason for this is that, for both cases of l = 1 and l = 2, the adversary can either know which node is the true sender for sure or know which two nodes can not be the true sender and the nodes other than these two nodes have the same probability of being identified as the true sender. This leads to both path lengths having the same anonymity degree.

• When the path length l is 3, the anonymity degree is worse than that when l = 1 or 2. This can be roughly explained by the fact that, when l = 3, there are more chances that the adversary completely identifies the sender where the receiver and the compromised node cooperate.

Figure 3 (b) does not show H^*_F(0), it is obvious that H^*_F(0) = 0, since a system forwarding the message from the sender directly to the receiver can not have any anonymity, i.e., the sender is exposed to the receiver.

We conclude that, for fixed path length strategy, because of short path effect, the anonymity degree is poor when the path is short. As the path length increases, the adversary has less chance to completely identify the sender and the anonymity degree increases. But because of long path effect, the anonymity degree becomes worse again when the path is too long. For some length, the anonymity degree achieves its optimal value.

6.2  Effect of Path Length Expectation for Case of Variable Length Paths

Figure 4: Anonymity Degree vs. Expectation of Path Length with the Same Path Length Variance. (N = 100 and M = 1)

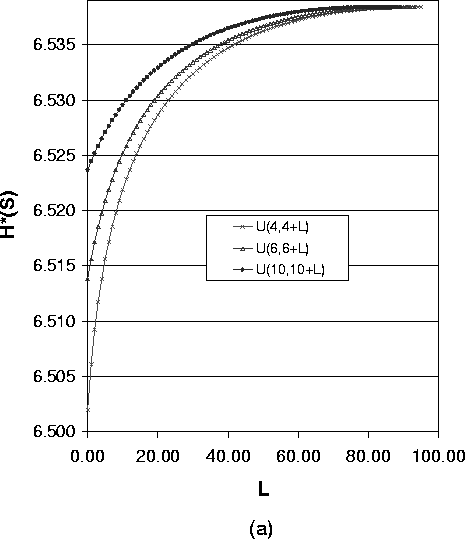
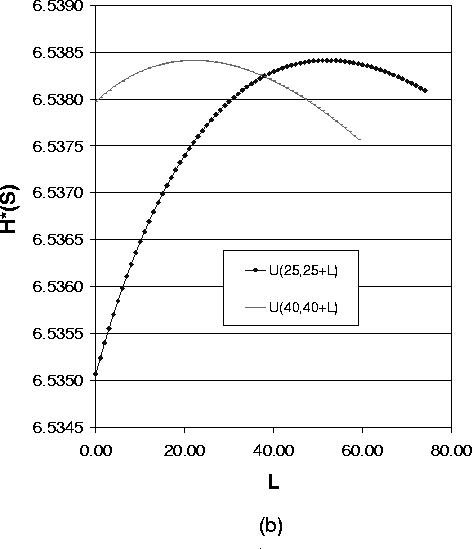
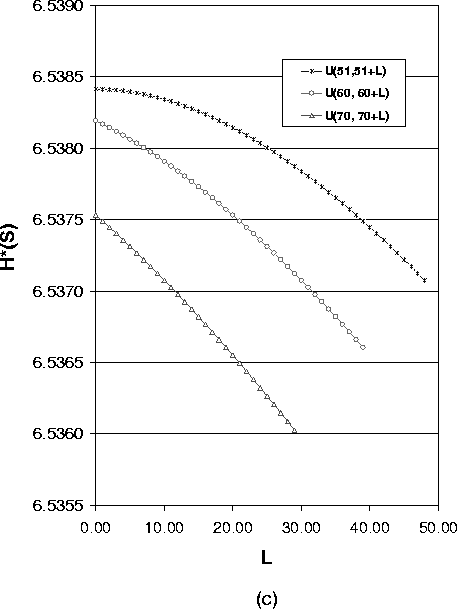
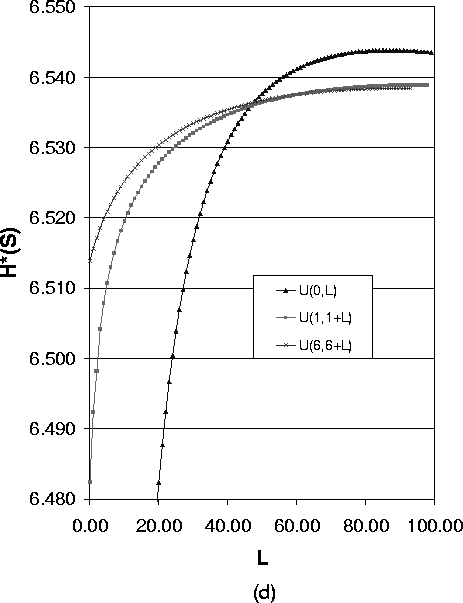
Figure 4 shows how the expected value of the path length impacts the anonymity degree for the case of variable path lengths. We use the uniform distribution U(a,a+L) as the path length distribution, where a is the lower bound of path length and L is the difference between the shortest path and longest path. For a fixed a and a varying L, the value for the anonymity degree describes a curve. Selecting different values for a, we get a group of curves. Then we can compare the anonymity degree for the same L. Here L is an indication of the variance of the uniform distribution.

The four figures in Figure 4 express different meanings:

• For small values of a, the anonymity degree increases as the expected value of path length increases. For the same variance (same L) of different uniform distribution (different a's), the one with bigger expected value of path length (bigger a) has bigger anonymity degree. (Figure 4(a))
• For an intermediate value of a, the anonymity degree has an extreme point. (Figure 4(b))

• For large values of a (a ³ 51), the anonymity degree decreases as the expected value of path length increases. This corresponds to the long path effect in fixed length path selection strategy. For the same variance of different uniform distributions, the one with bigger expected value of path length has smaller anonymity degree. (Figure 4(c))

• This corresponds to the short path effect in fixed length path selection strategy. We can see for the system using distribution U(0,L), due to the use of 0-length path, the anonymity degree is bad when L is small. When L is big, the anonymity degree of the system using distribution U(0,L) gets best anonymity degree. This is partly because of long path effect. That is, with large L, the system using path length distribution other than U(0,L) has more long paths. (Figure 4(d))

6.3  Effect of Path Length Variance for Case of Variable Length Paths

In the following, we show how the variance of path length impacts the anonymity degree. Figure 5 shows the anonymity degree under different path length distributions with the same expected path length.

   


   

Figure 5: Anonymity Degree vs. Variance of Path Length with the Same Expected Path Length. (N = 100 and M = 1)

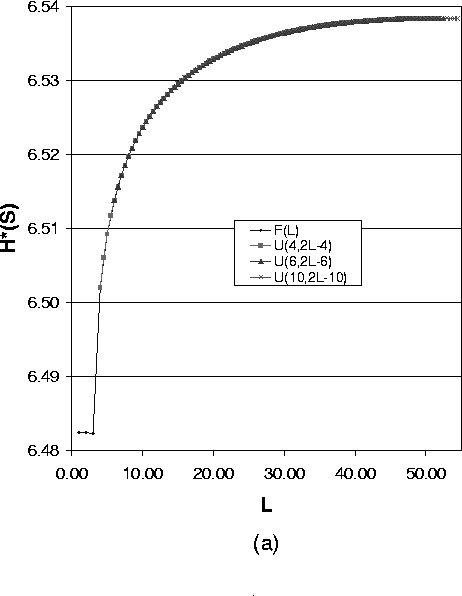
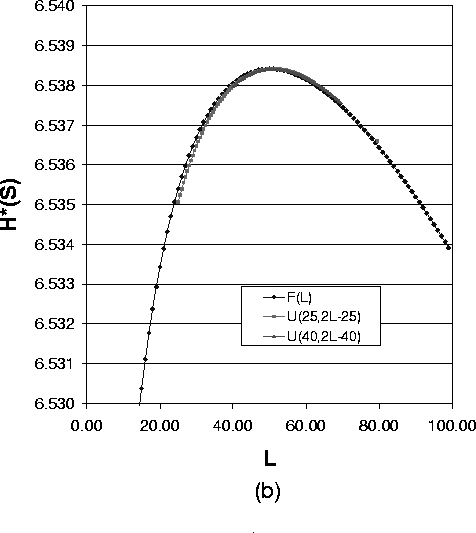
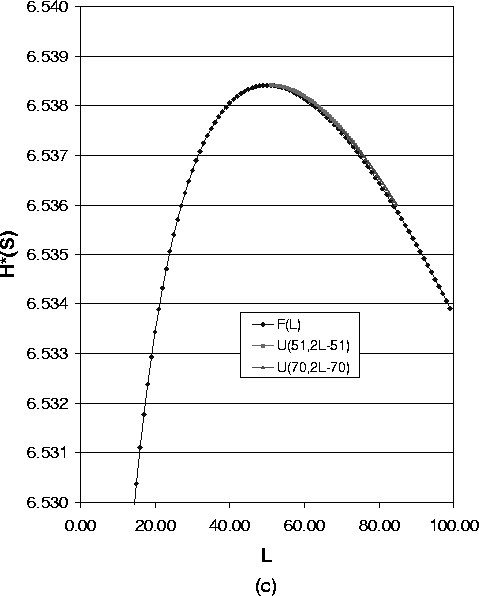
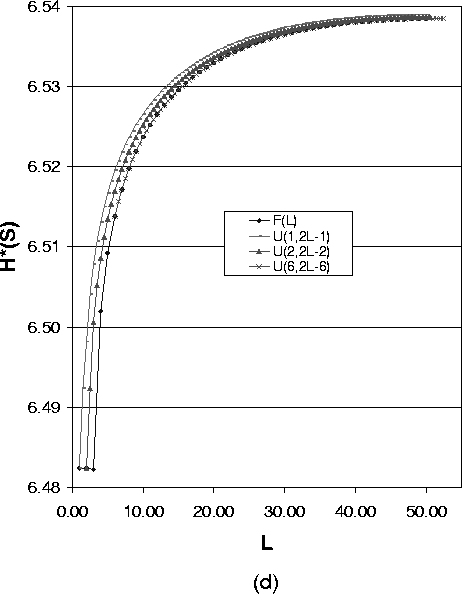
As Formula (14) suggests, Figure 5(a),(b) and (c) show a group of overlayed curves when the uniform distribution lower bound a ³ 3. These figures show that for a system with one compromised node, the expected value of path length of the uniform distribution determines the anonymity degree. So in this case to reduce the implementation overhead, we can just use the fixed length path selection strategy.

Figure 5(d) shows

This is partly because when the expected value of path length is small, the variance plays a more important role on the anonymity degree for different path length distributions.

6.4  Optimal Path Length Distribution

For a given expected path length l, the uniform distribution is described as U(l-d, l+d), where 0 £ d £ min(N-1-l, l). We choose d so that H^*(S) is optimized to achieve maximum value H^o(S), that is

Figure 6: Anonymity Degree vs. Optimal Path Length Distribution. (N = 100 and M = 1)

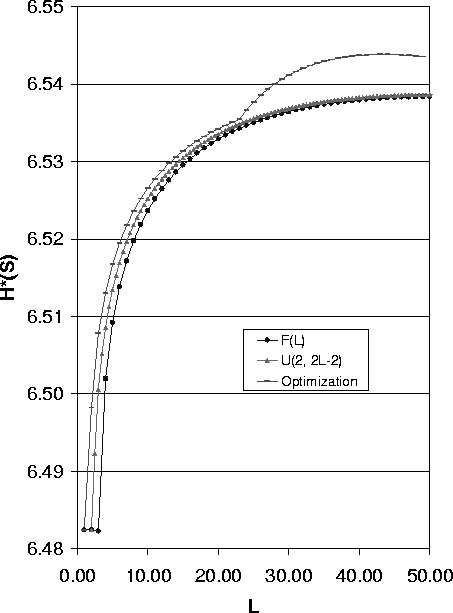
Figure 6 shows the optimization result. The data shows when the expected path length is short, the optimal anonymity degree can be obtained by choosing path length distribution U(1, 2l-1), where l the expected path length. When the expected value of path length is large, the variance plays a more important role and H^o(S|E[L] = l) can be achieved by choosing the distribution U(0, 2l).

We can see that after optimization, the path selection strategy using the optimized path length distribution is better than the strategy using any other uniform distribution and fixed length strategy. Moreover, for the large expected value of path length, the optimal path length distribution gets better anonymity degree.

7  Conclusions

In this paper, we quantitatively analyze the anonymity behavior of anonymous communication systems under different rerouting path selection strategies. We considered several path selection methods used by applications and modeled the behavior of the adversary. We measure the system anonymity in terms of anonymity degree. Our main results from this study are:

1. Long message rerouting path may incur worse anonymity degree. A general intuition has been that the longer the rerouting path, the better the system's anonymity. While this is true in many cases, our analytical result shows that the anonymity of the system may NOT always be improved as path length increases. A longer path of rerouting may not result in a better anonymity.

2. For a system using variable-length paths whose length conforms to a uniform distribution, we find that if the lower bound of the path length is greater than or equal to 3, the strategies using fixed-length paths and variable-length paths conforming to uniform distribution have the same anonymity degree when the path length expectation of uniform distribution is equal to the path length of fixed-length path strategy.

3. Based on our quantitative analysis, we formalize an optimization problem to derive the optimal path length distribution that can maximize the anonymity degree of the system. The optimal path distribution can be computed numerically and analytically.

4. After optimization, variable-length path strategies perform better than fixed-length path strategies in term of anonymity degree. However, no matter what path length strategy is used, the anonymity degree of the system is upper-bounded by log₂ N, where N is the total number of nodes in the system.

Following the analytical results, we can see that several existing anonymous communication systems are not using the best path selection strategy and can be improved to provide higher degrees of anonymity. The results reported in this paper will help system developers properly design path selection algorithms and consequently improve their anonymous communication systems.

References

[1]

The Anonymizer, http:/www.anonymizer.com/.

[2]

Anonymous Remailer, http://www.lcs.mit.edu/research/anonymous.html.

[3]

D. Chaum, Untraceable Electronic Mail, Return Addresses, and Digital Pseudonyms, CACM, v. 24, n. 2, pp. 84-88, 1981.

[4]

D. Chaum, The Dining Cryptographers Problem: Unconditional Sender and Recipient Untraceability, Journal of Cryptology 1/1 (1988), pp. 65-75.

[5]

W. Dai, PipeNet 1.1, http:/www.eskimo.com/ weidai/pipenet.txt.

[6]

E. Gabber, P. B. Gibbons, Y. Matias, and A. Mayer, How to make personalized web browing simple, secure, and anonymous, Proceedings of Financial Cryptography'97-LNCS 1318. Springer-Verlag, 1997.

[7]

I. Goldberg and A. Shostack, Freedom network 1.0 architecture and protocols, http://www.freedom.net/info/freedompapers/index.html, 1999.

[8]

D. Goldschlag, M. Reed, and P. Syverson, Onion Routing for Anonymous and Private Internet Connections, Communications of the ACM, v. 42, n. 2, pp. 39-41, 1999.

[9]

Y. Guan, X. Fu, R. Bettati, and W. Zhao, A Optimal Strategy for Anonymous Communications, Technical Report TR2002-3-1, Dept. of Computer Science, Texas A&M University, November 2001.

[10]

C. Gülcü and G. Tsudik, Mixing Email with Babel, Proceedings of the 1996 Symposium on Network and Distributed System Security, 1996.

[11]

A. Jerichow, J. Müller, A. Pfitamann, B. Pfitzmann, and M. Waidner, Real-Time Mixes: A Bandwidth-Efficient Anonymity Protocol, IEEE Journal on Selected Areas in Communications, v. 16, n. 4, pp. 495-509, 1998.

[12]

Lucent Personalized Web Assistant, http://www.bell-labs.com/projects/lpwa.

[13]

M. Reed, P. Syverson, and D. Goldschlag, Anonymous Connections and Onion Routing, IEEE Journal on Selected Areas in Communications, v. 16, n. 4, pp. 482-494, 1998.

[14]

M. K. Reiter and A. D. Rubin, Crowds: Anonymity for Web Transactions, ACM Transactions on Information and System Security, v. 1, n. 1, pp. 66-92, 1998.

[15]

C. Shields and B. N. Levine, A Protocol for Anonymous Communication Over the Internet, Proceedings of the 7th ACM Conference on Computer and Communication Security, Athens, Greece, Nov. 1-4, 2000.

[16]

V. Scarlata, B.N. Levine, and C. Shields, Responder Anonymity and Anonymous Peer-to-Peer File Sharing, Proceedings of IEEE International Conference on Network Protocols (ICNP) 2001, November 2001.

[17]

P. Syverson, D. Goldschlag, and M. Reed, Anonymous Connections and Onion Routing, Proceedings of the IEEE Symposium on Security and Privacy, Oakland, CA, IEEE CS Press, pp. 44-54, May 1997.

[18]

P. Syverson and S. Stubblebine, Group Principles and the Formalization of Anonymity, World Congress on Formal Methods'99, Toulouse, France, LNCS 1708 Springer-Verlag, pp. 814-833, Sept. 1999.

[19]

P. Syverson, G. Tsudik, M. Reed, and C. Landwehr, Towards an Analysis of Onion Routing Security, Workshop on Design Issues in Anonymity and Unobservability, Berkeley, CA, July 2000.

[20]

P. Syverson, M. Reed, and D. Goldschlag, Onion Routing Access Configuration, DISCEX 2000: Proceedings of the DARPA Information Survivability Conference and Exposition, Hilton Head, SC, IEEE CS Press, pp. 34-40, January 2000.

[21]

Anton Stiglic, Personal Communication, anton@zks.net, Zero-Knowledge Systems Inc., May 2001.

[22]

M. Waidner, Unconditional Sender and Recipient Untraceability in Spite of Active Attacks, Eurocrypt'89, April 1989.

[23]

M. Wright, M. Adler, B. N. Levine, and C. Shields, An Analysis of the Degradation of Anonymous Protocols, Proceedings of ISOC Network and Distributed System Security Symposium (NDSS 2002), February 2002.

[24]

Zero-knowledge Systems, http:/www.zeroknowledge.com/.

¹ This assumption proves true in many realistic situations: For example, an email author may want to hide its identity from the recipient. Similarly, a visitor to a web page may want to hide its identity from the web server.