A Study of
Providing Statistical QoS in a Differentiated Sevices
Network
Shengquan Wang ,
Dong Xuan, Riccardo Bettati, and Wei
Zhao 1
Abstract
In this paper, we propose and analyze a methodology for providing statistical guarantees within the diffserv model in a network, that uses static-priority schedulers. We extend the previous work on statistical delay analysis and develop a method that can be used to derive delay bounds without specific information on flow population. With this new method, we are able to successfully employ a utilization-based admission control approach for flow admission. This approach does not require explicit delay computation at admission time and hence is scalable to large systems. We systematically analyze the performance of our approaches in terms of system utilization. As expected, our experimental data show that statistical services can achieve much higher utilization than deterministic services.
1 Introduction
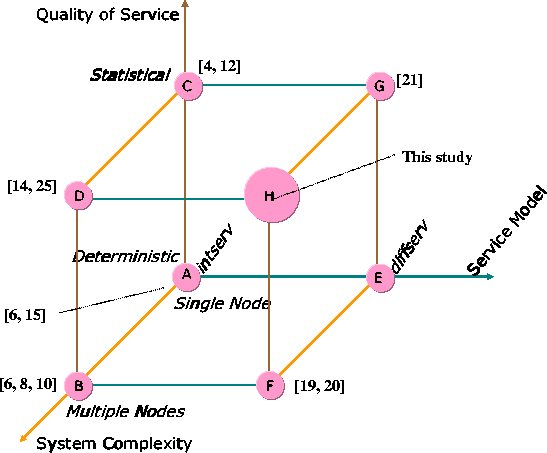
In this paper, we propose and analyze a methodology for providing differentiated services with statistical real-time guarantees in networks that use static-priority schedulers. The problem we address has three dimensions as shown in Fig. 1: Quality of Service, service model, and system complexity, and solutions which have been proposed for different vertices within this space:
Figure 1: Problem Space and
Related Work
Quality of Service: Deterministic guarantees vs statistical guarantees Traditionally, best-effort service has been the main
type of service available over internetworks. While
this type of service has contributed much towards the rapid growth of the
Internet, it cannot effectively support applications that have real-time
requirements.
Service model: Integrated Services vs Differentiated Services One way to provide guaranteed services is to control input traffic by admission control and policing, and to schedule packets based on the requirements of the connection they belong to. A systematic approach based on connection admission control and packet scheduling was proposed within the Integrated Services (intserv) architecture of the IETF [3]. In Integrated Services, connections are controlled both by admission control at connection establishment time and packet scheduling during the lifetime of the connections. Integrated services are difficult to deploy in large-scale high-speed internetworks, as they do not scale well, for two reasons: first, routers are required to maintain status information of flows and schedule packets for large numbers of flows. Second, as the number of flows increases, the run-time overhead incurred for flow establishment and tear-down increases as well. This lack of scalability is, to a large extent, being addressed within the Differentiated Services (diffserv) architecture [2,17]. From the user's point of view, the diffserv model partitions user-level flows into a set of predefined classes. Packets of each class are served in the network according to a class-based scheduling policy. The result is that routers are aware only of aggregations of flows, which are formed from the individual flows at the edge routers. In this fashion, the diffserv model makes the network scalable regardless of the number of flows.
System complexity: single-node network vs multi-node network
Extensive studies have been carried out for various problems in the problem space shown in Fig. 1. For example, for Vertex A which represents the case of providing deterministic services under the intserv model in single-node networks, various solutions have been reported early on [6] and [15]. The case of deterministic services within the intserv model in multi-node networks, represented by Vertex B in Fig. 1, has been covered in [6,8,10]. A number of projects ([4,12]) address the problem associated with Vertex C in Fig. 1, while studies of [14,25] are for the case of Vertex D. For the cases related to Vertex F, solutions have been discussed in [19,20]. The problems associated with statistical services within the diffserv model seem to be particularly challenging. However, a preliminary study for single-node networks has been previously reported in [21]. The work reported in this paper is associated with Vertex H. In this paper, we propose and analyze a methodology for providing statistical guarantees within the diffserv model in multi-node networks. We use Utilization-Based Admission Control (UBAC) to perform scalable admission control. The challenge in using the UBAC method is how to verify the correctness of the utilization bound at the configuration time. The verification has to rely in a delay analysis method. We derive flow-unaware statistical delay formula, which allows us to analyze delays without depending on the dynamic information about flows. We systematically analyze the system performance of our approaches in terms of utilization. As expected, our experimental data show that statistical services can achieve much higher utilization than deterministic services.
The rest of the paper is organized as follows. In Section 2, we discuss previous related work. The underlying network and traffic models for this study are introduced in Section 3. In Section 4, we introduce our proposed architecture for providing statistical services in networks with static-priority scheduling. In Section 5, we develop a delay analysis methodology that is insensitive to flow information. In Section 6, we provide extensive experimental data to illustrate that the utilization achieved within a statistical model is much higher than that of a deterministic model. A summary of the paper is given in Section 7.
2 Previous Works
In this section, we will briefly review the previous work which cover the three dimensions in Fig. 1.
Providing deterministic services within the intserv model (A and B) A lot of studies have been conducted on providing deterministic services within the intserv model both in single-node [15,6] and multi-node [6,8] networks. Under the IntServ model, the work on the single-node network can be relatively easily extended to the multi-node scenario. The main approach is to shape traffic flows at each hops in the network [10]. The nature of awareness about per-flow information under intserv model allows this kind of per-flow shaping. The work in this area mainly focuses on admission control and packet scheduling. With certain traffic models, a number of end-to-end delay calculation methods have been proposed for a large variety of packet scheduling mechanisms [8,18]. Finally, admission control has also been investigated [7,9]. One common limitation of all these systems is their scalability. While they provide deterministic services, they are not scalable to a large internetwork due to their run-time overhead in admission control and packet scheduling.
Providing
deterministic services within the diffserv model (E and F)
Supporting deterministic services within the diffserv model has been addressed in [19] and [20]. Stoica and Zhang [19] suggested to move per-flow information from the core routers to the edge of the network by using packets to carry the flow state information. The result is that the core router does not need to maintain per flow information anymore but infers it based on the information carried with the packet. The expense is additional scheduling overhead at routers and a degree of incompatibility with the traditional IP protocol. In [20], we proposed and analyzed a methodology for providing deterministic services within the diffserv model. We developed a method that can be used to derive delay bounds without specific information on flow population. With this new method, we are able to successfully employ a utilization-based admission control approach for flow admission. This approach does not require explicit delay computation at admission time and hence is scalable to large systems.
Providing statistical services within the intserv model (C and D)
Few have studied on providing statistical services within the diffserv model. [21] conducts a preliminary study for a single-node case. Up to date, there is no study reported to address the issue in the context of the multi-node scenario, which this paper aims to address.
3 Network and Traffic M odels
Our assumptions about network nodes and network traffic follow the Differentiated Services architecture: In the network, we differentiate flow-aware edge routers from core routers, which are only aware of aggregations of flows in form of flow classes. The network traffic consists of flows. We limit our solution to the system with two flow classes. Each flow belongs to one of two flow classes: (1) high-priority class with deadline constraints, i.e., real-time class and (2) a low priority, best-effort class. We proceed below to describe our models in detail.
The IETF diffserv architecture distinguishes two types of routers: Edge routers are located at the boundary of the network, and provide support for traffic policing. Core routers are within the network, and maintain no flow information. Scheduling decisions within the core are therefore made based on class information only. Routers are connected through links, which we assume - for simplicity of argument - to all be of capacity C, in bits per second. When we compute delays, we follow standard practice and model a router as a set of servers, one for each router component where packets can experience delays. Packets are typically queued at some of these servers, typically at the output buffers, where they compete for the output link. Hence, we model a router as a set of output link servers. The other servers (input buffers, non-blocking switch fabric, wires, etc.) are typically not congested, and therefore can be eliminated by appropriately subtracting their constant delays from the deadline requirements of the traffic. We assume that the schedulers in the nodes are not flow aware. Policing and scheduling therefore happen at class level, with class-based static priority schedulers assumed in this paper. Packets belonging to the class with higher priority will be served prior to those with lower priorities.
We call a stream of packets between a sender and receiver a flow. Packets of a flow are transmitted along a single path, which we model as a list of link servers. Following the diffserv architecture, QoS requirements and traffic specifications of flows are defined on a class-by-class basis 2. We assume that at each link server, a certain percentage of bandwidth is reserved for each particular traffic class. Let ak denote the percentage of bandwidth reserved for real-time traffic at Server k. It is the responsibility of the admission control module to ensure that the bandwidth usage of individual classes does not exceed the reserved portion. This is necessary to provide isolation among classes and hence to guarantee end-to-end delays to the flows in each class. We model the traffic arrival for a flow as a stochastic arrival process A = { A(t), t ³ 0}, where random variable A(t) denotes the incoming traffic amount of flows for a link server during time interval [0,t]. The arrival process A is stationary and ergodic. Assume that the traffic arrivals for any two different input links are stochastically independent. The traffic arrival can be bounded either deterministically or stochastically by the arrival traffic envelopes as follows:
Definition 1 [Arrival Traffic Envelope]
Consider a traffic arrival process A = { A(t), t ³ 0}, where random variable A(t) denotes any
incoming flow amount for a link server during time interval [0,t].
- The function b(t) is called the deterministic arrival traffic envelope [6] of the random variable A(t) if A(t+ t) - A(t) £ b(t) for any t > 0 and t > 0;
·
The distribution B(t)
forms the stochastic arrival traffic envelope [13]
of the random variable A(t) if 3
A(t+ t) - A(t)
£ st
B(t) for any t > 0 and t > 0.
A possesses independent and stationary increments, i.e., for any t, t, the random variables A(t+t) - A(t) for different t are mutually independent and possesses the same probability distributions. We use m(t) and RV(t) to describe the mean rate value and rate-variance of [(A(t+ t) - A(t))/ t], respectively. We assume that a real-time traffic flow is controlled at its source router by a leaky bucket with burst size s and average rate r.
4 A QoS Architecture
In this section, we introduce an architecture which is used to provide statistical guaranteed services under the diffserv model in static priority scheduling networks. This architecture consists of three major modules:
Statistical flow-population-insensitive delay computation and utilization bound verification: This module is invoked at configuration time. An ingenious flow-population-insensitive delay method is used to estimate the delay upper bound for every class at each router. This module verifies whether the end-to-end delay bound in each feasible path of the network satisfies the deadline requirement as long as the bandwidth usage on the path is within a pre-defined limit, i.e., the utilization bound.
Efficient admission control: Utilization-based admission control is adopted. As the delay has been verified at configuration time, this module checks only if the bandwidth is available along the path of the new flow.
Packet forwarding control: In a router, packets are transmitted according to their priorities which are marked in their header. Within the same priority, packets are served in FIFO order.
Among the above three modules, the
first module, statistical flow-population-insensitive delay computation and
utilization bound verification, is of most importance. Utilization-based
admission control works around a utilization bound. The
correctness of this utilization bound need to be verified at configuration
time. We propose to realize this critical function in three steps: (i) We first obtain a general delay formula which depends on
dynamic flow information; (ii) We then remove the dependence in the delay
formula to get a statistical flow-population-insensitive delay formula; (iii)
Finally, we verify the correctness of the utilization bound by applying the
statistical flow-population-insensitive delay formula,. Among the above three
steps, Step (iii) is relatively straightforward once we have the statistical
flow-population-insensitive delay formula. We can apply the delay formula to
check, under the given the utilization bound, whether the end-to-end delay
bound in each feasible path satisfies the deadline requirement by the given
probability. In many cases, application system designers would like to know the
5 Statistical Flow-Population-Insensitive Delay Computation
A statistical delay guarantee can be defined as a bound on the delay violation probability, i.e., P{D > d} £ e, where the delay D suffered by a packet is a random variable, d is the given deadline, and e is the given violation probability, which is generally small. We take two steps to perform statistical delay analysis: Per-hop delay analysis and End-to-end delay analysis. The per-hop delay analysis cover the servers at edge and core routers. The per-hop delay will then be used to compute to the end-to-end delay.
5.1 Per-hop Delay Analysis
Since static priority scheduling does not provide flow separation, the local delay at a server depends on information (number and traffic characteristics) of other flows both at the server under consideration and at servers upstream. Therefore, all the flows currently established in the network must be known in order to compute delays. While some formulas could be used (at quite some expense) for flow establishment at system run time, they are not applicable for delay computation during configuration time, as they rely on information about flow population. Fortunately, the following theorem gives a delay violation probability formula without information about flow population. 4
Theorem 1 Consider a
static-priority scheduler with link capacity C such that the real-time traffic
at a given server has an associated deadline d, the delay violation probability
for a random real-time packet at this server is bounded by
|
(1) |
|
and Y is the maximum worst-case delay suffered by the traffic before arriving at the current server. It can be computed by a method in [20]. s0 = s(t), s1 = s(b), where the function s = s(t) can be determined by [1/( [1/( 1-e-s)] - 1/s)] = 1/t([(s)/( r)] + Y), t = [([(s)/( r)]+Y)/( [C/( r)]-1)] and b = [(a)/( 1-a)] ([(s)/( r)]+Y).
Derivation of (1) is discussed in the Appendix. At this point, we would like to make the following observations on Theorem 1: (i) Usually a delay violation probability for a server would depend on the state of the server, i.e., the number of flows that are admitted and pass through the server. We note that (1) is independent from this kind of information, and just depends on s, r, a, C, and Y. The values of these parameters are available at the time when the system is (re-)configured. Hence, the delay computation formula is insensitive to the flow population information. (ii) The right-hand side of (1) can be computed numerically. It is a minimum optimization problem for an explicit function. We define [(s)/( r)] as relative burstiness. The delay formula depends on the relative burstiness [(s)/( r)].
5.2 End-to-end
Delay Analysis
Having derived the delay violation probability formula for the individual hops (servers), in this section, we will study how to perform end-to-end delay analysis. Because of the fact that delays in servers along the route may be correlated to each other, it is difficult to synthesize per-hop delays into the end-to-end delay. One way is to explicitly separate the correlation among the per-hop delays by using policers. With policers, the end-to-end delay will be partitioned into each server along the route, therefore the delays suffered in all servers will be independent. However, heavy overhead will be introduced by policers. Hence, this strategy is not applicable in the diffserv model. Fortunately, in [25], the authors test the hypothesis that per-hop delay distributions are independent of each other. The delay distributions they obtained suggest strong hop-to-hop independence at high link utilization, as evidenced by the fact that the convolution of the delay distributions (which assumes independence of these distributions) is so close to the observed end-to-end distribution.
Our objective of the delay analysis is to get the maximum usable utilization. In general, with the maximum usable utilization, the network will have relatively heavy traffic. Hence, the above hypothesis can be applied into our derivation and the end-to-end delay distribution can be obtained by the convolution of per-hop delay distributions.
6 Experimental Evaluation
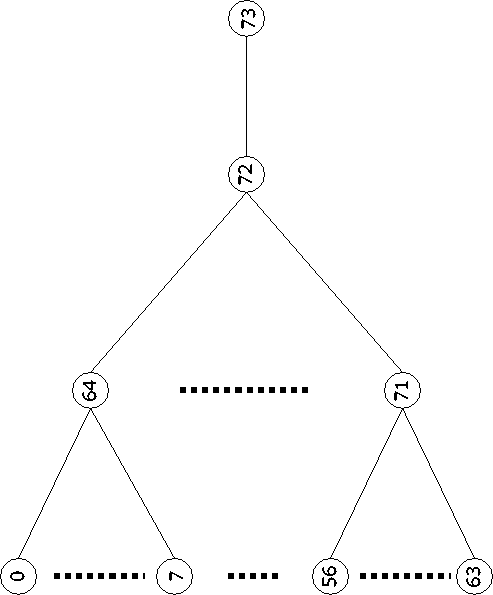
Network and Traffic
Figure 2: The network topology for the
simulation
Performance
Evaluation
In the following, we report performance results and make observations. Due to the limited space, we only present a limited number of cases here. However, we find that the conclusions we draw here generally hold for many other cases we have evaluated.
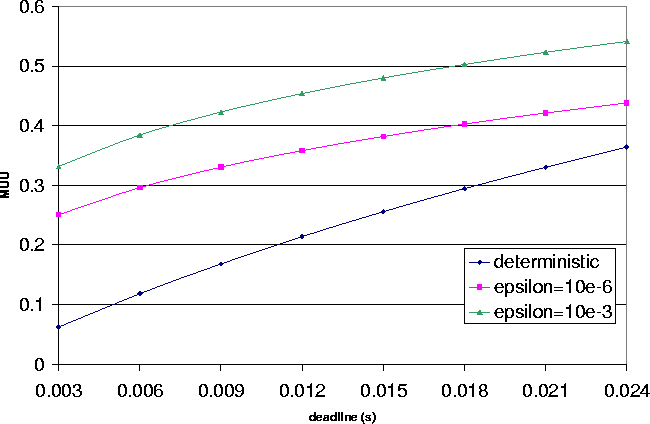
Figure 3: Sensitivity of
Sensitivity
of
Data on sensitivity of utilization
to deadline are given in Fig. 3. From Fig. 3,
we have the following observations: (i) As expected, the utilization for both deterministic and
statistical models increases as the deadline increases. This means that the
higher the deadline, the higher utilization we can get for both deterministic
and statistical models. A longer deadline results in more packets meeting
deadline and, therefore, higher values for the
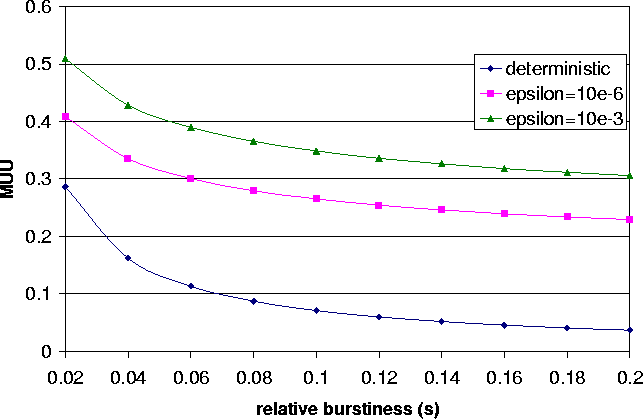
Figure 4: Sensitivity of
Sensitivity
of
From Fig. 4,
we see that the relative burstiness of traffic
heavily impacts on the
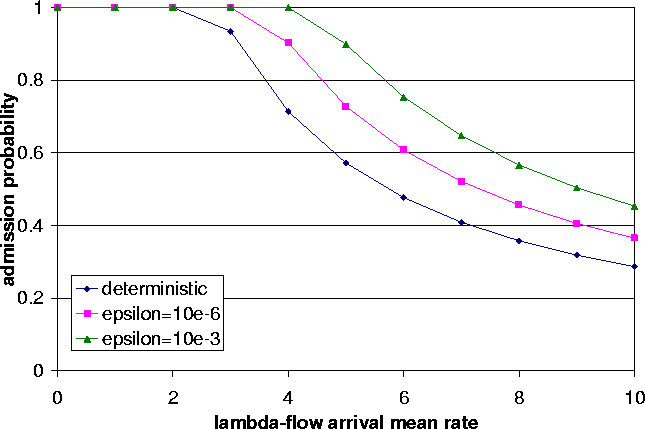
Figure 5: Sensitivity of Admission Probability to Flow
Arrival Rate (d = 20 ms, s = 1280 bits, r = 64K bps, C = 100
Sensitivity of Admission Probability to Flow Arrival
Rate
Data on sensitivity of admission probability are given in Fig. 5. From this figure, we make the following observations: (i) Admission probability is sensitive to the flow arrival rate l for all models. Admission probability decreases as l increases in all models. The reason is obvious: A large l value implies a large number of flow arrivals in the system. Since the bandwidth is limited, some flows are not allowed to enter the network. Therefore, the admission probability decreases. (ii) Different models have different sensitivities to l in terms of admission probability. The statistical models always achieve higher admission probabilities than the deterministic model. Larger delay violation probability (i.e., e) always achieve higher admission probability. This is because of the achievable utilization is proportional to e.
7 Conclusions
In this paper, we have proposed a methodology for providing differentiated services with statistical performance guarantees in networks that use static priority schedulers. Given that static priority schedulers are widely supported by current routers, we believe that our approach is practical and effective to support real-time applications in existing networks. We have used Utilization-based Admission Control (UBAC) approach which requires a configuration-time verification to determine a safe utilization bound of servers. Admission control at runtime then is reduced to simple utilization tests on the servers along the path of the new flow. Hence, the approach is scalable. The verification of the utilization bound is involved with delay analysis. The general delay derivation depends on flow population information, which is not available at the system configuration time. We have extended the general approach and developed a method that allows us to analyze the delays without depending on the dynamic status of flow population.
References
[1]
G.
Agrawal, B. Chen, W. Zhao, and
[2]
S.
Blake, D. Black,
[3]
R.
Braden and D. Clark and
[4]
C.
Chang, Stability, queue length, and delay of deterministic and stochastic queueing networks, IEEE Transactions on Automatic
Control,
[5]
B. Choi and R. Bettati, Endpoint Admission Control: Network Based Approach, Proceedings of IEEE ICDCS, April 2001.
[6]
R. Cruz, A Calculus for Network Delay, Part I & II, IEEE Transactions on Information Theory, Jan. 1991.
[7]
A.
Dailianas and A. Bovopoulis,
Real-time admission control algorithms with delay and loss guarantees in AT
[8]
N.
Figueira, J. Pasquale, An Upper Bound on Delay
for the VirtualClock Service Discipline, IEEE/AC
[9]
V.
Firoiu, J. Kurose, and D. Towsley,
Efficient admission control for EDF schedulers, Proceedings of IEEE
INFOCO
[10]
L.
Georgiadis, R. Guérin, V. Peris, K.N. Sivarajan, Efficient
Network QoS Provisioning Based on per Node Traffic Shaping, IEEE/AC
[11]
E.
Knightly, H-BIND: A new approach to providing statistical performance
guarantees to VBR traffic, Proceedings of IEEE INFOCO
[12]
E.
Knightly, Enforceable quality of service guarantees for bursty traffic
streams, Proceedings of IEEE INFOCO
[13]
J.
Kurose, On computing per-session
performance bounds in high-speed multi-hop computer networks, Proceedings
of AC
[14]
J. Liebeherr, S. Patek and E. Yilmaz, Tradeoffs in Designing Networks with End-to-End Statistical QoS Guarantees, Proceedings of IWQoS, June 2000.
[15]
C.
Liu and J. Layland, Scheduling algorithms for
multiprogramming in a hard real time environment, Journal of AC
[16]
D.
[17]
K. Nicols, V. Jacobson, L. Zhang, A Two-bit Differentiated Services Architecture for the Internet, Internet-Draft, Nov. 1997.
[18]
A.
Parekh and R. Gallager, A
generalized processor sharing aApproach to flow
control in integrated services networks: the single-node case, IEEE/AC
[19]
I.
Stoica, H. Zhang, Providing Guaranteed Services
Without Per Flow
[20]
S.
Wang, D. Xuan, R. Bettati and W. Zhao, Providing
Absolute Differentiated Services for Real-Time Applications in Static Priority
Scheduling Networks, Proceedings of IEEE INFOCO
[21]
S. Wang, D. Xuan, R. Bettati and W. Zhao, Differentiated Services with Statistical Real-Time Guarantees in Static-Priority Scheduling Networks, Proceedings of IEEE RTSS, Dec. 2001.
[22]
D.
Wrege, E. Knightly, H. Zhang, and J. Liebeherr, Deterministic
delay bounds for VBR video in packet-switching networks: Fundamental limits and
practical tradeoffs, IEEE/AC
[23]
T.
Wu and E. Knightly, Enforceable and Efficient Service Provisioning,
Computer Communications Journal: Special Issue on
[24]
S.
Wang, D. Xuan, R. Bettati and W. Zhao, A Study of
Providing Statistical QoS in a Differentiated Sevices
Network, Technical Report, Department of Computer Science, Texas A&
[25]
D.
Yates, J. Kurose, D. Towsley, and
Appendix: Deriving Formula (1)
In the following, we discuss how to derive the formula given in (1). We will start with a formula for delay that depends on flow population, which we call the general delay violation probability formula. We will then describe how to remove its dependency on information of flow population.
The Central Limit Theorem states that the summation of a set of independent random variables converges in distribution to a random variable that has a Normal Distribution. The following lemma is based on this theorem [12]. The general delay violation probability formula is given out by this lemma.
Consider a static priority scheduler with link capacity C such that the real-time traffic at a given server has an associated deadline d. Suppose that the traffic process into the server consists of independent traffic processes Aj, which have stochastic envelope Bj(t) with mean rate mj(t) and rate-variance envelope RVj(t). The delay violation probability for a random real-time packet is approximately bounded by
|
where F(a) is defined in (2)
and b is the busy period bound
for the real-time traffic at this server and is given by
|
(6) |
For this lemma, we make the following observations: (i) All Aj's need to be independent. In this paper, we consider the group of flows from the same input link as one traffic process. In the following, we will use the notation Gj to denote a group of flows from Input Link j and use bj(t), Bj(t), mj(t), and RVj(t) to specify the deterministic arrival traffic envelope, the stochastic arrival traffic envelope, and the rate-variance envelope applied to the group of flows Gj respectively. Since these traffic processes from different input links, they can be assumed to be independent. (ii) The general delay violation probability formula depends on the flow information, i.e., the individual mean rate mj(t), rate-variance RVj(t), and the deterministic envelope bj(t).
In the following, we will describe methods how to compute these parameters and remove the dependency of the delay formula on the flow information 5.
Computation of
Given the deterministic arrival traffic envelope bj(t) of the traffic process Aj, if Aj is ergodic and its long-term average rate rj = limt®¥ [(bj(t))/ t], With the ergodicity of traffic processes, rj is the mean rate mj(t) for the random variable Aj(t). Based on the maximum entropy principle, the maximum entropy estimate of rate-variance is
|
(7) |
|
(8) |
sj can be solved from rj = [1/( [1/( 1-e-sj)] - [1/( sj)])] and rj = [(bj(t))/( rj t)].
From the above lemmas, we note that mj(t) and RVj(t) are determined by the deterministic envelope bj(t). Recall that we assume the source traffic of a flow is controlled by a leaky bucket with burst size s and average rate r. Hence at the first server (usually in some edge router), bj(t) can be obtained. At an intermediate server (usually in some core router), the traffic will be distorted after traffic aggregation, we need to redetermine the deterministic envelope bj(t). Our approach is to use the worst-case delay to bound the deterministic envelope at intermediate servers. For group of flows Gj with nj flows, let Yj be the maximum worst-case delay suffered by traffic through Input Link j before arriving at the current server. Then the deterministic envelope bj(t) = nj min{C t, s+ r(t + Yj)}.
Removing the Dependency on the Flow Information: The per-hop delay violation probability formula depends on the flow population nj and Yj. In the following, we want to remove the specific input link j and the flow population from this formula. (i) Removing the Dependency on Individual Input Link: Recall that Y is the maximum worst-case delay suffered by traffic before arriving at the current server, then the deterministic envelope bj(t) £ nj min{C t, s+ r(t + Y)}. (ii) Removing the Dependency on the Number of Flows on Individual Input Link: As we described earlier, admission control at run-time makes sure that the link utilization allocated to each class of flows is not exceeded. Recall that a is the ratio of the link bandwidth allocated to the real-time traffic. The total number of the real-time flows on all input links åj = 1L nj £ a[C/( r)]. Therefore, we have åj = 1L n2j £ (a[C/( r)])2. Applying them into Lemma 2, we have åj = 1L mj(t) £ åj = 1L nj r £ aC and åj = 1L RVj(t) £ åj = 1L w(t) (nj r)2 £ w(t) (aC)2, where w(t) = 1/s (r2 - 2 r) + r - 1, and s can be solved from r = [1/( [1/( 1-e-s)] - 1/s)] and r = min{[C/( r)], 1/t ([(s)/( r)]+Y)+1}. 6 Apply them into (5), and after some algebraic manipulation, we have the delay violation probability upper-bound:
|
(9) |
where x(t) = [([d/( a)] 1/t + [(1-a)/( a)])/( Ö{w(t)})], and b = [(a)/( 1-a)]([(s)/( r)]+Y). We note that there is an implicit function s = s(t) (with respect to t) in the above formula. If we use s as the parameter, we can obtain an explicit formula as shown in Theorem 1, which makes the computation easy.
Footnotes:
1
This work was partially sponsored by NSF under contract number EIA-0081761, by
DARPA under contract number F30602-99-1-0531, by Texas Higher Education
Coordinating Board under its Advanced Technology Program, and by Ameritech
Fellowship grant.
2 While at network level all flows within the real-time class have identical traffic specifications and QoS requirements, user-level connections with varying bandwidth and burstiness requirements can be established by using more than one flow.
3 X £ st Y means P{X > Z} £ P{Y > Z}.
4 Recall that we limit our solution to systems with two flow classes. We conveniently omit the class index in the following description. Thus, unless otherwise pointed out, all the traffic parameters are referred to real-time traffic class. Since the per-hop delay analysis focuses on one server, without any confusion, in this subsection, we'll omit server index k.
5 All proofs are given in [24].
6 Since r is independent of j, so is w(t).
File translated from
On